Techniklexikon

Zeeman-Effekt

Nach dem niederländischen Physiker P. Zeeman (1865— 1943) benannter Effekt, der beweist, daß der Spin eines Elektrons (Elektronen) mit einem magnetischen (Magnetismus) Drehmoment verbunden ist. Wirkt umgekehrt ein äußeres Magnetfeld auf Atome ein, spalten sich deren Energieniveaus der Hülle (Valenzelektronen) und damit die Spektrallinien auf. Atom- und Molekülphysik, Aufspaltung von Spektrallinien, die von Atomen, die sich in einem homogenen Magnetfeld befinden, emittiert werden. Dieser Effekt wurde im Jahre 1896 vom holländischen Physiker Pieter Zeeman erstmals beobachtet. Lorentz fand eine klassische Erklärung dieses Effektes, nach der jede Spektrallinie eines Atoms in drei Komponenten aufspalten sollte. Dieses Lorentz-Triplett bezeichnete man als normalen Zeeman-Effekt, weil man auch viele Atome fand, deren Spektrallinien in kompliziertere Strukturen aufspalteten, was man – aus rein historischen Gründen – anomalen Zeeman-Effekt nannte. Der anomale Zeeman-Effekt konnte erst mit Hilfe der von Goudsmit und Uhlenbeck 1925 aufgestellten Hypothese des Elektronenspins erklärt werden – dieser Erfolg verhalf der Theorie des Elektronenspins und des damit verbundenen intrinsischen atomaren magnetischen Momentes des Elektrons letztlich zum Durchbruch. Die quantenmechanische Behandlung des Zeeman-Effektes unter Berücksichtigung des Spins des Elektrons zeigte dann, dass der normale Zeeman-Effekt eigentlich ein Spezialfall des anomalen Zeeman-Effektes ist (der anomale Effekt also den Normalfall darstellt), der nur in Systemen mit Gesamtspin S = 0 und in sehr starken Magnetfeldern auftritt. Man beobachtet auch einen Zeeman-Effekt der Hyperfeinstruktur, den Back-Goudsmit-Effekt.

In seiner klassischen Betrachtung des normalen Zeeman-Effektes berücksichtigte Lorentz die Lorentz-Kraft, die das Magnetfeld auf das um den Atomkern kreisende Elektron ausübt:  (2pn_0/1: Winkelgeschwindigkeit des Elektrons ohne/mit Magnetfeld, B: Magnetfeldstärke). Die Lösung dieser Gleichung lautet näherungsweise .

Die Emissionslinien eines Atoms im Magnetfeld sind in Abb. 1 schematisch dargestellt: Betrachtet man das Elektron als Kreisstrom i mit klassischer Abstrahlungscharakteristik, so findet man bei Beobachtungsrichtung senkrecht zur Feldrichtung das Lorentz-Triplett, das aus drei Linien, der unverschobenen Linie bei n₀ und den verschobenen Linien bei , besteht. Bei Beobachtungsrichtung in Feldrichtung findet man nur die beiden verschobenen Linien. Die Polarisation der Linien ist der Abb. 1 zu entnehmen.

In der quantenmechanischen Interpretation zeigt sich, dass der sog. anomale Zeeman-Effekt auf der Wechelwirkung des atomaren magnetischen Moments der Elektronenhülle M mit dem magnetischen Feld B (in z-Richtung), in dem sich das Atom befindet, beruht. Die zusätzliche potentielle Energie  bewirkt, dass sich die Energieniveaus im Atom verschieben, was zu einer Aufspaltung der Spektrallinien führt. Das atomare magnetische Moment des Elektrons setzt sich aus zwei Komponenten zusammen, dem Bahnmoment , das mit dem Bahndrehimpuls verknüpft ist, und dem Spin-Moment , (mit dem g-Faktor des Elektrons, g_S = 2,0023) das vom Elektronenspin herrührt. Ist das Magnetfeld so stark, dass die magnetische Feldenergie höher ist als die Energie der Spin-Bahn-Kopplung, dann entkoppeln die beiden magnetischen Momente des Elektrons und präzedieren unabhängig voneinander um die Magnetfeldrichtung. Im schwachen Magnetfeld koppeln die magnetischen Momente zum elektronischen Gesamtdrehimpuls J, der dann um die Feldlinien präzediert.

Für das Wasserstoffatom lautet der Hamilton-Operator im homogenen Magnetfeld unter Vernachlässigung des quadratischen Terms:

Für die beiden Grenzfälle ergeben sich damit die folgenden Situationen:

1) starkes Magnetfeld: d.h. . Da im Labor nur Magnetfelder im Bereich < 10 T erzeugt werden können, trifft man diese Situation hauptsächlich in astrophysikalischen Umgebungen (Neutronensterne) an. Im starken Magnetfeld sind die magnetischen Momente von Spin (m_s) und Bahn (m_l) entkoppelt und präzedieren unabhängig voneinander um die Richtung der Feldlinien. Die Energieniveaus im Atom betragen E = E_n + m_B B_z (m_l+2m_s) (m_l und m_s sind die Momente in Feldrichtung).

In Abb. 2 ist die Aufspaltung des 1s- und 2p-Niveaus des Wasserstoffatoms im starken Magnetfeld mit den erlaubten optischen Übergängen dargestellt. Die (2p-1s) Resonanzlinie spaltet hier wie beim normalen Zeeman-Effekt wieder in ein Triplett auf. Dieser Effekt wird Paschen-Back-Effekt genannt.

2) schwaches Magnetfeld: . Hier koppelt der elektronische Gesamtdrehimpuls J mit dem äusseren Magnetfeld. Die Addition von Spin-und Bahndrehimpuls ist im Landéschen g-Faktor g_J berücksichtigt, und die Lage der Energieniveaus im Atom ist E = E_n + E_FS + g_Jm_BB_zm_J.

Abb. 3 zeigt die Aufspaltung der 1s_{1 / 2}- und 2p_{1 / 2}-, 2p_{3 / 2}-Energieterme im Wasserstoffatom. Die zugehörigen Spektrallinien zeigen ein komplizierteres Aufspaltungsmuster als das Lorentz-Triplett.

In diesen Grenzfällen, in denen eine der beiden Kopplungsenergien überwiegt, sind die Verschiebungungen des Energieniveaus symmetrisch zur unverschobenen Linie. Der dazwischen liegende intermediäre Bereich ist theoretisch wie experimentell schwierig zu analysieren (siehe Abb. 4).

Ein weiterer Spezialfall ist der quadratische Zeeman-Effekt, bei dem ist die Verschiebung der Energieniveaus proportional zum Quadrat der Magnetfeldstärke ist und den man bei hochangeregten Zuständen oder in sehr starken Magnetfeldern beobachtet. Der quadratische Term resultiert nicht, wie beim Stark-Effekt, aus einer Störungsrechnung zweiter Ordnung, sondern aus der Struktur des Hamilton-Operators selbst, den man aus der klassischen Hamilton-Funktion eines Teilchens mit Masse m und Ladung q im Vektor- und Skalarpotential

nach Transformation der klassischen Grössen in quantenmechanische Operatoren erhält (unter Berücksichtigung der Relation  für homogene Magnetfelder) :

Der lineare Term in B führt zum anomalen (und normalen) Zeeman-Effekt. Den quadratischen Zeeman-Effekt beobachtet man dann, wenn man den quadratischen Term im Hamilton-Operator nicht mehr vernachlässigen kann, wie es bei hochangeregten Zuständen oder in sehr starken Magnetfeldern der Fall ist.

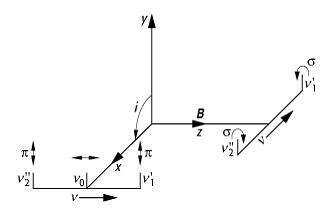
Zeeman-Effekt 1: Klassische Interpretation des normalen Zeeman-Effekts. Das Elektron im Magnetfeld bewegt sich auf einer Kreisbahn und erzeugt den Kreisstrom i, dessen Abstrahlungscharakteristik zu zwei zirkular polarisierten Emissionslinien (s) in Magnetfeldrichtung und drei linear polarisierten Emissionslinien (p) senkrecht zur Magnetfeldrichtung führt.

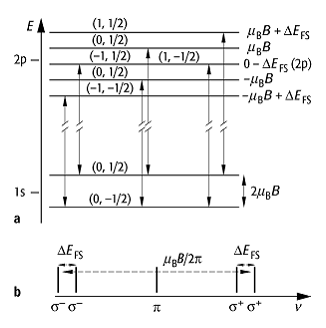
Zeeman-Effekt 2: a) Aufspaltung des 1s- und des 2p-Niveaus des Wasserstoffatoms im starken Magnetfeld mit den erlaubten optischen Übergängen. Im Gegensatz zum klassischen Fall bewirkt die Feinstruktur eine zusätzliche Verschiebung DE_FS der Energieterme mit , die aber wesentlich geringer ist als die Aufspaltung der Energieterme durch das Magnetfeld. In Klammern sind die Quantenzahlen (m_l, m_s) angegegeben. b) Die beiden s-Linien des Lorentz-Tripletts spalten durch die Feinstrukturwechselwirkung in zwei Linien auf.

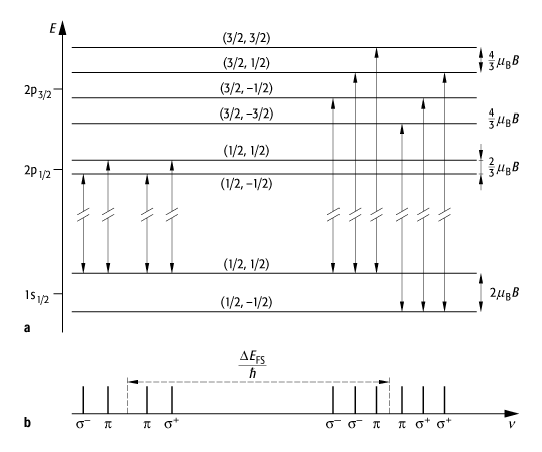
Zeeman-Effekt 3: Anomaler Zeeman-Effekt des Wasserstoffatoms. a) Die Feinstruktur-Energieniveaus erfahren eine zusätzliche Aufspaltung durch das äussere, schwache Magnetfeld. In diesem Fall ist die Aufspaltung durch das Magnetfeld viel kleiner als die Feinstrukturaufspaltung DE(2p_3/2 – 2p_1/2). In Klammern sind die Quantenzahlen (J, m_J) angegeben. b) Die beiden Feinstrukturspektrallinien sind in einem wesentlich komplizierteren Muster aufgespalten als beim normalen Zeeman-Effekt.

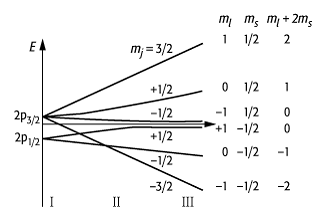
Zeeman-Effekt 4: Aufspaltung der Energieniveaus des n = 2, l = 1 Zustandes des Wasserstoffatoms im Magnetfeld als Funktion der magnetischen Feldstärke B. Im schwachen Magnetfeld sind die Niveauabstände unsymmetrisch (Bereich I, anomaler Zeeman-Effekt), im starken Magnetfeld sind sie symmetrisch zum unverschobenen Zustand aufgespalten (Bereich III, Paschen-Back-Effekt). Der intermediäre Bereich II ist schwierig zu analysieren.