Techniklexikon

Noether-Theorem

Teilchenphysik, in der Feldtheorie der von Emmy Noether bewiesene mathematische Satz, dass die Invarianz (bis auf eine Divergenz) des n-dimensionalen Wirkungsintegrals  gegenüber einer r-parametrigen stetigen Transformationsgruppe G_r (Lie-Gruppe) die Existenz von r lokalen Erhaltungssätzen zur Folge hat. Das Noether-Theorem ist für die Physik von überaus grosser Bedeutung, da es die Symmetrieeigenschaften eines physikalischen Systems, ausgedrückt durch G_r, mit den Erhaltungssätzen in Beziehung setzt. Es sei  ein beliebiger Punkt des Raum-Zeit-Kontinuums und  die Lagrange-Dichte. Dann folgt insbesondere aus der Invarianz gegenüber den vier Translationen  die Existenz des kanonischen Energie-Impuls-Tensors

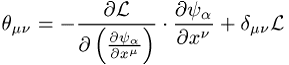
mit dem Kronecker-Symbol , dessen Divergenz verschwindet:

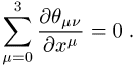
 ist dabei die Energiedichte des Feldes. Aus dem Noether-Theorem folgt so die Erhaltung von Energie und Impuls des als abgeschlossenes System aufgefassten Feldes . Analog folgen die Erhaltung des Drehimpulses und der Schwerpunktsatz aus der Drehinvarianz, die im vierdimensionalen Raum-Zeit-Kontinuum die gewöhnlichen Lorentz-Transformationen einschliesst. Aus der Invarianz gegenüber Eichtransformationen, die nur die Felder abändern, folgt die Ladungserhaltung.