Techniklexikon

Lorentz-Transformation

Relativitätstheorie und Gravitation, affine Transformation, die den Abstand zweier Weltpunkte (Ereignisse)

invariant lässt und daher Inertialsysteme in Inertialsysteme überführt. Sie kann in der Form

parametrisiert werden, wobei die Matrix  aufgrund der Invarianzforderung die Bedingung

erfüllen muss. Der Abstand zweier Ereignisse kann dabei positiv, negativ oder null sein. Die Flächen  sind Hyperboloide im Raum- und Zeitkontinuum, die sich an den durch  definierten Lichtkegel anschmiegen. Die Raumzeit zerfällt also in separierte, durch das Vorzeichen des Abstandes zweier Weltpunkte charakterisierte Gebiete: die Region mit  heisst zeitartig, die mit  lichtartig und die mit  raumartig, wobei diese Regionen nicht durch eine Lorentz-Transformation verbunden werden können.

Die spezielle Lorentz-Transformation zwischen zwei Koordinatensystemen, die sich relativ zueinander entlang der räumlichen 1-Achse mit der Geschwindigkeit  bewegen, hat die explizite Gestalt

wobei  und .  lässt sich durch  parametrisieren; die zugehörige Matrix lautet also

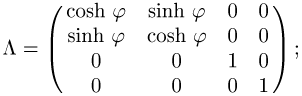
sie erzeugt einen Lorentz-Boost in x-Richtung. Er kann analog zu einer Drehung im euklidischen Raum auch als Pseudodrehung, bei der die Funktionen des Drehwinkels Hyperbelfunktionen sind, aufgefasst werden (siehe Abb.).

Entsprechend konstruiert man Lorentz-Boosts in y- und z-Richtung. Zwei hintereinander ausgeführte Boosts erzeugen aber keinen anderen reinen Boost, sondern zusätzlich eine räumliche Drehung; die allgemeinen Lorentz-Transformationen setzen sich also aus Boosts und Drehungen zusammen und bilden die Lorentz-Gruppe.

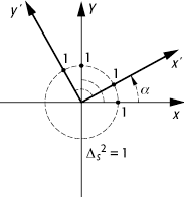
Lorentz-Transformation: Oben: Übergang von einem in ein anderes Koordinatensystem in der euklidischen Ebene. Der Winkel a zwischen den Achsen bleibt fest. Die Kurve mit dem Abstand  ist ein Kreis mit Radius 1.

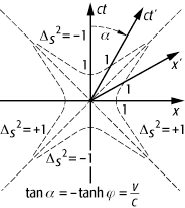
Unten: Eine spezielle Lorentz-Transformation (Boost) als Pseudodrehung. Die Winkelhalbierende (Lichtkegel) zwischen den Achsen bleibt fest. Die Kurven mit  sind Hyperbeln.