Solitonen

QuantenmechanikOptik, stabile Lösungen von eindimensionalen, nichtlinearen Wellengleichungen mit teilchenartigem Charakter. Die erste Lösung dieser Art wurde für die Korteweg-de-Vries-Gleichung gefunden. Heute sind für viele Differentialgleichungen Soliton-Lösungen bekannt, unter anderem für die nichtlineare Schrödinger-Gleichung und die Sinus-Gordon-Gleichung. An Mehr-Soliton-Lösungen kann Streuung von Solitonen beobachtet werden, wobei während der Wechselwirkung teilweise eine komplizierte Verformung auftritt, anschliessend die Lösungen aber wieder ihre ursprüngliche Form annehmen. Diesem teilchenartigen Verhalten verdanken die Solitonen ihren Namen. Soliton-Lösungen mit Stufenform, beispielsweise zur Sinus-Gordon-Gleichung (siehe Abb.), bezeichnet man auch oft als Kink-Lösungen.

Solitonen treten in zahlreichen naturwissenschaftlichen Gebieten, bei denen nichtlineare Wellenausbreitung vorkommt, auf, z.B. bei Wasserwellen (Tsunamis), bei elektronischen Leitungen, bei der Nervenleitung usw. Eine besondere Bedeutung haben optische Solitonen, vor allem im Hinblick auf ihre technische Anwendung in Lasern und zur Datenübertragung in Glasfasern, da sie auch bei der Übertragung über weite Strecken ihre Form und damit ihre Informationen behalten und nicht wie übliche optische Wellen auf Grund unterschiedlicher Phasengeschwindigkeiten der Wellenkomponenten auseinanderlaufen (Dispersion). Die Effekte der Dispersion werden also gerade durch nichtlineare optische Effekte, v.a. den Kerr-Effekt (Selbstphasenmodulation), kompensiert.

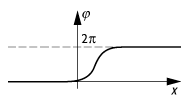
Solitonen: Zeitunabhängige Soliton- bzw. Kink-Lösung zur Sinus-Gordon-Gleichung.