Bethe-Weizsäcker-Formel

Manfred Schönborn
eine 1935 unter Verwendung des Tröpfchenmodells von Weizsäcker hergeleitete und später von Bethe und Fermi verfeinerte Formel zur Berechnung der Bindungsenergie des Atomkerns. Aus der Analogie zwischen dem Verhalten von Kernmaterie und dem einer Flüssigkeit verschafft das Tröpfchenmodell eine Einsicht in den räumlichen Verlauf der Bindungsenergien und damit der Kernmassen. Betrachtet man den Kern als einen Tropfen einer inkompressiblen Flüssigkeit, die durch kurzreichweitige Kräfte mit Sättigungscharakter zusammengehalten wird, ergibt sich die Bindungsenergie B des Tropfens aus folgenden fünf Beiträgen:
1) Hauptbeitrag zur Bindungsenergie ist die Kondensations- oder Volumenenergie, die frei wird, wenn sich die Nukleonen zum Kern vereinen. Dieser Anteil ist durch B1 = aVA gegeben, wobei A die zum Kernvolumen proportionale Anzahl der Nukleonen beschreibt und aV eine Konstante ist.
2) Da die Nukleonen an der Oberfläche des Tropfens weniger stark gebunden sind, wird die Bindungsenergie durch die Oberflächenenergie B2 = - aSA2/3 verringert.
3) Auch wird die Bindungsenergie durch die abstossende Coulomb-Energie der Protonen vermindert, was durch den Term B3 = aCZ2A-1/3 beschrieben wird, wobei Z die Anzahl der Protonen ist.
4) Weiterhin führt der mit steigendem A zunehmende Neutronenüberschuss zu einer Verringerung der Bindungsenergie gegenüber symmetrischen Kernen, was durch die Asymmetrieenergie B4 = - aA(Z - A/2)2/A zum Ausdruck kommt.
5) Aufgrund der Tatsache, dass gepaarte Nukleonen derselben Sorte stets eine besonders hohe Bindungsenergie haben, wird eine mit dem Flüssigkeitsmodell nicht zu erklärende Paarungsenergie hinzugefügt. Sie wird näherungsweise durch die empirische Formel d » aPA-1/2 beschrieben, wobei B5 = + d für gg-Kerne, = 0 für ug- und gu-Kerne und = - d für uu-Kerne ist.
aV, aS, aC, aA und aP sind empirische Konstanten, die sich durch Anpassung an die experimentell ermittelten Werte der Bindungsenergien über einen weiten Massenbereich zu aV = 15,85 MeV/c2, aS = 18,34 MeV/c2, aC = 0,71 MeV/c2, aA = 92,86 MeV/c2 und aP = 11,46 MeV/c2 ergeben.
Damit ergibt sich die Bindungsenergie B aus der Summe der Einzelbeiträge B = B1 + B2 + B3 + B4 + B5, und die Bethe-Weizsäcker-Formel erlaubt unter Verwendung von B die Berechnung der Atommassen m(Z,A) gemäss m(Z,A) = ZmH + (A - Z)mn - aVA + aSA2/3 + aCZ2A - 1/3 + aA(Z - A/2)A - 1 ± d.
Die Massenformel kann nur das mittlere Verhalten der Kerne wiedergeben, nicht jedoch Schalenstruktureffekte. Sie ist daher erst ab etwa A = 30 anwendbar. Es ist in Anbetracht der Einfachheit des Modells bemerkenswert, dass die Bindungsenergien oberhalb von A = 40 mit einer Genauigkeit von 1 % wiedergegeben werden, dies sowohl für stabile als auch für instabile Kerne. Die Massenformel ist im Laufe der Zeit durch Zusatzannahmen verfeinert worden.
Aus der Bethe-Weizsäckerschen Massenformel lassen sich eine Reihe wesentlicher Gesetzmässigkeiten, insbesondere solche bezüglich der Stabilität der Kerne, ableiten; mit ihrer Hilfe kann abgeschätzt werden, unter welchen Umständen die Emission von Teilchen Energie freisetzt, dies besonders im Hinblick auf den a- und den b-Zerfall sowie die Spaltung im allgemeinen. [HG1]
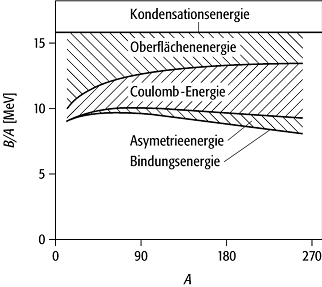
Bethe-Weizsäcker-Formel: Beitrag der einzelnen Terme der Massenformel zur mittleren Bindungsenergie pro Nukleon.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.