Techniklexikon

Bloch-Funktionen

von F. Bloch eingeführte Eigenfunktionen der Schrödinger-Gleichung für ein Elektron in einem gitterperiodischen Potential eines kristallinen Festkörpers (Kristall). Die Bloch-Funktionen beschreiben Elektronenwellen und haben nach dem Bloch-Theorem die Form . Sie beschreiben eine ebene Welle, der eine gitterperiodische Funktion u_k überlagert ist, d.h. es gilt u_k(r) = u_k(r + R) für jeden Gittervektor R. Reicht der Wellenvektor k über die erste Brillouin-Zone hinaus, so kann mit Hilfe eines Vektors G des reziproken Gitters der Wellenvektor auf die erste Zone reduziert werden. Mit k ¢  = k + G erhält man: , wobei y_k¢ wieder eine Bloch-Funktion ist. Mit dem Wellenvektor k ¢ , der innerhalb der ersten Brillouin-Zone liegt, wird der sog. Bloch-Zustand des Elektrons eindeutig beschrieben.

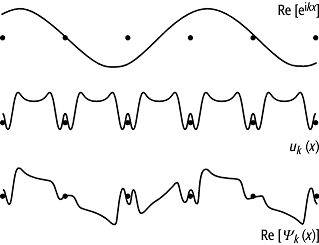
Bloch-Funktionen: Konstruktion einer Bloch-Funktion für ein eindimensionales Gitter aus einer ebenen Welle e^ikx, die mit einer gitterperiodischen Funktion u_k(x) moduliert ist.