Techniklexikon

Koordinatensysteme

Mathematische Methoden und ComputereinsatzAstronomie und Astrophysik, 1) Allgemein: Bezugsrahmen für die Spezifizierung der Lage von Punkten in einem topologischen Raum M. Diese Lage kann durch ein n-Tupel von Zahlen, den Koordinaten, eindeutig spezifiziert werden. Abstrakt kann ein Koordinatensystem über den Körper K eines topologischen Raumes M definiert werden als injektive Abbildung  von einer offenen Teilmenge  in einen Vektorraum über den Körper K endlicher Dimension. Die Koordinaten eines Punktes  sind die Komponenten des Bildpunktes . Für die meisten Anwendungen in Mathematik, Physik und Technik ist K = , M gleich dem gewöhnlichen Ortsraum  oder allgemeiner  und oft wird ein kartesisches Koordinatensystem verwendet. Sinnvollerweise passt man die Wahl des Koordinatensystems den geometrischen Eigenschaften des Raumes an oder konstruiert für Sphären, Tori oder Ellipsoide entsprechende Koordinatensysteme und Koordinaten, z.B. kartesische, schiefwinkelige, konfokale, Polar-, Zylinder-, Torus- oder Ellipsoidkoordinaten. Geben die Koordinaten eines Punktes die Distanz eines Punktes entlang sich senkrecht schneidender Koordinatenachsen an, so spricht man von orthogonalen Koordinaten; die kartesischen Koordinaten und auch die Kugelkoordinaten sind ein Spezialfall orthogonaler Koordinaten. In orthogonalen Koordinaten nehmen die Metrik und Christoffelsymbole (Christoffel-Konnexion) sowie die Differentialoperatoren grad (Gradient), div (Divergenz), rot (Rotation) und der Laplace-Operator einfache Gestalt an; bei schiefwinkeligen Koordinaten treten dagegen Mischterme auf. Ein Koordinatensystem und die Gestalt der Differentialoperatoren in diesem Koordinatensystem ist durch seinen kovarianten Metriktensor  und durch die Massstabs- oder Skalenfaktoren  beschrieben. Damit kann z.B. das Bogenlängenelement oder Linienelement ds und der Abstand zweier Raumpunkte,  und , die durch die Raumkurve ,  verbunden sind, berechnet werden:

 

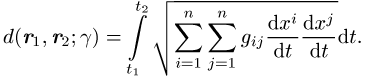
In orthogonalen Koordinatensystemen ist , wobei  das Kronecker-Symbol bezeichnet. Der Übergang oder Wechsel von Koordinatensystemen wird durch eine Koordinatentransformation beschrieben.

2) Astronomie: Einteilung der Himmelssphäre, um die Örter der Gestirne festlegen zu können. In der Astronomie haben sich im wesentlichen vier Koordinatensysteme durchgesetzt, die je nach Anwendungsgebiet verwendet werden.

Die Grundebene des Horizont- oder Azimutsystems wird durch den Horizont definiert. Als Koordinaten verwendet man die Höhe h über dem Horizont und den Winkelabstand a vom Südpunkt in westlicher Richtung entlang des Horizonts. In einigen Fällen wird statt der Höhe auch der Zenitabstand 90° - h verwandt. Da sich die Himmelssphäre infolge der Erdrotation dreht und sich die Sichtbarkeit der Sternbilder im Laufe eines Jahres verändert, sind die Koordinaten eines Gestirns im Horizontsystem abhängig von der Beobachtungszeit. Ausserdem sind sie vom Beobachtungsort abhängig.

Die Grundebene des Äquatorialsystems bildet der Erdäquator, der die Himmelssphäre im Himmelsäquator schneidet. Im festen Äquatorialsystem, auch Stundenwinkelsystem, nennt man alle Grosskreise, die senkrecht auf der Äquatorebene stehen, Stundenkreise. Den Nullpunkt dieses Systems bildet der Schnittpunkt des Meridians mit dem Himmelsäquator. Als Stundenwinkel t eines Gestirns bezeichnet man dann den Abstand zwischen dem Schnittpunkt seines Stundenkreises mit der Äquatorebene und dem Nullpunkt. Die zweite Koordinate, die Deklination d, ist der Winkelabstand zur Äquatorebene. Die Deklination eines Gestirns ist fest, während sich der Stundenwinkel mit der täglichen Scheindrehung der Himmelssphäre verändert. Der Stundenwinkel wird in Stunden, Minuten und Sekunden angegeben. Für die Positionsbestimmung eines Gestirns ist die Angabe des Beobachtunsgzeitpunktes und des Ortes notwendig. Im beweglichen Äquatorsystem oder Rektaszensionssystem wird der Frühlingspunkt  als Leitpunkt gewählt. Der Winkel zwischen ihm und dem Schnittpunkt des Himmelsäquators mit dem Stundenkreis des Gestirns wird als Rektaszension a bezeichnet. Die Deklination ist hier wieder die zweite Koordinate. Das bewegliche Äquatorsystem entspricht einer Projektion des Längen- und Breitengradsystems auf der Erde an die Himmelssphäre. Dieses System nimmt daher an der täglichen Scheindrehung der Himmelssphäre teil. Die Koordinaten eines Gestirns sind unabhängig von der Beobachtungszeit und dem Ort. Es ist das gängige Koordinatensystem für Sternkataloge.

Die Grundebene des Ekliptiksystems bildet die Ekliptik. Alle auf ihr senkrecht stehenden Grosskreise nennt man ekliptikale Länge, wobei der Frühlingspunkt den Nullpunkt bildet. Die ekliptikale Breite ist der Winkelabstand von der Ekliptik entlang eines Längenkreises. Das Ekliptiksystem nutzt man zur Positionsbestimmung von Körpern im Sonnensystem.

Grundebene des Galaktischen Systems ist die Ebene des Milchstrassensystems, der Nullpunkt des galaktischen Äquators ist das galaktische Zentrum. Die galaktische Länge wird von hier aus in Grad gezählt, die galaktische Breite ist der Winkelabstand vom galaktischen Äquator entlang eines Längenkreises. Dieses Koordinatensystem wird insbesondere im Zusammenhang mit der Erforschung der räumlichen Struktur des Milchstrassensystems verwendet. Positionen der Gestirne sind hierin unabhängig vom Beobachtungszeitpunkt und dem Ort.

Äquator- und Ekliptiksystem unterliegen über längere Zeiträume hinweg Schwankungen aufgrund von Präzession und Nutation der Erdrotationsachse. Die Positionsangabe eines Gestirns muss sich daher stets auf ein bestimmtes Datum, eine Epoche, beziehen.

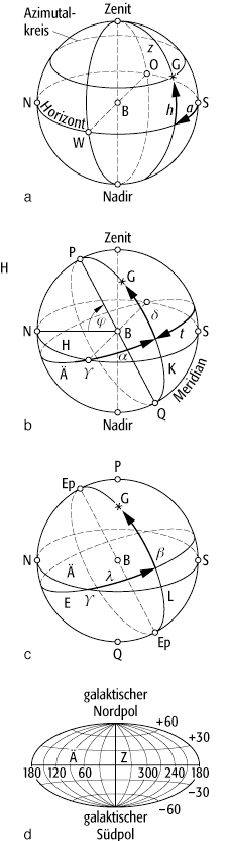
Koordinatensysteme: Die vier wesentlichen astronomischen Koordinatensysteme (B: Beobachtungspunkt, N: Norden, S: Süden, P: nördlicher Himmelspol, Q: südlicher Himmelspol, G: Gestirn): a) Horizontsystem (z: Zenitdistanz, h: Höhe, a: Azimut, W: Westen, O: Osten), b) Äquatorsystem (j: geographische Breite,¡: Frühlingspunkt, a: Rektaszension, d: Deklination, t: Stundenwinkel, Ä: Himmelsäquator, H: Horizont, K: Stundenkreis), c) Ekliptiksystem (E: Ekliptik, L: Längenkreis, l: ekliptische Länge, b: ekliptische Breite, Ä: Himmelsäquator Ep: Pole der Ekliptik, : Frühlingspunkt),und d) Galaktisches System (Ä: galaktischer Äquator, Z: galaktisches Zentrum).