Techniklexikon

nicht-konservative Kraft

Klassische Mechanik, eine Kraft, die sich nicht aus einem Potential ableiten lässt. Beispiele sind geschwindigkeitsabhängige Kräfte, wie z.B. die Reibungskraft in der Mechanik oder die Lorentz-Kraft in der Elektrodynamik. Im Rahmen der analytischen Mechanik kann ein generalisiertes Potential  in die Lagrange-Funktion eingeführt werden. Im Falle der Bewegung einer Ladung q mit der Geschwindigkeit v im elektrostatischen Potential f und im vom Magnetfeld herrührenden Vektorpotential A lautet das generalisierte Potential . Aus ihm kann die Lorentz-Kraft gemäss

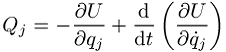
abgeleitet werden. Falls ein generalisiertes Potential nicht gefunden werden kann, lassen sich die Lagrangeschen Gleichungen immer schreiben als

.

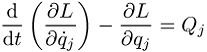Die konservativen Kräfte sind in Form des Potentials V in  enthalten, die nicht-konservativen Kräfte tauchen als Q_j in den Gleichungen auf.