Techniklexikon

Schalenmodell

Kernphysik, Beschreibung der Nukleonenbewegung im Kern, die der Behandlung der Elektronenbewegung in der Elektronenhülle eines Atoms (Atomhülle) entspricht. Unter einer Schale versteht man dabei mehrere nebeneinander liegende Energiezustände, die deutlich getrennt von anderen Zuständen liegen. Das Schalenmodell dient als Grundlage zur Beschreibung spezieller Erscheinungen angeregter Kerne. Ein deutlicher Hinweis auf die Existenz schalenähnlicher Strukturen ist dabei das Auftreten besonders stabiler Kernkonfigurationen; Kerne, deren Protonenzahl Z oder Neutronenzahl N eine der magischen Nukleonenzahlen  oder 126 beträgt, besitzen eine besonders hohe Bindungsenergie. Analog zu den Elektronenschalen von Edelgasatomen (Edelgase) wird als Erklärung angenommen, dass bei diesen Kernen die Protonen- bzw. Neutronenschalen vollständig gefüllt und somit abgeschlossen sind.

In der einfachsten Ausführung wird der Kern näherungsweise als ein System voneinander unabhängiger Nukleonen in einem mittleren sphärischen Potential betrachtet, wobei sich die Drehimpulse von Proton und Neutron getrennt paarweise aufheben, so dass nur das letzte ungerade Nukleon zu den Eigenschaften der Kernniveaus beiträgt. Weiterführende Modelle berücksichtigen die Restwechselwirkung zwischen den Nukleonen, die Deformation des Kernpotentials (Kerndeformation) sowie die Drehimpulskopplung von Nukleonen ausserhalb abgeschlossener Schalen.

Ein wesentlicher Unterschied im Vergleich zur Beschreibung der Elektronenhülle ist, dass im ausgedehnten Kern kein gemeinsames Kraftzentrum existiert. Ausserdem ist der Einfluss der Spin-Bahn-Kopplung wesentlich ausgeprägter und spielt beim Verständnis der magischen Zahlen eine entscheidende Rolle. Während die Spin-Bahn-Kopplung im Atom die Feinstrukturaufspaltung (Feinstruktur) mit einer kleinen Korrektur (Feinstrukturkonstante) verursacht, bewirkt der Spin-Bahn-Term des Kernpotentials eine grosse Energieaufspaltung der Zustände und damit die Schalenstruktur.

In der Abb. ist die Niveaufolge des Schalenmodells unter Berücksichtigung der Spin-Bahn-Aufspaltung dargestellt. Dabei kann jedes Niveau zu gegebenem Gesamtdrehimpuls j mit 2j + 1 Nukleonen besetzt werden. Ein Schalenabschluss liegt dann vor, wenn der Abstand zum nächsten Energieniveau besonders gross ist.

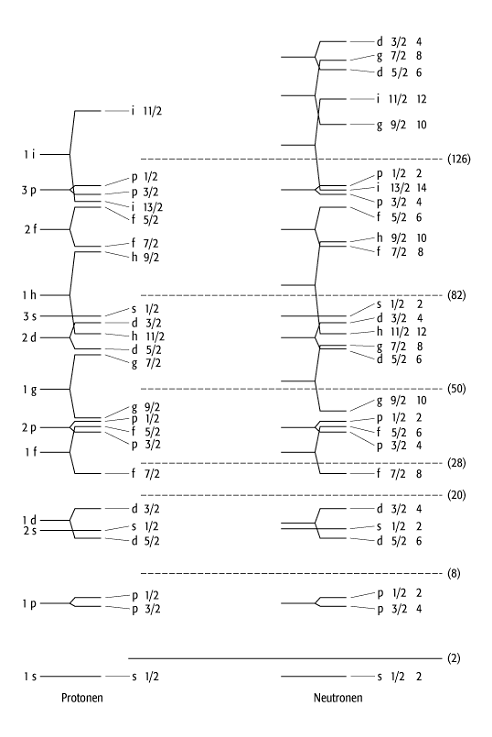
Schalenmodell: Energieniveaus des Schalenmodells unter Berücksichtigung der Spin-Bahn-Aufspaltung. Jedes Niveau mit Gesamtdrehimpuls j kann mit 2j + 1 Nukleonen besetzt werden. Rechts sind diese Besetzungszahlen aufgelistet: Für den Zustand 1p3 / 2 ist z.B. j = 3 / 2 und die mögliche Besetzungszahl 2 (3 / 2) + 1 = 4. Summiert man die Besetzungszahlen kumulativ auf, so sieht man, dass bei den magischen Zahlen  (Zahlen in runden Klammern) in der Tat besonders grosse Energieabstände auftreten; es liegt dann ein Schalenabschluss vor.