Stabilität der Materie

Irene Kramer-Schwenk
Physik
im Alltag, die Tatsache, dass sowohl Einzelatome (mikroskopische Stabilität) als
auch Atomaggregate im Limes grosser Teilchenzahl ![]() (makroskopische Stabilität) gegen die
Coulomb-Anziehung (Coulomb-Gesetz) stabil sind; beides braucht zur Erklärung
ganz entscheidend die Quantenphysik.
(makroskopische Stabilität) gegen die
Coulomb-Anziehung (Coulomb-Gesetz) stabil sind; beides braucht zur Erklärung
ganz entscheidend die Quantenphysik.
Die mikroskopische Stabilität stellt insofern ein Problem dar,
da in der klassischen Physik die Elektronen nichts am »Sturz in den
Coulomb-Trichter« des Kernes hindert. Die Lösung des Problems beruht auf der
quantenmechanischen Lokalisierungsenergie, d.h. auf der Tatsache, dass wegen ![]() die kinetische Energie nach unten beschränkt
ist,
die kinetische Energie nach unten beschränkt
ist,
![]()
und Dp2 seinerseits bei zunehmender Lokalisierung des Teilchens so
stark anwächst, dass die Potentialenergie ![]() kompensiert werden kann; gilt aber für jeden
Zustand
kompensiert werden kann; gilt aber für jeden
Zustand
![]()
so gilt es auch für den Grundzustand.
Die übliche Abschätzung ![]() auf der Basis der Heisenbergschen
Unschärferelation genügt jedoch nicht für die gewünschte Ungleichung (2). Denn
auf der Basis der Heisenbergschen
Unschärferelation genügt jedoch nicht für die gewünschte Ungleichung (2). Denn ![]() kann endlich sein, auch wenn es
kann endlich sein, auch wenn es ![]() nicht ist; in diesem Fall kann ELok
nicht U kompensieren und
nicht ist; in diesem Fall kann ELok
nicht U kompensieren und ![]() divergiert trotz der Unschärferelation.
divergiert trotz der Unschärferelation.
Man braucht eine stärkere Abschätzung, die geliefert wird durch
![]()
(von R. Peierls), also ![]() . Dann hat
. Dann hat ![]() ein Minimum, weil die zu mittelnde Funktion
eines hat (siehe Abb.1).
ein Minimum, weil die zu mittelnde Funktion
eines hat (siehe Abb.1).
Die makroskopische Stabilität stellt nun auch ein Problem dar,
denn wendet man obiges Lokalisierungsargument bei N
Atomen an, so wäre bei unveränderter Ladungsverteilung um ein Einzelatom für
jedes Elektron eine Umverteilung auf das N-fache
Volumen möglich (siehe Abb.2); da so eine verkleinerte Lokalisierungsenergie ELok
einer unveränderten elektrostatischen Anziehung ![]() widerstehen muss, erwartet man, dass EMin
mit zunehmendem N immer negativer und das
Atomvolumen V immer kleiner wird. Dies zeigt die
Rechnung in der Tat, und weiterhin, dass die gesamte Bindungsenergie -N × EMin
stärker als linear in N steigt, das Gesamtvolumen N × V aber sogar
abnimmt, d.h. eine nur durch die Lokalisierungsenergie stabilisierte Materie
würde mit
widerstehen muss, erwartet man, dass EMin
mit zunehmendem N immer negativer und das
Atomvolumen V immer kleiner wird. Dies zeigt die
Rechnung in der Tat, und weiterhin, dass die gesamte Bindungsenergie -N × EMin
stärker als linear in N steigt, das Gesamtvolumen N × V aber sogar
abnimmt, d.h. eine nur durch die Lokalisierungsenergie stabilisierte Materie
würde mit ![]() unter Aussendung immer grösserer Energiemengen
implodieren.
unter Aussendung immer grösserer Energiemengen
implodieren.
Die Lösung des Problems liegt im Pauli-Prinzip: N Elektronen können nicht in identischer Weise verteilt werden, sondern ihre Zustandsfunktion ist zu antisymmetrisieren. Dass dann in der Tat Gesamtenergie und -volumen proportional zu N, d.h. extensive Grössen sind, kann mit der Thomas-Fermi-Theorie streng gezeigt werden.
Versteht man das Pauli-Prinzip als etwas wesensmässig Quantenphysikalisches, so gilt: Die höchst alltägliche Tatsache der Stabilität der Materie ist ein makroskopischer Quanteneffekt.
Die Stabilisierung der Materie gegen die Coulomb-Anziehung durch das Pauli-Prinzip ist eher eine Ausnahme; für stärker divergierende oder rein anziehende Kraftgesetze sowie für Bosonen ergibt sich immer Instabilität (siehe Tab.). Die Gravitationsinstabilität insbesondere wird durch das Jeans-Kriterium beschrieben.
Stabilität der Materie: Die Stabilität der Materie gegen Gravitations- und Coulomb-Anziehung. Nur für Fermionen unter Coulomb-Anziehung ergeben sich Gesamtvolumen und -energie (N × V; N × EMin) proportional zur Teilchenzahl.
| bottom-alt:solid black .6pt;padding:0cm 3.55pt 0cm 3.55pt\'>
|
bottom:solid black 1.0pt;border-right:none;
mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt;
padding:0cm 3.55pt 0cm 3.55pt\'>
N × V |
bottom-alt:
solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
N × EMin |
|
Coulomb / Bosonen |
~ N-1 |
~ -N5 / 3 |
|
Coulomb / Fermionen |
~ N |
~ -N |
|
Gravitation / Bosonen |
~ N-3 |
~ -N-3 |
| bottom:solid black 1.0pt;border-right:none;
mso-border-left-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt;
padding:0cm 3.55pt 0cm 3.55pt\'>
Gravitation / Fermionen |
bottom:solid black 1.0pt;border-right:none;mso-border-left-alt:solid black .75pt;
mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
~ N-1 |
bottom-alt:
solid black .75pt;mso-border-right-alt:solid black .6pt;padding:0cm 3.55pt 0cm 3.55pt\'>
~ -N7 / 3 |
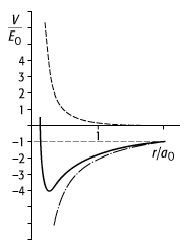
Stabilität der Materie 1: Das effektive Gesamtpotential
(mittlere Kurve) als Summe von Coulomb-Potential (untere Kurve,
strich-punktiert) und Lokalisierungsenergie (obere Kurve, gestrichelt). Das
Minimum von ![]() liegt bei
liegt bei ![]() und
und ![]() (E0, a0: Bohr-Energie und -Radius).
(E0, a0: Bohr-Energie und -Radius).
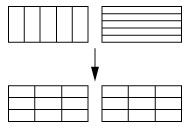
Stabilität der Materie 2: »Delokalisierungs-Umverteilung«: Die beiden »Teilchen« (senkrechte und waagrechte Striche) sind unten bei gleicher »Ladungsdichte« (gesamte Strichzahl) jeweils auf die doppelte Fläche verteilt.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.