Tensoralgebra

Julian Schultheiss
Mathematische Methoden und Computereinsatz, Formalismus, der beschreibt, welche algebraischen Operationen beim Umgang mit Tensoren in welcher Weise möglich sind. Hierzu gehören die Summation von Tensoren (sie erfolgt komponentenweise und ist kommutativ), die Multiplikation mit Skalaren, Vektoren und Tensoren, die Verjüngung und Überschiebung von Tensoren sowie das Transformationsverhalten von Tensoren. Diese folgen den Regeln der linearen Algebra; aus historischen Gründen liegt der Tensoralgebra noch ein eigentümlicher Formalismus zugrunde, der hier kurz beleuchtet werden soll.
Zunächst seien Tensoren 1. Stufe, d.h. Vektoren, betrachtet.
Sei in einem ![]() -dimensionalen
euklidischen Vektorraum eine Basis
-dimensionalen
euklidischen Vektorraum eine Basis ![]() mit
mit ![]() Basisvektoren
Basisvektoren ![]() gegeben. Ein beliebiger Vektor
gegeben. Ein beliebiger Vektor ![]() besitzt dann gemäss der Eigenschaften eines
Vektorraums die Darstellung
besitzt dann gemäss der Eigenschaften eines
Vektorraums die Darstellung ![]() , wobei
nach den Regeln der Tensoralgebra die Einsteinsche Summenkonvention verwendet
wird. Der Betrag des Vektors ergibt sich zu
, wobei
nach den Regeln der Tensoralgebra die Einsteinsche Summenkonvention verwendet
wird. Der Betrag des Vektors ergibt sich zu ![]() , wobei
die Metrikkoeffizienten
, wobei
die Metrikkoeffizienten ![]() später als Metriktensor
später als Metriktensor ![]() bezeichnet werden. Neben der bisher
betrachteten Basis
bezeichnet werden. Neben der bisher
betrachteten Basis ![]() , die in
der Tensoralgebra auch kovariante Basis genannt wird, wird vermöge der
Skalarprodukt-Beziehung
, die in
der Tensoralgebra auch kovariante Basis genannt wird, wird vermöge der
Skalarprodukt-Beziehung ![]() mit Kroneckersymbol
mit Kroneckersymbol ![]() die kontravariante Basis
die kontravariante Basis ![]() eingeführt. Schreibt man die Basisvektoren
eingeführt. Schreibt man die Basisvektoren ![]() als Spalten einer Matrix
als Spalten einer Matrix ![]() , so ist
die Matrix
, so ist
die Matrix ![]() der kontravarianten Basis also durch die
Bedingung
der kontravarianten Basis also durch die
Bedingung ![]() gegeben, also
gegeben, also ![]() bzw.
bzw. ![]() und
und ![]() , wobei
sich die Matrix
, wobei
sich die Matrix ![]() der kontravarianten Metrikkoeffizienten
ebenfalls als inverse Matrix von
der kontravarianten Metrikkoeffizienten
ebenfalls als inverse Matrix von ![]() ergibt. Der oben betrachtete Vektor
ergibt. Der oben betrachtete Vektor ![]() lässt sich nun sowohl bezüglich der kovarianten
als auch der kontravarianten Basis darstellen:
lässt sich nun sowohl bezüglich der kovarianten
als auch der kontravarianten Basis darstellen: ![]() , wobei
die
, wobei
die ![]() die kovarianten und die
die kovarianten und die ![]() die kontravarianten Komponenten des Vektors
die kontravarianten Komponenten des Vektors ![]() genannt werden. Zu den Basisoperationen der
Tensoralgebra gehören das Heraufziehen des Index (Beispiel:
genannt werden. Zu den Basisoperationen der
Tensoralgebra gehören das Heraufziehen des Index (Beispiel: ![]() ) und
Herunterziehen des Index (Beispiel:
) und
Herunterziehen des Index (Beispiel: ![]() ). Geht
man nun mit Hilfe einer linearen Transformation
). Geht
man nun mit Hilfe einer linearen Transformation ![]() von einer bestimmten kovarianten Basis
von einer bestimmten kovarianten Basis ![]() zu einer anderen kovarianten Basis
zu einer anderen kovarianten Basis ![]() (bzw.:
(bzw.: ![]() ) über, so
wird der umgekehrte Übergang von
) über, so
wird der umgekehrte Übergang von ![]() nach
nach ![]() gerade durch die inverse Transformationsmatrix
gerade durch die inverse Transformationsmatrix
![]() vollzogen. Ein Vektor
vollzogen. Ein Vektor ![]() bzw. jeder Tensor 1. Stufe transformiert sich
wie die Basis, d.h.
bzw. jeder Tensor 1. Stufe transformiert sich
wie die Basis, d.h. ![]() ;
derartiges Transformationsverhalten heisst kogredient. Kovariante und
kontravariante Koeffizienten kontrahieren sich dagegen kontragredient
zueinander.
;
derartiges Transformationsverhalten heisst kogredient. Kovariante und
kontravariante Koeffizienten kontrahieren sich dagegen kontragredient
zueinander.
Das einfachste Beispiel eines Tensors 2. Stufe lässt sich aus
dem dyadischen Produkt ![]() zweier Vektoren ableiten, wobei
zweier Vektoren ableiten, wobei ![]() die kontravarianten,
die kontravarianten, ![]() die kovarianten,
die kovarianten, ![]() und
und ![]() die gemischt kovariant-kontravariante
Komponenten genannt werden und
die gemischt kovariant-kontravariante
Komponenten genannt werden und ![]() die kovariante,
die kovariante, ![]() die kontravariante und
die kontravariante und ![]() und
und ![]() gemischte Basen darstellen. Für dyadische
Produkte gelten ferner das Distributivgesetz
gemischte Basen darstellen. Für dyadische
Produkte gelten ferner das Distributivgesetz ![]() und das Assoziativgesetz
und das Assoziativgesetz ![]() . Das
Transformationsverhalten eines Tensors 2. Stufe ist durch
. Das
Transformationsverhalten eines Tensors 2. Stufe ist durch ![]() bzw.
bzw. ![]() charakterisiert, wobei
charakterisiert, wobei ![]() die Koeffizienten der inversen
Transformationsmatrix
die Koeffizienten der inversen
Transformationsmatrix ![]() bezeichnet. Durch Multiplikation mit den
Metrikkoeffizienten können Indizes herunter- und heraufgezogen werden, z.B.
bezeichnet. Durch Multiplikation mit den
Metrikkoeffizienten können Indizes herunter- und heraufgezogen werden, z.B.
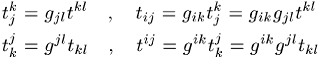
Die »verjüngende« Multiplikation eines Tensors 2. Stufe ![]() mit einem Tensor 1. Stufe
mit einem Tensor 1. Stufe ![]() erzeugt mit der Vorschrift
erzeugt mit der Vorschrift
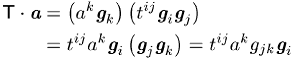
einen neuen Vektor, ebenso wie die verjüngende Multiplikation von links gemäss
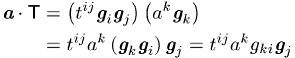
erfolgt.
Ein Tensor ![]() -ter Stufe
lässt sich definieren als Grösse, deren Basis ein tensorielles Produkt von
-ter Stufe
lässt sich definieren als Grösse, deren Basis ein tensorielles Produkt von ![]() Grundvektoren, also
Grundvektoren, also
![]()
ist; entsprechend gibt es ![]() Arten von Komponenten: rein kovariante, rein
kontravariante und
Arten von Komponenten: rein kovariante, rein
kontravariante und ![]() Arten gemischter Komponenten. Die Behandlung
derartiger Tensoren folgt der allgemeinen Transformationsregel, dass für jeden
kovarianten bzw. kontravarianten Index dieselben Transformationsregeln wie für
die kovarianten bzw. kontravarianten Komponenten eines Tensors 1. Stufe gelten.
Arten gemischter Komponenten. Die Behandlung
derartiger Tensoren folgt der allgemeinen Transformationsregel, dass für jeden
kovarianten bzw. kontravarianten Index dieselben Transformationsregeln wie für
die kovarianten bzw. kontravarianten Komponenten eines Tensors 1. Stufe gelten.
Anders als das verjüngende Produkt ergibt das tensorielle
Produkt zweier Tensoren ![]() und
und ![]() einen Tensor
einen Tensor ![]()
![]() -ter
Stufe; es ist assoziativ, jedoch nicht kommutativ. Beispiel:
-ter
Stufe; es ist assoziativ, jedoch nicht kommutativ. Beispiel:
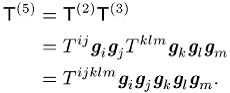
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.