Techniklexikon

CKM-Matrix

(Cabibbo-)Kobayashi-Maskawa-Matrix, unitäre 3 ´ 3-Matrix, die den Übergang zwischen den physikalischen Masse-Eigenzuständen der Quarks und ihren schwachen Eigenzuständen, die durch die SU(2) ´ U(1)-Eichgruppe des elektroschwachen Standardmodells (GWS-Modell) festgelegt werden, beschreibt; sie mischt also die drei Quarkgenerationen untereinander und stellt somit eine Erweiterung des von Cabibbo eingeführten Mischungswinkels für zwei Quarkgenerationen dar (Cabibbo-Winkel). Fasst man die Quarks mit Ladung + 2/3 (u, c und t) und Ladung  - 1/3 (d, s, b) jeweils zu Multipletts zusammen,

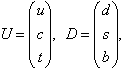
lässt sich die Mischung der Quarkgenerationen in U und D allgemein durch zwei unitäre 3 ´> 3-Matrizen M_U und M_D beschreiben,

U ¢  = M_UU, D ¢  = M_DD.

Der geladene Strom schreibt sich dann in der Form

wobei

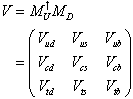
die CKM-Matrix ist. In dieser Schreibweise zeigt sich ihre physikalische Signifikanz, da sich die Matrixelemente V_ij, deren Festlegung ein intensiver Forschungsgegenstand ist, prinzipiell aus den schwachen Zerfällen der relevanten Quarks (z.B. V_ud aus dem Übergang d  u, der dem Betazerfall zugrunde liegt) oder mit Hilfe der tief-inelastischen Neutrino-Streuung bestimmen lassen. Fasst man den aktuellen experimentellen Stand zusammen (Tabelle),

ergibt sich für die Beträge der komplexen Matrixelemente (90%-Konfidenzintervall)

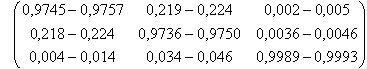
Die Matrixelemente, die das Top-Quark involvieren (V_td, V_ts und V_tb), werden in dieser Aufstellung allein mit Hilfe der Unitarität, die verschiedene Matrixelemente miteinander verknüpft, bestimmt. Die angegebenen Bereiche für die Matrixelemente des Top-Quarks sind aber mit indirekten experimentellen Informationen über das Top-Quark verträglich.

Die CKM-Matrix enthält nur vier unabhängige Parameter, lässt sich also auf verschiedene Weise durch vier unabhängige Grössen parametrisieren. Kobayashi und Maskawa wählten ursprünglich vier Winkel q₁, q₂, q₃ und d in der Darstellung

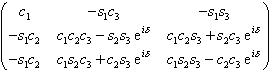
mit den Abkürzungen c_i = cosq_i und s_i = sinq_i ist. In der Folge wurden aber auch zahlreiche andere Parametrisierungen eingeführt. Die Particle Data Group schlägt als "Standard"-Parametrisierung

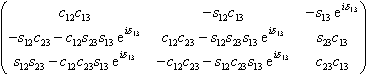
mit der Benutzung "Generationen"-indizierter Winkel q₁₂, q₁₃ und q₂₃ vor. Im Grenzfall q₁₃ = q₂₃ = 0 entkoppelt die dritte Generation, und man erhält für die ersten beiden Generationen die übliche Cabibbo-Mischung mit dem Cabibbo-Winkel q₁₂. Die Phase d₁₃ hat zwar keinen Einfluss auf die Beträge der Matrixelemente, ihr Zahlenwert ist jedoch insofern von grosser Bedeutung, als dass ein Wert ungleich null die CP-Verletzung der schwachen Wechselwirkung erklären würde, da alle möglichen CP-verletzenden Amplituden im Standardmodell (in der obigen "Standard"-Parametrisierung) proportional zur der Parameterkombination  sind. Bisher wurde CP-Verletzung nur im System der neutralen Kaonen beobachtet. Aber die aus diesen Experimenten ableitbaren Einschränkungen insbesondere an die Phase d₁₃ sowie die immer genauere Bestimmung der CKM-Matrixelemente ergeben Hinweise auf zukünftige Messungen von CP-verletzenden Prozessen im System der B-Mesonen. [UK]

CKM-Matrix: Experimentelle Bestimmung der Matrixelemente.

bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> Matrixelement	bottom:solid black 1.0pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'> Prozesse	bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> Werta
	Beta-Zerfall/Myon-Zerfall	0,9736±0,0010
	Kl3-Zerfall/Hyperon-Zerfall	0,2205±0,0018
	n-Produktion	0,224±0,016
		1,01±0,18
	semileptonische B-Zerfälle	0,08±0,02
bottom:solid black 1.0pt;border-right:none; mso-border-left-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'>	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> semileptonische B-Zerfälle	bottom:solid black 1.0pt;border-right:solid black 1.0pt;mso-border-bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 0,041±0,003

^aQuelle: Phys.Rev. D54 (1996), Rev. of Particle Physics)