Techniklexikon

getriebenes Pendel

Nichtlineare Dynamik, Chaos, Fraktale, ein einfaches Beispiel für ein getriebenes System. Die Bewegungsgleichung lautet  und beschreibt die Bewegung eines Pendels (Auslenkung q) im Schwerefeld unter dem Einfluss von Reibung (Dämpfungskonstante g) und einer externen periodischen Kraft (Amplitude A, Frequenz w). Die Bewegung ist i.a. chaotisch (deterministisches Chaos) auf einem Seltsamen Attraktor. Es können auch mehrere einfache Attraktoren koexistieren, wobei sich komplexe Attraktorbassins ausbilden können.

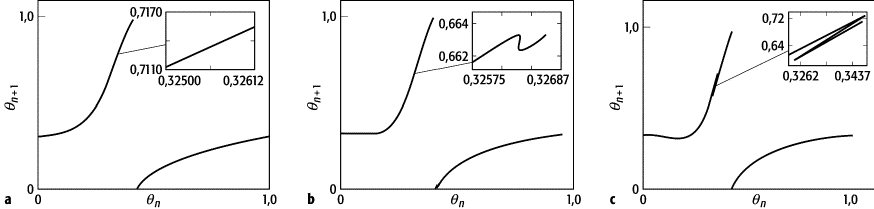
getriebenes Pendel: Poincaré-Schnitt einer numerischen Integration der Pendelgleichung mit A = 0, w = 1,76. a) g = 1,576, W = 2p(A + B) / (wg) = 1,4: lineares Verhalten; b) g = 1,253, W = 1,2: kubischer Wendepunkt (Vergrösserung); c) g = 1,081, W = 1,094: chaotisches Verhalten (Vergrösserung).