Techniklexikon

kinetische Gastheorie

Teilgebiet der Statistik, das sich ausschliesslich auf Gesetzmässigkeiten der klassischen Teilchenmechanik stützt, d.h. alle makroskopischen Aussagen über irreversible Prozesse aus den Wechselwirkungen der Mikroteilchen, aus denen das makroskopische System zusammengesetzt ist, abzuleiten versucht. Es trug damit wesentlich zur Auffassung des 19.Jh. bei, alle physikalischen Erscheinungen seien auf die Mechanik zurückführbar.

Die kinetische Gastheorie geht von dem Ansatz aus, dass sich in Gasen die Moleküle weitgehend unabhängig voneinander als freie Teilchen mit vernachlässigbarem Eigenvolumen (Massenpunkte) bewegen und nur bei starker Annäherung über kurzzeitige, elastische Stösse miteinander wechselwirken. Die freie Flugzeit ist gross gegenüber der Stossdauer, so dass praktisch nur Zweierstösse vorkommen. Auf diese Weise lassen sich molekularkinetisch alle charakteristischen Eigenschaften eines idealen Gases finden, z.B. der Gasdruck oder die Zustandsgleichungen (Boyle-Mariottesches Gesetz, Avogadrosches Gesetz, Daltonsche Gesetze), ebenso wie die mittlere kinetische Energie 3 / 2 kT eines Moleküls.

Die Verteilungsfunktion der Molekülgeschwindigkeiten gehorcht einer Maxwellschen Verteilung: von den Atomen bzw. Molekülen eines idealen Gases der Teilchenzahldichte n besitzt der Bruchteil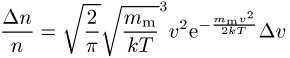

eine Geschwindigkeit zwischen v und v + Dv (m_m: Molekülmasse, k: Boltzmann-Konstante, T: Temperatur).

Ein grundlegender Begriff der kinetischen Gastheorie ist die mittlere freie Weglänge l. Sie ist definiert als der Weg, den Teilchen bei ihrer ungeordneten Wärmebewegung im Mittel zwischen zwei Stössen zurücklegen. Für ein Molekülmodell elastisch stossender starrer Kugeln mit Radius R ergibt sich die mittlere freie Weglänge zu l = (4pR²n)^-1.

In der strengen kinetischen Gastheorie werden die Auswirkungen davon untersucht, dass eine bestimmte Grösse (z.B. die Temperatur) räumlich nicht konstant ist und es daher zu Transportphänomenen, also Nichtgleichgewichtsvorgängen kommt. Eine entsprechende Transportgleichung lässt sich z.B. aus der Boltzmann-Gleichung gewinnen, indem man dieses mit einer beliebigen Transportgrösse multipliziert und über den Geschwindigkeitsraum integriert. Einsetzen expliziter Ausdrücke für die Transportgrösse ergibt dann die makroskopischen Gleichungen (Kontinuitätsgleichung, Bewegungsgleichung etc.). Eine quantentheoretisch strengere kinetische Gleichung als die Boltzmann-Gleichung ist die Uehling-Uhlenbeck-Gleichung, in der u.a. die Nichtunterscheidbarkeit von Teilchen und das Pauli-Prinzip berücksichtigt werden. Eine weitere grundlegende kinetische Gleichung ist die Fokker-Planck-Gleichung.