Techniklexikon

Skalengesetze, biologische

Physik im Alltag, die zwischen vielen biologischen Parametern bestehenden Potenzrelationen vom Typ y ~ bx^a (Gl. 1) (allometrische Gleichung).

Bei a = 1 spricht man von Isometrie. Ein Beispiel für eine zeitliche Isometrie liefert die Tabelle; sie bedeutet z.B., dass das Herz eines Säugers in dessen Leben ca. 1,5 Mrd mal schlägt, unabhängig von der Lebensdauer (man überprüfe für den Menschen mit 1,3 Schlägen / s). Ein wichtiges Beispiel mit a¹1 ist d ~ l^{3 / 2} (Gl. 2) für Abmessungen von Tieren in Längs- (l) und Querrichtung (d) (siehe Abb. 1). Dies folgt aus einer Stabilitätsbedingung: Bei einem bestimmten Verhältnis von Auslenkung (r_F: von der Geometrie des belasteten Körpers abhängiger Formfaktor, F: wirkende Kraft, I_A: Flächenträgheitsmoment, E: Elastizitätsmodul, Biegungspfeil) und Länge l wird die Belastungsgrenze von Knochenmaterial erreicht. Die Knochendimensionen verschiedener Tiere mit gleichem Skelettmaterial sollten also so sein, dass s / l konstant ist; setzt man F ~ M ~ ld² und I_A ~ d⁴ (M: Masse) ein, so folgt Gl. 2. Eine Konsequenz anatomischer Art aus Gl. 2 ist, dass Umfänge U von Gliedmassen und die Masse M sich wie U ~ M^{3 / 8} verhalten, denn U ~ d und M ~ ld² ~ d^{8 / 3} (siehe Abb. 1). Auch der Bauplan vieler Pflanzen spiegelt Gl. 2 wider. Eine Konsequenz physiologischer Art ergibt sich, wenn man erstens annimmt, dass mit dem Skelett auch die anderen anatomischen Strukturen, insbesondere die Muskulatur, Gl. 2 folgen, und zweitens dass die Energiestoffwechselraten proportional zur Kraftentwicklung und damit zum Muskelquerschnitt sind (und nicht zur Masse). Damit folgt R ~ d² ~ M^{3 / 4} (Gl. 3), eines der am besten untersuchten Skalengesetze (Gesetz von Kleiber). Abb. 2 bestätigt dies sehr gut für die Sauerstoffverbrauchsrate, den Nahrungsverbrauch und die Wärmeproduktion. Dennoch ist die Theorie hier nicht vollständig, denn z.B. die Abstrahlung über die Körperoberfläche ist nicht berücksichtigt.

Obige Beispiele zeigen, dass biologische Skalengesetze ein wichtiger Erklärungsfaktor für Formen und Figuren in der belebten Natur sind. Sie zeigen weiter, dass a = 1 geometrische Ähnlichkeit bedeutet, a ¹ 1 hingegen physikalische oder, aus der Sicht der Biologie, funktionale Ähnlichkeit: Die Grössenverhältnisse sind so, dass eine bestimmte physikalische Grösse (z.B. die relative Durchbiegung) für viele Lebewesen (annähernd) gleich ist, und damit die daran geknüpfte biologische Funktion.

Ausser aus einer problemspezifischen Forderung nach physikalischer Ähnlichkeit wie bei Gl. 2 lassen sich Skalengesetze auch systematischer aus der Dimensionsanalyse ableiten. Aus der Reynolds-Zahl Re z.B. folgt, dass (Relativ-) Geschwindigkeit v und Länge l verschiedener umströmter Körper sich wie v ~ l^-1 verhalten müssen, damit die sie umgebenden Strömungen den gleichen Turbulenzgrad haben, was z.B. für Wasserlebewesen gerade nicht der Fall ist: Die Welt der kleinen ist von Zähigkeit (Bakterien: ), die der grossen von Trägheit (Blauwal: ) bestimmt. (Ähnlichkeit)

Skalengesetze, biologische: Isometrie biologischer Zeiten T (T_L: Lebenszeit, T_W: Wachstum bis 50 % der Endgrösse; T_S: Schwangerschaft; T_bH: biologische Halbwertszeit (von Methotrexat), T_A: ein Atemzug, T_H: ein Herzschlag).

bottom:none;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'> TW / TL	TS / TL	TbH / TL	TA / TL	bottom:none;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'> TH / TL
bottom:solid black 1.0pt;border-right:none;mso-border-left-alt:solid black .75pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 3 × 10-2	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 1,5 × 10-2	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 1 × 10-5	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 3 × 10-9	bottom:solid black 1.0pt;border-right:solid black 1.0pt;mso-border-bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> 6,8 × 10-10

 

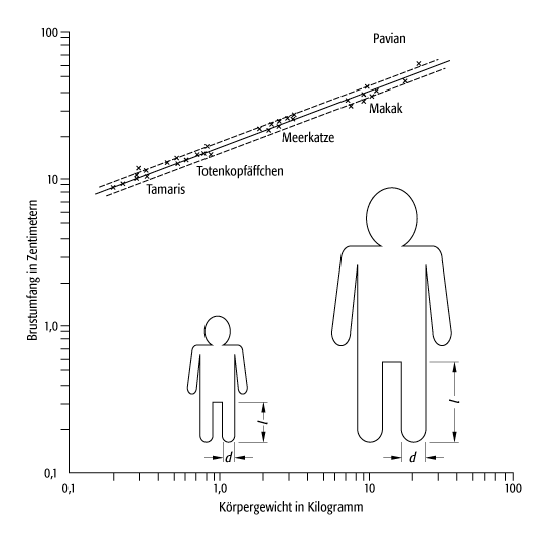
Skalengesetze, biologische 1: Allometrische Beziehung von Längs- und Quermassen (Figuren); der Brustumfang ergibt sich als propotional zur 0,37ten Potenz der Masse (Diagramm).

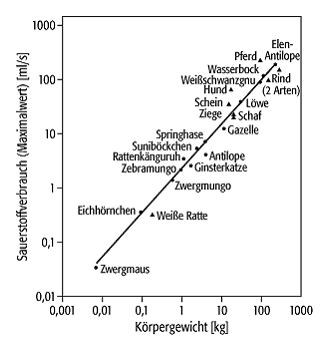
Skalengesetze, biologische 2: Das Gesetz von Kleiber für den Sauerstoffverbrauch pro Körpermasse bei Säugern; Steigung: 3 / 4 (theoretisch), 0,8 (experimentell).