Techniklexikon

Bernoullische Gleichung

Bernoullisches Theorem, nach D. Bernoulli benannte hydrodynamische Grundgleichung für stationäre, isentrope Strömungen:

Hierin bedeuten r die Dichte der strömenden Flüssigkeit,  die Strömungsgeschwindigkeit, w die spezifische Enthalpie, g die Gravitationsbeschleunigung und z die Höhe über einem willkürlich gewählten Nullniveau. Die Konstanz des Terms der linken Seite gilt längs einer Stromlinie; für verschiedene Stromlinien kann die Konstante verschiedene Werte annehmen. Die Bernoullische Gleichung kann durch eine Integration der Eulerschen Gleichungen für den Fall stationärer Strömungen abgeleitet werden.

Ist die Dichte r(p) bekannt, so lässt sich die Enthalpie  und damit die Bernoullische Gleichung explizit angeben (Tabelle). Beispiele hierfür sind

(i) die isotherme Zustandsänderung idealer Gase

 , also

(M = Molekulargewicht, R = allgemeine Gaskonstante, T = Temperatur);

(ii) die isentrope Zustandsänderung idealer Gase

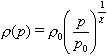, also

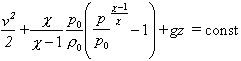
(mit k = Isentropenexponent).

Multipliziert man die Bernoullische Gleichung mit der Dichte r, so ist der Term auf der linken Seite eine Energiedichte (oder auch Druck), die sich aus der kinetischen Energiedichte  - auch dynamischer Druck oder Staudruck genannt -, dem Betriebsdruck p und der äusseren Potentialdichte rgz, dem Schweredruck, zusammensetzt; die Bernoullische Gleichung stellt also den Energieerhaltungssatz für ein Flüssigkeitselement dar, das sich im Fall einer stationären Strömung längs einer Stromlinie bewegt. Betriebsdruck und Schweredruck werden auch unter dem Namen statischer Druck zusammengefasst.

Wird zusätzlich zur Stationarität der Strömung vorausgesetzt, dass die Flüssigkeit inkompressibel ist, also r = const. gilt, so vereinfacht sich die Bernoullische Gleichung wegen  zu

Die Bernoullische Gleichung ist eine der am häufigsten angewandten Gleichungen der Strömungsmechanik, da sie den Energieerhaltungssatz für Flüssigkeiten ausdrückt. Wichtige Anwendungsbeispiele sind die Behandlung des hydrodynamischen Paradoxons, der Ausfluss aus Öffnungen sowie die Grundlagen für verschiedene Formen der Druckmessung in Strömungen. (Pitot-Rohr, Prandtlsches Staurohr) [CF]

Bernoullische Gleichung: Explizite Form der Bernoullischen Gleichung für verschiedene Strömungsarten. f(t) ist eine zeitabhängige Integrationskonstante, s ist der Weg, l der Widerstandsbeiwert, U der benetzte Umfang und A die Querschnittsfläche.

stationär inkompressibel
stationär inkompressibel reibungsbehaftet	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
stationär kompressibel	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
instationär- inkompressibel (verallgemeinerte Bernoullische Gleichung)	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>