Techniklexikon

relativistische Sterne

Relativitätstheorie und Gravitation, Sterne, deren Gravitationsfeld so stark ist, dass relativistische Effekte wichtig sind. Aus der inneren Schwarzschild-Metrik lässt sich die Oppenheimer-Volkoff-Gleichung ableiten:

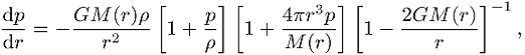
wobei  die Gravitationskonstante,  der innerhalb einer Kugel vom Radius  enthaltene Materieanteil,  der Druck und  die Dichte ist (die Einheiten seien so gewählt, dass  gilt). Die Oppenheimer-Volkoff-Gleichung ist die relativistische Verallgemeinerung der Gleichgewichtsbedingung zwischen Gravitationskraft und Druckkraft. Zur Lösung benötigt man noch die Zustandsgleichung .

Man kann ganz allgemein, unabhängig von der gewählten Zustandsgleichung, zeigen, dass sich bei nicht-variablem Radius, nicht-variabler Masse, Nicht-Singularität der Radius-Radius-Komponente der Metrik und von innen nach aussen nicht-ansteigender Dichte folgendes ergibt:

Dabei ist  der Sternradius und  die Gesamtmasse des Sternes. Es ergibt sich also bei gegebenem Radius eine Massenobergrenze bzw. bei gegebener Masse ein Mindestradius (der grösser als der Schwarzschild-Radius  ist).