Techniklexikon

Debyesche Theorie der Wärmekapazität

1912 von P. Debye begründete Theorie der spezifischen Wärmekapazität von Festkörpern. Diese Theorie geht von einem vereinfachten Modell des Festkörpers aus, der als isotropes elastisches Medium angesehen wird, das elastische Schwingungen in einem Frequenzintervall 0 £ w £ w₀ ausführen kann. Die Debye-Grenzfrequenz w_D ist dabei die Anzahl 3 N r der möglichen Gitterschwingungen, also die Anzahl der Bewegungsfreiheitsgrade eines Kristalls mit N Elementarzellen und r Atomen in der Elementarzelle. Aus heutiger Sicht entspricht dies sehr einfachen Annahmen für das Phononenspektrum aus (Phononen, Gitterschwingungen): Als erste Grundannahme ersetzt das Modell alle Zweige des Schwingungsspektrums durch drei. Für jeden dieser drei wird für die Phononenfrequenz w die gleiche lineare Dispersionsrelation w = c × k angenommen (k: der Wellenzahlvektor der Phononen, c: mittlere Schallgeschwindigkeit im Kristall, Dispersionsrelationen). Das Modell beschreibt demzufolge im wesentlichen nur akustische Phononen, während optische Phononen in dieses Bild nicht sinnvoll eingeschlossen werden können. Die zweite Grundannahme des Debye-Modells ist die Annäherung des Volumens der Brillouin-Zone durch das einer Kugel gleichen Rauminhalts (Debye-Kugel) mit dem Radius k_D (Debye-Radius). Um die korrekte Anzahl von Schwingungsmoden sicherzustellen, muss das Phononenspektrum bei einer maximalen Frequenz, der Debye-Grenzfrequenz w_D = c × k_D, abgebrochen werden. Die Phononenzustandsdichte g(w) im Debye-Modell erhält man aus

.

Hier ist (2p)³/V das Volumen eines Phononenzustands im k-Raum, V das Kristallvolumen und  das Volumen einer Kugelschale zwischen den Oberflächen k und k + dk; der Faktor 3 berücksichtigt die drei Zweige. Mit w = c × k ergibt sich g(w) zu

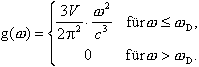
Die Gesamtenergie E der Gitterschwingungen ist . Darin steht n(w) für die Besetzungswahrscheinlichkeit eines Zustands mit der Energie  nach der Bose-Einstein-Verteilung. Unter Verwendung der Debye-Temperatur Q_D erhält man für den temperaturabhängigen Anteil von E:

mit  und k_B als Boltzmann-Konstante. Die Wärmekapazität C_V = ¶E/¶T ergibt sich somit zu

.

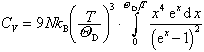Für hohe Temperaturen (T >> Q_D) tragen im Integranden nur sehr kleine x-Werte bei, so dass man e^x entwickeln kann, woraus man schliesslich das Dulong-Petitsche Gesetz c_V = 3 R erhält (c_V: molare spezifische Wärmekapazität, R: allgemeine Gaskonstante). Bei tiefen Temperaturen (T << V_D) ist die obere Grenze gross, man kann daher ohne grossen Fehler bis  ¥  integrieren und erhält für das Integral den konstanten Wert 4p⁴/15. Für C_V ergibt sich daraus

,

dies ist das experimentell gut bestätigte Debyesche T³-Gesetz.

Dieses Gesetz wird für sehr niedrige Temperaturen vom Experiment bestätigt und beschreibt das Verschwinden der spezifischen Wärmekapazität bei Annäherung an den absoluten Nullpunkt der Temperatur (Nernstsches Theorem). Die Debyesche Theorie der Wärmekapazität erweist sich als ausserordentlich nützliche einparametrige (Debye-Temperatur) Interpolation zwischen den beiden Grenzfällen hoher und niedriger Temperaturen, die bei tieferen Temperaturen genauer verläuft als die Einsteinsche Theorie der spezifischen Wärmekapazität (Einstein-Modell). Grössere Abweichungen treten bei Kristallen mit komplizierter, insbesondere mit stark anisotroper Kristallstruktur auf. In Metallen liefern die Elektronen einen zusätzlichen Beitrag zur spezifischen Wärmekapazität des Festkörpers.

Unterscheidet man die Beiträge, welche von den einzelnen akustischen Zweigen (transversale und longitudinale) zur spezifischen Wärmekapazität geliefert werden, so kann man ihnen im Modell des isotropen Kontinuums eigene Debye-Temperaturen q_p (mit p = 1, 2, 3) zuordnen. Die optischen Schwingungen, die im Phononenspektrum als Peaks sichtbar werden, können durch eine d-förmige Frequenzverteilung der Gitterschwingungen angenähert werden. Anisotrope Kristallstrukturen können approximativ durch richtungsabhängige Debye-Temperaturen erfasst werden. Schwierigkeiten des Debyeschen Modells, dem eine Kontinuumsvorstellung des Festkörpers zugrunde liegt, werden erst durch ein quantenmechanisches Herangehen überwunden.  [GR1, HW1]

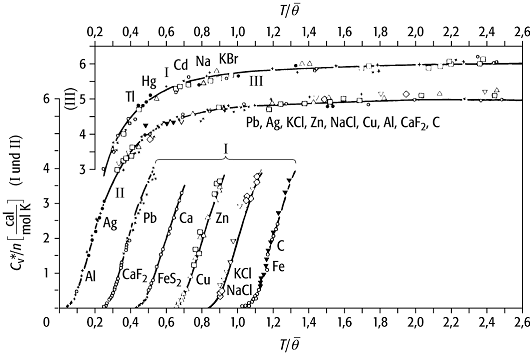
Debyesche Theorie der Wärmekapazität: Zur Erläuterung des Debye-Modells.