Techniklexikon

Quasikristalle und Quasielementarzellen

Festkörperphysik

bottom:.0001pt\'>1 Einleitung

bottom:.0001pt\'>Seit ihrer Entdeckung im Jahr 1984 stellen Quasikristalle ein verwirrendes Puzzlespiel dar: Warum bilden Atome ein komplexes, quasiperiodisches Muster anstelle einer regulären und sich wiederholenden Kristallanordnung? Die meisten Erklärungen dazu basieren auf Analogien mit sog. Tilings (Pflasterungen). So verfolgt z.B. das Penrose-Tiling-Bild das Konzept, dass sich Atome von selbst in zwei Cluster-Typen analog zu denen von stumpf- und spitzwinkeligen rhombischen Penrose-Tiles (Tiles sind eine Art Polygon oder Polytop) anordnen. Die Wechselwirkungen untereinander führen zu Verbindungen zwischen den Clustern, die den Penrose-Bildungsregeln (Matching Rules) für Tiles entsprechen. In einem anderen Modell, dem sog. Random-Tiling-Modell, wird die Struktur durch eine willkürliche Anordnung von zwei gleichen Tiles beschrieben, die der Quasikristall ohne Berücksichtigung der Bildungsregeln auf Grund der Entropie formt.

bottom:.0001pt\'>Die Vorstellung dieser Tiling-Modelle ist, dass die notwendigen Voraussetzungen zur Bildung eines Quasikristalles wesentlich komplexer sind als die zur Bildung eines Kristalles. So erscheint z.B. die Bedingung für das Auftreten von zwei Clustertypen notwendig, um Quasiperiodizität zu erhalten. Es ist jedoch schwer vorstellbar, dass es Energiebedingungen geben soll, die das Auftreten zweier Cluster im genau richtigen Dichteverhältnis erlauben (und andere Cluster ausschliessen), besonders unter dem Aspekt, dass die meisten bekannten Quasikristalle aus metallischen Elementen mit einem Zentralpotential und nicht starren kovalenten Bindungen bestehen. Im Fall des Penrose-Musters ergibt sich ein weiteres Problem, nämlich die Energiebedingungen zu finden, die durch die Matching Rules gegeben sind.

bottom:.0001pt\'>Eine sehr wichtige Entwicklung in der Beschreibung der atomaren Struktur von Quasikristallen war das Auftauchen des Quasielementarzellen (QEZ)-Modelles, das zum einen die Beschreibung der Struktur vereinfacht und zum anderen einen einfachen thermodynamischen Formalismus für die Quasikristallbildung vorschlägt. Im QEZ-Modell werden die Quasikristalle durch einen einzelnen sich wiederholenden Cluster beschrieben. Dieser sich wiederholende Cluster entspricht somit der Elementarzelle in einem periodischen Kristall. Das Neue an diesem Modell ist jedoch der Überlapp von benachbarten Cluster. Die Atome, die sich in der Überlappregion befinden, werden von zwei Clustern geteilt und bilden die hypothetischen Oberflächen, die den Clustern erlauben, sich gegenseitig zu durchdringen. Das Teilen der Atome bedeutet, dass es zu keiner Vervielfältigung oder Ansammlung dieser kommt. Das neue Bild besitzt keine einfache Interpretation in Bezug auf das Tiling, der Ausdruck Covering (Bedeckung) ist passender.

bottom:.0001pt\'>Verschiedene Modelle, die die Idee von überlappenden Clustern benutzen, sind in den letzten Jahren entwickelt worden. Aus Gründen der Bequemlichkeit bei der Analyse hat sich die Mehrzahl davon auf die dekagonale Phase konzentriert, die einen Quasikristall mit einer zehnfachen Symmetrie in der Ebene und einer periodischen Stapelung in der dritten Dimension beschreibt. Anhand von hochauflösenden Gitterbild-Untersuchungen an dekagonalem AlCuCo und AlNiCo zeigt sich, dass die atomare Struktur überlappende dekagonale Atomclustersäulen enthält. Es wurden verschiedene theoretische Modelle entwickelt, in denen die Atomstruktur vollständig durch einen einzigen sich wiederholenden dekagonalen Cluster und mit Hilfe von Überlappregeln beschrieben wird, die bestimmen, wie Nachbarcluster Bindungen miteinander eingehen. Diese frühen Modelle unterscheiden sich zwar in Einzelheiten voneinander, haben aber als gemeinsame Idee, dass durch die Überlappregeln keine eindeutige Struktur erzwungen wird. So wird z.B. im Modell von Burkov eine Struktur analog zu der eines binären Tilings erzeugt, in dem unendlich viele Anordnungen möglich sind [1]. Ähnliche experimentelle Beweise für sich überlappende Cluster wurden für ikosaedrische Quasikristalle gefunden. Janot schlug ein überlappendes Cluster-Modell zur Erklärung der Struktur und des Wachstums der ikosaedrischen Phase vor, indem er einen selbstähnlichen Wachstumsalgorithmus anstelle der Überlappregeln benutzte [2]. Ebenso wie Burkovs Modell erlaubt das selbstähnliche Wachstumsmodell neben einer periodischen und zufälligen Struktur auch eine perfekte quasiperiodische Struktur.

bottom:.0001pt\'>Das QEZ-Modell stellt gegenüber den frühen Ideen einen Fortschritt dar und entstand aus einem bemerkenswerten mathematischen Durchbruch: aus der Entdeckung, dass Cluster und Überlappregeln so gewählt werden können, dass man eine einzige und perfekt quasiperiodische Anordnung erhält, die isomorph zum Penrose-Tiling ist. Diese Entdeckung stürzte das bis dahin geltende Bild um, das auf der Penrose-Konstruktion basierte und besagte, dass zur Bildung einer perfekten Quasiperiodizität zwei Atomcluster notwendig sind. Anstelle der zwei inkommensurablen Längenskalierungen durch zwei Tile-Formen benutzt man nun die Längenskalierungen aus den Überlappregeln, die zwei unterschiedliche Nächste-Nachbarabstände zwischen den Clustern erlauben. Die Tatsache, dass beim Erzwingen einer einzigen Struktur die Überlappregeln ebenso wirken wie die Matching Rules, ist eine unvohergesehene Überraschung.

bottom:.0001pt\'>Das QEZ-Modell wurde erfolgreich in Studien an der dekagonalen Quasikristallphase von AlNiCo, einem der am besten experimentell charakterisierten Quasikristalle, getestet [3, 4]. Die Untersuchungen zeigen, dass die Struktur von AlNiCo in eine einzige, sich wiederholende dekagonale Clustersäule zerlegt werden kann, die in perfekter Übereinstimmung mit den Matching Rules die Atome mit den Nachbarn (bzw. den Überlappen) teilt. Die Untersuchung dieses Systemes stellt ein Modell für zukünftige quasikristalline Untersuchungen dar, die dann zu einem QEZ-Modell führen können.

bottom:.0001pt\'> 

bottom:.0001pt\'>2 Quasielementarzellen (QEZ)-Modell

bottom:.0001pt\'>Das QEZ-Modell schlägt vor, dass die Struktur eines Quasikristalles vollständig bestimmt ist durch einen einzigen, sich wiederholenden Cluster, der mit Nachbarclustern überlappt bzw. mit ihnen auf Grund einfacher Energiebedingungen die Atome teilt, so dass es zur Bildung einer einzigen perfekten quasiperiodischen Struktur kommt. Zunächst werden wir die Struktur in Form von ein wenig künstlich anmutenden Überlappregeln diskutieren, die die gleiche Rolle spielen wie die Penroseschen Edge-Matching-Rules bei der Bildung einer einzigen zum Penrose-Tiling isomorphen Struktur. Daran anschliessend wird diskutiert, wie die Überlappregeln durch physikalische Energiebedingungen ersetzt werden können.

bottom:.0001pt\'>Der Einfachheit halber betrachten wir den Fall eines dekagonalen Quasikristalles, dessen quasiperiodische Schichten die gleiche Symmetrie besitzen wie zweidimensionale Penrose-Tilings. Das zweidimensionale Analogon für das überlappende Clustermodell besteht aus zehneckigen Tiles, die so überlappen, dass sie eine zweidimensionale Fläche bedecken. Petra Gummelt mutmasste als erste, dass zehneckige Tiles mit entsprechend gewählten Überlappregeln ein perfekt quasiperiodisches Tiling formen können und entwarf den Beweis dazu [5]. Jeong und Steinhardt schlugen einen einfachen alternativen Beweis vor, der den Isomorphismus bezüglich des Penrose-Tilings mit zwei Tiles klärte [6].

bottom:.0001pt\'>Die von Gummelt und von Jeong und Steinhardt diskutierten zehneckigen Tiles sollen so verstanden werden, als ob sie endliche dekagonale Clustersäulen in der dreidimensionalen Quasikristall-Struktur darstellen, deren Höhe mit dem Wiederholungsabstand entlang der periodischen Richtung übereinstimmt. Der überlappende Cluster ist dann entsprechend den konventionellen Elementarzellen in einem perfekten periodischen Kristall als QEZ anzusehen. Allerdings ist im Unterschied zum Kristall die atomare Ausstattung der QEZ beschränkt: die Atomkonfiguration in einer QEZ muss die Eigenschaft besitzen, dass die benachbarten Cluster die Atome teilen können, ohne dass es zu einer signifikanten Störung ihrer Atomanordnung kommt.

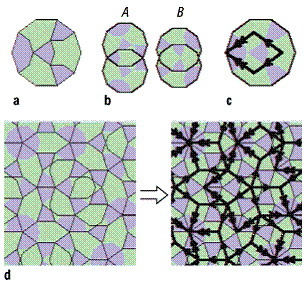
bottom:.0001pt\'>Die zehneckige QEZ ist in [31]Abb. 1 gezeigt. Die Anordnung besteht aus Kites (Drachen) und sternenähnlichen Formen, die als Gedächtnis für die Überlappregeln angeordnet sind. Um eine zum Penrose-Tiling isomorphe perfekte, quasiperiodische Bedeckung zu erzeugen, darf es den Zehnecken (wie in [32]Abb. 1b dargestellt) nur erlaubt sein, sich auf zwei Arten zu überlappen, nämlich als A- oder B-Typ. Mit Hilfe dieser Regeln überlappen drachenförmige Bereiche immer drachenförmige Bereiche und sternähnliche Bereiche immer sternähnliche Bereiche. Der Isomorphismus zwischen den Zehnecken und den Penrose-Tilings kann dadurch realisiert werden, dass jedes Zehneck mit einem grossen stumpfwinkeligen rhombischen Penrose-Tile versehen wird (markiert durch Einfach- und Doppelpfeile in [33]Abb. 1c). Als Folge dessen geht das Zehneck-Tiling aus [34]Abb. 1d in ein Penrose-Tiling über. In der Abbildung wurde dort Raum gelassen, wo spitzwinkelige Penrose-Rhomben eingeführt werden können.

bottom:.0001pt\'>Die Reduzierung eines Penrose-Tilings oder einer dekagonalen Phase auf einen einzelnen sich wiederholenden Cluster ist eine bemerkenswerte Vereinfachung. Im Fall der Atommodellierung bedeutet es, dass ähnlich wie im bekannten Fall der periodischen Kristalle die gesamte Struktur durch die atomare Anordnung der QEZ definiert ist. Bei der Erklärung, wieso es zur Bildung von Quasikristallen kommt, stellen die Überlappregeln einen lästigen Punkt dar, da sie komplizierte Energiebedingungen fordern. Infolgedessen ist eine weitere wichtige Entdeckung, dass weder die Matching-Rules noch die Überlappregeln berücksichtigt werden müssen. Stattdessen erhält man ein perfektes Penrose-Tiling, indem man die Dichte von einigen ausgewählten Atomclustern (C-Cluster) maximiert.

bottom:.0001pt\'>Um dieses Resultat zu illustrieren, idealisieren wir diese Diskussion dahingehend, dass wir Anordnungen aus spitz- und stumpfwinkeligen Rhomben annehmen, von denen jedes einen Atomcluster darstellt. Zusätzlich werden die Matching-Rules und die Überlappregeln vernachlässigt. Ohne weitere Einschränkungen existiert dann eine endliche Anzahl von sich unterscheidenden Tiling-Möglichkeiten, einschliesslich Penrose-, periodischem und Random-Tiling. Gibt es keine Energiebedingungen zur Unterscheidung zwischen diesen Möglichkeiten, so ist der Grundzustand entartet.

bottom:.0001pt\'>In realistischen Modellen ist es logisch anzunehmen, dass die Tiles Atomcluster darstellen und einige Tile-C-Cluster eine geringere Energie besitzen als andere. Dadurch kommt es zur Aufhebung der Entartung. Jeong und Steinhardt zeigten, dass für einen entsprechend gewählten C-Cluster das Penrose-Tiling als der einzige Grundzustand anzusehen ist. Stellt der gewählte Cluster aus Tiles einen energetisch bevorzugten Atomcluster dar, so führt die Minimierung seiner freien Energie zu einer Maximierung der Clusterdichte. Nach Jeong und Steinfeld ist das Penrose-Tiling die einzige Konfiguration, die eine maximale Dichte von C-Clustern besitzt.

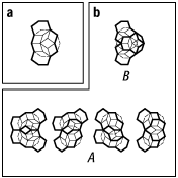
bottom:.0001pt\'>Eine von vielen verschiedenen Möglichkeiten für einen solchen C-Cluster ist in [35]Abb. 2 gezeigt. Zwei benachbarte C-Cluster können die Tiles miteinander teilen. Der grösste Überlapp entspricht genau dem A- und B-Überlapp des zentralen zehneckigen Bereiches von C. Es ist klar, dass der C-Cluster durch die bereits beschriebene dekagonale Bedeckung hervorgerufen wird, auch wenn die genaue Beziehung relativ subtil ist. Das nicht triviale Ergebnis ist, dass die Maximierung der C-Clusterdichte automatisch zu einer Struktur führt, in der die C-Cluster im Verhältnis 1:1 zu den QEZ in einem einzigen Zehneck-Tiling stehen. Im speziellen Fall, dass alle Anordnungen aus spitz- und stumpfwinkeligen Tiles bestehen, stellt das Penrose-Tiling die einzige Anordnung von C-Clustern dar, in der jeder C-Cluster einen A- oder B-Überlapp mit seinem Nachbarn hat. Jeong und Steinhardt haben zusätzlich gezeigt, dass der Grundzustand für einen weiten Bereich der Energiezuordnung der Cluster eindeutig bleibt.

 

3 Neuere Experimente

Um neben den abstrakten Untersuchungen der Tilings weitere Fortschritte zu erzielen, müssen Beispiele von real existierenden Quasikristallen gefunden werden, die das QEZ-Modell unterstützen. Dafür wäre besonders ein solcher Quasikristall geeignet, der eine einfache QEZ-Ausstattung besitzt, so dass diese Übereinstimmung deutlich wird. Einen Durchbruch stellen die neueren Untersuchungen der dekagonalen Phase von AlNiCo dar [3, 4]. Diese Untersuchungen zeigen eine hervorragende experimentelle Übereinstimmung mit dem QEZ-Modell.

Hochauflösende Gitterbilder enthüllen einen Netzwerk von sich überlappenden zehneckigen Clustersäulen mit einem Durchmesser von 2 nm. Die schon historischen Schwierigkeiten mit AlNiCo, die Unordnung und die Supergittereffekte, vereiteln allerdings eine strukturelle Analyse. Frühe Modelle wie das von Burkov zur Beschreibung des Quasikristalles mit Hilfe von sich überlappenden Clustern mit einer dekagonalen oder pentagonalen Symmetrie benutzten Überlappregeln, die Random-Tilings produzierten. Das Random-Tiling-Bild erscheint angemessen, da es den Experimenten Hinweise auf diffuse Streuung gibt.

Vor kurzem fanden jedoch Tsai und Mitarbeiter eine einfache dekagonale Phase von in Wasser gequenchtem Al₇₂Ni₂₀Co₈, welches keine durch ein Supergitter hervorgerufene Reflexionen oder diffuse Streifen besitzt [7]. [36]Abb. 3 zeigt eine Superposition eines HAADF (high angle annular dark-field)-Bildes für Al₇₂Ni₂₀Co₈ von Saitoh und Mitarbeitern [8] und eines einzigen Zehneck-Tilings. Die hellen Punkte in der HAADF-Darstellung entsprechen der Position der Übergangsmetallatome. Wird das Bild bei einem bestimmten Winkel festgehalten, so erkennt man, dass das Gitterbild über eine Strecke von fast 15 nm keine beobachtbare Phasonverzerrung besitzt, es also isomorph zu einem perfekten Penrose-Tiling ist. Ausserdem scheint die Struktur aus sich überlappenden dekagonalen Clustern zu bestehen. Im HAADF-Bild in [37]Abb. 4 erkennt man, dass der innerste Atomring im Cluster weder fünf- noch zehnfache Symmetrie besitzt. Vielmehr bricht die Struktur die dekagonale Symmetrie genau so wie die Überlappregeln (siehe dazu die superpositionierten Kite-förmigen Dekorationen auf den dekagonalen Tiles). Mit konvergenter Elektronenstrahlbeugung kann die Raumgruppe als punktsymmetrische P10₅ / mmc bestimmt werden.

bottom:.0001pt\'>Die vielversprechende Beobachtung von überlappenden Clustern in Al₇₂Ni₂₀Co₈ erlaubt einen detaillierten Vergleich mit dem QEZ-Modell [3, 4]. In [38]Abb. 3 ist das Gitterbild mit einem einzelnen perfekten Zehnfach-Tiling überlagert. Die perfekte Tiling-Überlagerung ist in [39]Abb. 5 dargestellt. Die Übereinstimmung ist nahezu über das gesamte Bild perfekt und die Atomausstattung jedes Zehnecks und jede drachenförmige Dekoration innerhalb des Zehnecks erscheinen identisch.

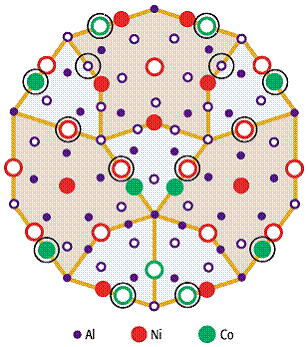
bottom:.0001pt\'>In [40]Abb. 6 ist eine Möglichkeit der atomaren Anordnung einer dekagonalen Elementarzelle vorgestellt, die mit aktuellen Messungen übereinstimmt: die Stöchiometrie Al_71,3Ni_20,5Co_9,2 und die Dichte 3,98 g / cm³ weichen lediglich um 1 % von den gemessenen Werten ab, das berechnete HREM-Gitterbild zeigt eine sehr gute Übereinstimmung mit dem experimentell ermittelten. Infolgedessen erscheint Al₇₂Ni₂₀Co₈ als ein Kandidat, für den die Zehneck-These nachgewiesen und im Detail untersucht werden kann.

 

4 Folgerungen

Das QEZ-Modell, das sich aus neuesten mathematischen Entdeckungen über die Penrose-Tilings entwickelt hat und durch experimentelle Beweise gestützt wird, erlaubt neue Einblicke in die Struktur, die Stabilität und das Wachstum von Quasikristallen. Die atomare Struktur eines Quasikristalles kann vollständig anhand der Ausstattung eines einzelnen Clusters charakterisiert werden. Dieses Ergebnis vereinfacht das Problem der Spezifizierung und der Bestimmung der atomaren Struktur, solange die einzigen Freiheitsgrade die Atomarten und die Positionen innerhalb der Quasielementarzelle sind. Jede atomare Anordnung eines konventionellen Penrose-Tilings kann also als durch die atomare Anordnung der QEZ interpretiert werden - allerdings gilt die Umkehrung nicht. Manche Anordnungen der QEZ sind nicht äquivalent zu denen, die man erhält, wenn man stumpf- und spitzwinklige Tiles jeweils identisch anordnet. In diesem Sinn besitzt das QEZ-Modell mehr Möglichkeiten als das frühere Penrose-Tiling-Bild.

Ein anderer Aspekt ist, dass die atomare Anordnung der QEZ die Symmetrie der Struktur verschlüsselt. In der Vergangenheit wurde die Symmetrie unter Berufung auf den reziproken Raum oder eine Projektion von einem fünf- oder sechsdimensionalen periodischen Gitter bestimmt. Mit Hilfe des QEZ können diese indirekten Techniken durch eine Beschreibung des realen Raumes ersetzt werden. Es existiert eine leicht zu verstehende Übereinstimmung zwischen der atomaren QEZ-Dekoration im realen Raum und der Gruppensymmetrie der Struktur.

Die QEZ-Näherung setzt eine enge physikalische Verbindung zwischen Quasikristall und Kristall voraus. Es wird nun deutlich, dass beide in Form der dichtesten Packung eines einzelnen Clusters oder einer QEZ beschrieben werden können. In einem Kristall sind die Elementarzellen Kante an Kante gepackt. Quasikristalle entsprechen einer Verallgemeinerung, in der sich die Elementarzellen überlappen. In beiden Fällen kann die Bildung einer speziellen Struktur mit Hilfe eines niederenergetischen Clusters erklärt werden, obwohl sich im Fall der Quasikristalle die atomaren Anordnungen überlappen müssen. Damit lässt sich erklären, wieso Quasikristalle weniger häufig sind als Kristalle.

Es fehlt nun noch die Erkärung des Wachtumsmechanismus der Quasikristalle. Sind die Quasikristalle langsam aufgewachsen, so ist eine thermodynamische Relaxation in den Grundzustand möglich. Allerdings werden einige der perfektesten Quasikristalle wie z.B. Al₇₂Ni₂₀Co₈ durch schnelles Quenchen erzeugt. Das QEZ-Modell liefert dazu zwei Vermutungen: Unter der Annahme, dass der einer QEZ entsprechende atomare Cluster energetisch bevorzugt wird, folgt zum einen, dass die Überlappregeln nahelegen , dass jeder Cluster den Keim für einen neuen Nachbarcluster enthält, da die enthaltenen Atome letztendlich alle geteilt werden. Man kann sich vorstellen, dass örtlich neue Cluster aus schon existierenden entstehen, solange diese energetisch bevorzugt sind und einen Keim besitzen. Zum anderen entspricht, wie bereits erwähnt, dem idealen Quasikristall ein Maximum in der Clusterdichte. Wird der Cluster also energetisch bevorzugt, dann erscheint es nur natürlich, dass das System wächst, indem ein Cluster an den anderen gefügt wird und es so zu einer Maximierung der lokalen Dichte kommt. Diese Argumente können die Bildung von hoch perfekten Quasikristallen erklären.

Das Bild sich überlappender Cluster könnte auch zur Erklärung anderer physikalischer Eigenschaften der Quasikristalle herangezogen werden, z.B. der Eigenschaften der inelastischen Neutronenstreuung und des Verhaltens der elektrischen und thermischen Leitfähigkeit.

Abschliessend ist zu sagen, dass das QEZ-Modell ein wenig Licht in ein altes Geheimnis bringt und eine natürliche und allgemeine Erklärung dafür liefert, warum es zur Bildung von Quasikristallen kommt. Das Problem wird dabei reduziert auf das Verhalten kleiner atomarer Cluster und die gemeinsame Benutzung der Atome durch die Cluster. Eventuell können in der Zukunft Gesamtenergieberechnungen basierend auf einer kleinen Anzahl von Atomen benutzt werden, um die Bildung von Quasikristallen zu verstehen und bei der Vorhersage neuer Arten zu helfen. Anhand zukünftiger struktureller und kinetischer Untersuchungen an schon bekannten Quasikristallen wie z.B. AlNiCo können diese Prinzipien gefestigt werden und schliesslich zu einem neuen Verständnis für und eine bessere Kontrolle über die Struktur und die Bildung von Quasikristallen führen.

 

Literatur:

[1] S. Burkov, J. Phys. 2, 695 (1992); Phys. Rev. Lett. 67, 614 (1991).

[2] C. Janot und J. Patera, Phys. Lett. A233, 110 (1997).

[3] P.J. Steinhardt, H.-C. Jeong, K. Saitoh, M. Tanaka, E. Abe und A.P. Tsai, Nature 396, 55 (1998).

[4] E. Abe, K. Saitoh, H.H. Takakura, A.P. Tsai, P.J. Steinhardt und H.-C. Jeong, Preprint cond-mat/9907160.

[5] P. Gummelt, Geomitriae Dedicata 62, 1 (1996).

[6] P.J. Steinhardt und H.-C. Jeong, Nature 392, 433 (1996).

[7] A.P.Tsai, A. Fujiwara, A. Inoue und T. Masumoto, Phil. Mag. Lett. 74, 233 (1996).

[8] K. Saitoh, K. Tsuda, M. Tanaka, K. Kaneko und A.P. Tsai, Jpn. J. Appl. Phys. 36, L1400 (1997).

Quasikristalle und Quasielementarzellen 1: Eine quasiperiodisches Tiling kann durch die in a) gezeigten markierten Zehnecke erzeugt werden. b) Die Matching-Rules fordern, dass zwei Zehnecke nur dann überlappen, wenn die schattierten Bereiche überlappen. Daraus ergeben sich die beiden Möglichkeiten, dass der Überlappbereich entweder sehr klein (Typ A) oder sehr gross (Typ B) ist. Ist jedes Dekagonal mit einem grossen stumpfwinkeligen Rhombus wie in c) versehen, so wird das Tiling der sich überlappenden Zehnecke (d, links) in ein Penrose-Tiling (d, rechts) übergehen.

Quasikristalle und Quasielementarzellen 2: Unter der Annahme spitz- und stumpfwinkeliger Rhomben und Vernachlässigung der Matching-Rules stellt das Penrose-Tiling die Konfiguration mit der höchsten Dichte von C-Clustern dar. a) C-Cluster: wird das Zehneck im Zentrum von sieben Rhomben umgeben (gepunktete Linie), so formen die Zehnecke ein überlappendes Zehneck-Tiling. b) Die beiden Arten des Überlappes zwischen den C-Clustern, die die Zentren der C-Cluster näher zusammen bringen. (Die A-Typen besitzen die gleiche Trennung zwischen den Zentren). Sind die Zehnecke um die zentralen sieben Rhomben gruppiert, so gehen die A- und B-Typ-Überlappe zwischen den C-Clustern in präzise A- und B-Typ-Überlappe zwischen den Zehnecken in der QEZ-Beschreibung über.

Quasikristalle und Quasielementarzellen 3: Die Superposition eines perfekten Zehneck-Tilings mit einem HAADF-Gitterbild von in Wasser gequenchtem Al₇₂Ni₂₀Co₈. Das Überlapp-Zehneck-Tiling ist getrennt in Abb. 5 gezeigt. Zu beachten ist der hohe Grad der Ordnung im Gitterbild und die fast perfekte Übereinstimmung mit den überlagerten Zehnecken.

Quasikristalle und Quasi-Einheitszellen 4: Die Vergrösserung eines Zehneck-Clusters in wassergequenchtem Al₇₂Ni₂₀Co₈ mit der HAADF-Methode. Das Zehneck besitzt eine Grösse von ca. 2 nm. Die Überlagerung zeigt zur Darstellung der Überlappregeln eine einzige dekagonale QEZ mit eingezeichneter dekagonaler Symmetriebrechung.

Quasikristalle und Quasi-Einheitszellen 5: Das Tiling mit einem einzigem Zehneck, das in Abb. 3 zur Überlagerung des HAADF-Gitterbildes benutzt wurde.

Quasikristalle und Quasielementarzellen">

bottom:.0001pt;border:none; padding:0cm\'>Quasikristalle und Quasi-Einheitszellen 6: Ein mögliches Modell zur Beschreibung der Atomverteilung einer dekagonalen QEZ für Al₇₂Ni₂₀Co₈. Die grossen Kreise stellen Ni oder Co dar, die kleinen Kreise repräsentieren Al. Die offenen Kreise beschreiben die Atome in der fundamentale Zehneck-Anordnung. Bei einer Überlappung der Nachbarn werden die Atome durch schattierte Kreise gekennzeichnet. Bei diesen Atomen zeigt sich von Zehneck zu Zehneck eine Variation in Abhängigkeit vom speziellen Überlapp der Nachbarn. Die Struktur besitzt zwei ausgeprägte Lagen entlang der periodischen c-Achse. Die schattierten Kreise liegen bei c = 0 und die offenen Kreise bei c = 1/2.