Techniklexikon

Tolman-Oppenheimer-Volkoff-Gleichung

Relativitätstheorie und Gravitation, Oppenheimer-Volkoff-Gleichung, beschreibt das relativistische Gleichgewicht zwischen Druck und Gravitation in sphärisch-symmetrischen Sternen. Sie wurde in den dreissiger Jahren von Oppenheimer, Tolman und Volkoff aufgestellt und lautet:

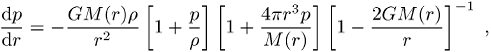 wobei  die Gravitationskonstante,  der innerhalb einer Kugel vom Radius  enthaltene Materieanteil,  der Druck und  die Dichte ist (die Einheiten seien so gewählt, dass  gilt).

Um sie herzuleiten, betrachtet man eine statische, sphärisch-symmetrische Materieverteilung. Dann hat die Metrik in geeigneten Koordinaten folgende allgemeine Form:

Die Materie werde durch den Energie-Impuls-Tensor einer perfekten Flüssigkeit beschrieben. Löst man nun die Einstein-Gleichungen für die hier beschriebene Situation, so erhält man nach einigen einfachen Umformungen die Oppenheimer-Volkoff-Gleichung. Im nicht-relativistischen Grenzfall gilt: ,  und die Oppenheimer-Volkoff-Gleichung geht über in die Newtonsche Gleichgewichtsbedingung:

 (Newtonsche Sterne, relativistische Sterne)