Techniklexikon

Chaoskontrolle

Methode zur Überführung chaotischen Verhaltens (Chaos) eines Systems in eine stabile, periodische Bewegung durch kleine Änderungen der Systemparameter. Die bekannteste Methode, das OGY-Verfahren, ist nach E. Ott, C. Grebogi und J.A. Yorke benannt. Dort wird die Existenz einer stabilen Mannigfaltigkeit W ^S und eines instabilen periodischen Orbits W ⁱ ausgenützt, indem eine chaotische Trajektorie durch kleine Parameteränderungen auf diese Mannigfaltigkeit gelenkt wird, so dass sie von dem entsprechenden instabilen periodischen Orbit angezogen wird. Diese Vorgehensweise ist in der Figur für die Stabilisierung eines Fixpunktes z^*(m) bei einem Systemparameter m Î  einer 2-dimensionalen iterierten Abbildung  mit  dargestellt. Als explizite Formel für die durchzuführende Parameter-Änderung ergibt sich hier

.

Dabei ist e_i Î ² ein Vektor, der im Punkt z*(m) auf der stabilen Mannigfaltigkeit W ^S(m) senkrecht steht, l_i der instabile, d.h. grössere Eigenwert der Matrix  und ¶_m die partielle Ableitung nach der Variablen m. Es werden also die Lage des anvisierten periodischen Orbits und die linearisierten Bewegungsgleichungen in seiner Nähe benötigt. Letztere können z.B. mittels einer Attraktor-Rekonstruktion aus einer experimentellen Zeitreihe gewonnen werden. Da die Formel für die Parameter-Änderung dm auf einer Linearisierung beruht, fällt der Punkt z _t+1(m + dm) i.a. nicht exakt auf die stabile Mannigfaltigkeit W^s(m), so dass in jeder weiteren Iteration t kleine Parameter-Änderungen  notwendig werden. Aus demselben Grund wird die Kontrollprozedur nur eingeschaltet, wenn eine chaotische Trajektorie z^*(m) einen gewissen Mindestabstand von der stabilen Mannigfaltigkeit einnimmt. Letzteres tritt wegen des ergodischen Verhaltens (Ergodentheorie) auf einem Attraktor oder in einer ergodischen Komponente des Systems immer wieder ein. Der Orbit des Systems bei eingeschalteter Kontrolle ist ein Beispiel für eine chaotische Transiente. Die Verallgemeinerung der beschriebenen Prozedur auf höher-dimensionale oder zeitkontiniuerliche Systeme basiert auf bekannten Methoden der Kontrolltheorie.

Eine alternative Methode zur Stabilisierung instabiler periodischer Orbits in chaotischen Systemen benutzt eine zeitverzögerte Rückkopplung des Systemzustandes auf die Systemparameter. In einem zeitlich kontinuierlichen System, z.B. , wird die rechte Seite dabei durch  mit einer Verzögerungszeit t ersetzt, wobei  gelten muss.

In beiden Fällen können, da instabile periodische Orbits auf einem chaotischen Attraktor (für dissipative Systeme) oder in einem chaotischen See (fast-integrable Systeme) typischerweise dicht liegen, die vielfältigsten periodischen Bewegungen stabilisiert werden. [GR2]

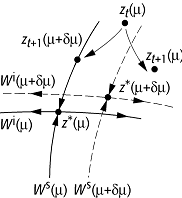
Chaoskontrolle: Erläuterung im Text.