Techniklexikon

kanonische Quantisierung

Quantisierungsschema, das die formale Korrepondenz (Korrespondenzprinzip) zwischen klassischer und Quantenmechnik nutzt. Im Einteilchen-Fall (erste Quantisierung) werden dabei die verallgemeinerten Koordinaten q_i und p_i durch entsprechende Operatoren, welche die Vertauschungsrelation zur gleichen Zeit

erfüllen, ersetzt. In der Quantenfeldtheorie (zweite Quantisierung) geht man analog vor: Die Zeit wird als spezielle Koordinate ausgezeichnet, zu dem (im einfachsten Fall skalaren) Feld  wird das konjugierte Feld

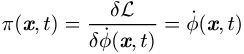
und damit die Hamilton-Dichte

gebildet;  und  erfüllen analog zur klassischen Mechanik die Vertauschungsrelation(alle anderen Kommutatoren verschwinden). Eine Möglichkeit, diese Relation zu erfüllen, besteht in der Wahl einer Fourier-Darstellung mit ebenen Wellen für  und ,

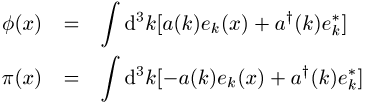
mit .  und  lassen sich als Erzeugungs- und Vernichtungsoperatoren interpretieren, d.h.  definiert einen Einteilchen-Zustand; im Unterschied zur ersten Quantisierung lassen sich nun aber auch Mehrteilchenzustände erzeugen,

Für fermionische Felder läuft die Quantisierung entsprechend, nur dass für das Dirac-Feld  und die vier Operatoren  ( ist der Erzeugungsoperator für Antiteilchen, also Positronen) anstelle der Vertauschungsrelationen Antikommutatoren verwendet werden. Die Antivertauschungsrelationen reproduzieren das Pauli-Prinzip: wegen  kann immer nur ein Teilchen einen Energiezustand mit defniertem Spin besetzen. Ein fermionischer Mehrteilchenzustand ist somit gegeben durch

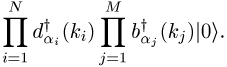
Die kanonische Quantisierung ist das direkteste Quantisierungsprogramm. Es hat den Nachteil, durch die Auszeichnung der Zeit die Lorentz-Invarianz zu verletzen; dafür quantisiert es (im Unterschied zum Gupta-Bleuler-Formalismus) nur physikalische Zustände.