Techniklexikon

Feynman-Diagramm

Teilchenphysik, Feynman-Graph, wichtiges Werkzeug der Quantenfeldtheorie, das es ermöglicht, alle Terme der störungstheoretischen Entwicklung der S-Matrix zu konstruieren und zu berechnen. Dazu wird aus den beiden Termen nullter und erster Ordnung der Störungsreihe ein Katalog sog. Feynman-Regeln zusammengestellt, der sowohl die Konstruktionsvorschrift für die Diagramme höherer Ordnung enthält als auch die Rechenvorschrift für die Amplitude des entsprechenden Wechselwirkungsprozesses. Hat man also diesen Regelkatalog einmal für eine bestimmte Wechselwirkung abgeleitet, lässt sich in jeder Ordnung das vollständige Set der zu berechnenden Beiträge zu einem bestimmten Prozess angeben, ohne jedesmal die gesamte Quantisierungsprozedur und die Störungsentwicklung durchführen zu müssen.

Feynman-Diagramme stellen die Wechselwirkungen von Elementarteilchen in einem Koordinatensystem mit Zeit und Ort dar. Dabei treten drei Bestandteile auf: 1) Ein- und auslaufende reelle Teilchen, 2) innere virtuelle Teilchen, z.B. ausgetauschte Eichbosonen, denen Propagatoren zugeordnet werden, und 3) Schnittpunkte von Linien (Vertizes), die die Kopplungspunkte der beteiligten Teilchen repräsentieren. Die Anzahl der Vertizes eines Diagramms repräsentiert seine entsprechende störungstheoretische Ordnung. Strahlungskorrekturen, also Beiträge höherer Ordnung der Störungsreihe, werden in Feynman-Diagrammen durch Schleifen (engl. loops) dargestellt, über deren umlaufenden Impuls integriert werden muss.

Unter allen möglichen Feynman-Diagrammen sind die Ein-Teilchen-irreduziblen (engl. one-particle irreducible, abgekürzt 1PI) Feynman-Diagramme besonders ausgezeichnet. Bei ihnen ist es nicht möglich, den Graphen durch das Durchschneiden einer inneren Linie in zwei Teile zu zerlegen. Die Beiträge dieser Diagramme zu den Fermion- und Eichbosonpropagatoren werden Selbstenergien genannt. Es lässt sich zeigen, dass die vollen Propagatoren inklusive aller Strahlungskorrekturen durch Selbstenergien konstruiert werden können.

Die Diagrammtechnik wurde von R. Feynman ursprünglich in der Quantenelektrodynamik (QED), der einfachsten Quantenfeldtheorie des Standardmodells, benutzt. In der niedrigsten Ordnung der Störungsentwicklung tritt in der QED nur der elementare Elektron-Photon-Vertex auf (Abb. a). Zu den Diagrammen zweiter Ordnung zählen neben den Streudiagrammen (Abb. b, c, d) die Selbstenergien mit einer Schleife (Abb. e). Ihre Berechnung führt auf divergente Ausdrücke, die durch eine Renormierung der in die Diagramme eingehenden Parameter (Massen, Kopplungskonstanten) endlich gemacht werden können.

Starke und schwache Wechselwirkung erzeugen eine Vielzahl weiterer Feynman-Diagramme. Die nichtabelsche Struktur der entsprechenden Theorien ermöglicht dabei auch Kopplungen der Eichbosonen untereinander. Die Konstruktions- und Berechnungsprinzipien der Diagramme bleiben aber im wesentlichen unverändert. [UK]

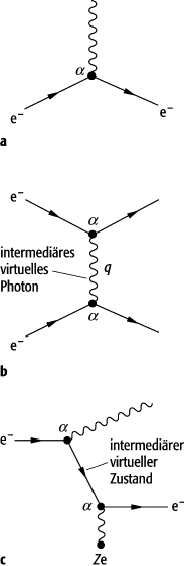
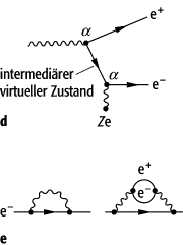
Feynman-Diagramm: a) Diagramm, das der niedrigsten Ordnung der Störungsentwicklung der QED entspricht; es tritt nur der elementare Elektron-Photon-Vertex auf. b), c), d) Streudiagramme zweiter Ordnung; e) Selbstenergiediagramme.