Techniklexikon

Robertson-Walker-Metrik

Relativitätstheorie und Gravitation, die Metrik einer homogenen und isotropen Raumzeit. In der Kosmologie ist die Robertson-Walker-Metrik von besonderer Bedeutung, da sie die Kinematik derjenigen kosmologischen Modelle beschreibt, die dem kosmologischen Prinzip gehorchen, das einen homogen-isotropen Kosmos fordert und durch viele Beobachtungsdaten getragen wird, etwa durch die ausserordentliche Isotropie der kosmischen Hintergrundstrahlung. Die 1929 von H.P. Robertson und 1936 von A.G. Walker bestimmte Metrik

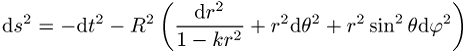
ist durch die zeitabhängige Skalenfunktion R(t) und die Konstante metrik.gif" alt="Robertson-Walker-Metrik"> charakterisiert. Die dreidimensionalen Raumschnitte t = const. sind Räume konstanter Krümmung, die durch den Wert von k bestimmt sind:  beschreibt einen Raum konstanter negativer Krümmung,  einen flachen Raum und  einen Raum konstanter positiver Krümmung. Die Entwicklung der Skalenfunktion R(t), die die zeitliche Expansion bzw. Kontraktion der dreidimensionalen Raumschnitte beschreibt, in die Taylor-Reihe

mit , definiert die Koeffizienten . Dabei ist  die n-te zeitliche Ableitung der Skalenfunktion und . Die Grössen H und metrik.gif" alt="Robertson-Walker-Metrik"> sind die (zumindest im Prinzip) in jeder kosmologischen Epoche beobachtbaren Parameter der Dimension metrik.gif" alt="Robertson-Walker-Metrik"> und . H(t) ist die Hubble-Funktion, und der Wert der Hubble-Funktion in der heutigen Epoche t(0) ist die Hubble-Konstante H₀,  der Akzelerationsparameter. In der Allgemeinen Relativitätstheorie ist die Dynamik der Robertson-Walker-Geometrie durch Einsetzen der Metrik in die Einstein-Gleichungen bestimmt. Die Lösungen der resultierenden Friedmann-Gleichungen bilden die Familie der Friedmann-Modelle des Universums. Dazu gehören u.a. der Einstein-Kosmos (1917), der Einstein-de-Sitter-Kosmos (1932) und der Lemaître-Kosmos (1935).