Techniklexikon

Strahlungsgesetze

Optik, Sammelbegriff für Gesetze der Temperaturstrahlung in Abhängigkeit von der absoluten Temperatur T und der Frequenz n bzw. der Wellenlänge l. Kirchhoff leitete 1859 aus allgemeinen thermodynamischen Prinzipien das nach ihm benannte Strahlungsgesetz ab, welches das Strahlungsvermögen von Volumen- und Oberflächenstrahlern beschreibt und besagt, dass das Verhältnis aus spektraler Strahldichte und spektralem Absorptionsgrad bei gleicher Frequenz n und absoluter Temperatur T für alle Körper konstant und gleich der spektralen Strahldichte des schwarzen Körpers ist. Absorbiert ein Körper bei einer Wellenlänge stark, so emittiert er dort auch stark. Die grösste Spektraldichte hat demnach der schwarze Körper mit einem spektralen Absorptionsgrad a(n, T) von Eins. Die erste Gesetzmässigkeit der schwarzen Strahlung wurde von Stefan gefunden und beinhaltet die Proportionalität zwischen der Gesamtstrahlung des schwarzen Körpers und der vierten Potenz der absoluten Temperatur T. Boltzmann fand diesen Zusammenhang ebenfalls, indem er den von der Maxwellschen Theorie gelieferten Zusammenhang zwischen dem Strahlungsdruck p und der Energiedichte u für ungerichtete Strahlung benutzte (p = u / 3) und auf einen von Strahlung erfüllten Hohlraum die gleichen thermodynamischen Überlegungen anwandte wie auf ein von einem wirklichen Gas erfülltes Volumen. Das sogenannte Stefan-Boltzmann-Gesetz erlaubt die Berechnung der Gesamtemission des schwarzen Strahlers über den gesamten Frequenzbereich und lautet

Die Konstante b = 5,67 10^-8 W / (m² K⁴) wird als Stefan-Boltzmann-Konstante bezeichnet. Schon eine geringe Erhöhung der Temperatur führt zu einer beträchtlichen Zunahme der Emission. Das Stefan-Boltzmann-Gesetz wurde durch Messungen von Lummer und Pringsheim am schwarzen Körper quantitativ bestätigt; sie zeigten damit nachträglich die Berechtigung der Übertragung thermodynamischer Prinzipien auf Strahlungsfelder.

Zwei wichtige Schritte bis zur Auffindung des endgültigen Strahlungsgesetzes durch Planck waren die einerseits von Rayleigh und Jeans und andererseits von Wien aufgestellten Formeln. Auf Anregung durch Rayleigh berechnete Jeans die Zahl der elektromagnetischen Eigenschwingungen, die in einem mit Strahlung erfüllten Hohlraum mit spiegelnden Wänden auftreten (Hohlraumstrahlung). Aus dem sogenannten Rayleigh-Jeans-Gesetz folgt für die spektrale Energiedichte

wobei k die Boltzmann-Konstante und c die Lichtgeschwindigkeit ist. Unabhängig davon griff Wien den Gedanken von Boltzmann auf und verfeinerte die Analogie zwischen der Thermodynamik eines Gases und eines Strahlungsfeldes dahingehend, dass er der Strahlung nicht nur eine Energie, sondern auch eine Entropie zuschrieb. Daraus ergibt sich ein weiterer wichtiger Zusammenhang zwischen der spektralen Energiedichte u, der Frequenz n und der Temperatur T eines schwarzen Strahlers:

Es zeigt sich, dass beide Formeln nur in bestimmten Grenzbereichen Gültigkeit haben. Gemäss dem Rayleigh-Jeans-Gesetz steigt die Energiedichte proportional zum Quadrat der Frequenz an, und für grosse Frequenzen (im Ultravioletten und im Röntgenbereich) müsste die Energiedichte die Strahlers unendlich gross werden (Ultraviolettkatastrophe). Dagegen haben experimentelle Untersuchungen gezeigt, dass für kleine Frequenzen die Rayleigh-Jeans-Formel zur Berechnung der Energiedichte gut geeignet ist. Im Gegensatz dazu findet das Wiensche Gesetz seine Bestätigung im Bereich grosser Frequenzen, versagt aber völlig bei kleinen Frequenzen.

Erst Planck gelang schliesslich im Jahr 1900 die Auffindung der vermittelnden Formel (Plancksche Strahlungsformel)

Revolutionär war bei der Herleitung des Strahlungsgesetzes durch Planck der Gedanke, dass die Strahlung von einem Temperaturstrahler nicht kontinuierlich, sondern in Quanten der Grösse hn ausgesendet wird. Gemäss dem Gleichverteilungssatz der klassischen Elektrodynamik entfällt auf jeden Freiheitsgrad der Schwingung nicht mehr wie von Rayleigh-Jeans angenommen die gleiche mittlere Energie kT (d.h. kT / 2 für die kinetische und kT / 2 für die potentielle Energie), sondern die mittlere Energie

die im Gegensatz zum klassischen Ausdruck von der Frequenz n abhängt. Für hohe Temperaturen geht dieser Wert jedoch in den klassischen von kT über, somit behält der Gleichverteilungssatz seine Gültigkeit. Die von Planck aufgestellte Quantenhypothese zur Herleitung seines Strahlungsgesetzes stellt das Fundament der Quantentheorie dar.

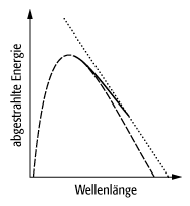
Strahlungsgesetze: Das Wiensche Strahlungsgesetz (gestrichelte Linie) stellt den Grenzfall des Planckschen Strahlungsgesetzes (durchgezogene Linie) für hohe Frequenzen (d.h. niedrige Wellenlängen) und niedrige Temperatur, das Rayleigh-Jeanssche (punktierte Linie) den Grenzfall für kleine Frequenzen (d.h. hohe Wellenlängen) und hohe Temperatur dar.