Techniklexikon

piezoelektrischer Effekt

Elektrodynamik und ElektrotechnikFestkörperphysik, Piezoeffekt, Piezoelektrizität, Erzeugung elektrischer Ladungen an der Oberfläche sog. Piezokristalle bei deren Deformation. Er wurde 1880 von Pierre Curie und seinem Bruder Jacques entdeckt.

Piezokristalle sind Kristalle mit polaren Achsen, jedoch ohne Symmetriezentrum. Hierzu gehören a-Quarz, Flüssigkristalle, Turmalin, Seignette-Salz, Zinksulfid und Rohrzucker. Von den 32 Kristallklassen erlauben 20 prinzipiell Piezoelektrizität (polare Symmetrie).

Der umgekehrte Effekt, die Verformung eines gesamten piezoelektrischen Kristalls auf Grund eines äusserlich angelegten elektrischen Feldes, die Elektrostriktion, wird manchmal auch inverser Piezoeffekt genannt.

Der Piezoeffekt kann durch eine Verschiebung der positiven und negativen Ladungen bei Druckausübung erklärt werden, wodurch ein elektrisches Dipolmoment entsteht:

Bringt man einen Isolator mit einer polaren Achse, also einem makroskopischen Dipolmoment, wie z.B. Flüssigkristalle in ein elektrisches Feld, dann verschieben sich die Ladungen darin und die Folge ist eine mechanische Deformation, im Falle von Flüssigkristallen eine Orientierungsdeformation. Umgekehrt kann eine mechanische Deformation - oder im Falle von Flüssigkeiten mechanischer Druck - die Ladungen so verschieben bzw. orientieren, dass eine elektrische Polarisation, also ein elektrisches Feld entsteht. Das Piezofeld E wie auch die zwischen den Stirnflächen erzeugte Spannung U sind proportional zur relativen Deformation e = Dx / x:

d heisst piezoelektrischer Koeffizient und ist für die Hauptachsen eines anisotropen Materials oft sehr verschieden. Die Deformation beruht darauf, dass die in der Feldrichtung hintereinander liegenden Dipole einander anziehen. Benachbarte Schichten werden durch diese Kräfte so lange genähert, bis elastische Gegenkräfte die elektrischen kompensieren.

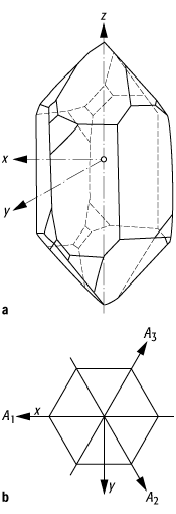
Beim Beispiel des a-Quarzes sind drei polare Achsen vorhanden, welche die jeweils gegenüberliegenden Kanten der sechsseitigen Säule miteinander verbinden (siehe Abb. 1). Die Ladungen treten an den Enden der polaren Achsen auf und werden durch Deformation in deren Ebene gegeneinander verschoben, so dass an der Grenzfläche des insgesamt neutralen Kristalls Oberflächenladungen entstehen (siehe Abb. 2). Der Kristall erfährt also durch die Deformation eine elektrische Polarisation ganz analog zur Polarisation der Dielektrika im elektrischen Feld. Das auftretende elektrische Moment ist dabei der Deformation proportional, was u.a. in Drucksensoren, Mikrophonen und Tonabnehmern in Plattenspielern ausgenutzt wird.

Neuartige synthetische Polymere wie das Polyvinylflourid (PVF₂) sind bis zu fünfmal stärker piezoelektrisch als kristalliner Quarz. Da es sich dabei um ein elastisches Material handelt, ist es als gedehnte PVF₂-Folie leicht als Ultraschallwandler zu verwenden.

Eine weitere neue Anwendung des Pieszoeffekts ergibt sich bei der Erzeugung mechanischer Oberflächenwellen, welche in Festkörpern 100 000mal langsamer sind als elektromagnetische Wellen und daher als Steuer- und Verzögerungsglieder in elektrischen Schaltungen eingesetzt werden. Schliesslich kann man mit piezoelektrischen Kristallen mechanische Verschiebungen bis zu 10^-11 m gezielt und reproduzierbar durchführen, was beispielsweise bei der Rastertunnelmikroskopie von grosser Bedeutung ist.

Effekt">

piezoelektrischer Effekt 1: a) Geometrie eines a-Quarz-Einkristalls: Die z-Achse ist keine Symmetrieachse; b) Kristallquerschnitt senkrecht zur z-Achse mit den drei polaren Achsen A₁, A₂ und A₃.

Effekt">

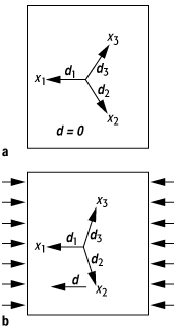
piezoelektrischer Effekt 2: Erzeugung einer piezoelektrischen Verschiebung durch mechanischen Druck: a) Gleichgewichtslage: d = d₁ + d₂ + d₃ =0; b) Kompression: d ¹ 0.