d-Funktion

Petra Nordinghaus-Martin
Mathematische Methoden und Computereinsatzd-Funktion, Diracsche d-Funktion, d-Distribution ein Ausdruck der Form d(x - x0), der eine auf den Punkt x = x0 konzentrierte Verteilung repräsentiert. Mathematisch gesehen handelt es sich bei der d-Funktion um eine Distribution.
bottom:14.15pt;
margin-left:0cm;text-align:justify;background:silver;mso-shading:windowtext;
mso-pattern:solid silver;border:none;mso-border-top-alt:.75pt;mso-border-left-alt:
.75pt;mso-border-bottom-alt:1.5pt;mso-border-right-alt:1.5pt;mso-border-color-alt:
black;mso-border-style-alt:solid;padding:0cm;mso-padding-alt:2.0pt 2.0pt 2.0pt 2.0pt\'>"Um
ein Bild von d(x)
zu bekommen, betrachte man eine Funktion der reellen Variablen x, die überall
verschwindet ausser in einem kleinen Bereich, angenommen der Länge e,
um den Ursprung x = 0 und die innerhalb des Bereichs so gross ist, dass ihr
Integral über diesem Bereich gleich 1 ist. Wie die Funktion innerhalb des
Bereiches genau aussieht, ist unwesentlich, vorausgesetzt sie nimmt keine
unnötig unsinnigen Formen an (wäre zum Beispiel immer von der Ordnung e
-
1). Dann geht diese Funktion für e![]() 0
in die Funktion d(x) über." (Aus: P.A.M. Dirac, "The Principles
of Quantum Mechanics", 4. Auflage, Oxford 1958, S. 58.)
0
in die Funktion d(x) über." (Aus: P.A.M. Dirac, "The Principles
of Quantum Mechanics", 4. Auflage, Oxford 1958, S. 58.)
Der Gebrauch der d-Funktion lässt sich bis auf Kirchhoff
1882 zurückverfolgen, wird jedoch meist mit Dirac in Verbindung
gebracht, der sie in die Quantenmechanik einführte. Man stellt sich die d-Funktion
zweckmässigerweise als unendlich hohe und unendlich schmale Spitze vor, deren
Fläche 1 ist. Die für das praktische Rechnen wichtigste Eigenschaft der d-Funktion
ist, dass sie unter einem Integral einer beliebigen "vernünftigen"
Funktion deren Funktionswert an einer Stelle zuweist:![]() .
.
Diese sowie einige weitere Rechenregeln und Formeln sind in Tabelle 1 zusammengestellt.
Mit Hilfe der d-Funktion lässt sich das Teilchenbild in die
Feldtheorie übernehmen: Eine Punktladung der Stärke q im Punkt r0
besitzt die Ladungsverteilung r(r) = qd(r - r0). Das Potential einer
solchen Punktladung ergibt sich als Lösung der Poisson-Gleichung ![]() zu
zu
![]() .
.
Eine weitere wichtige Anwendung ist die Beschreibung von instantanen Impulsüberträgen: Eine Kraft, die nur in einem kleinen Zeitraum um t = t0 wirkt und insgesamt einen Impulsübertrag von p verursacht, kann durch F(t) = pd(t - t0) beschrieben werden, wenn zwar der Impulsübertrag, aber nicht der genaue Kraftverlauf physikalisch relevant ist.
In der Statistik ermöglicht die d-Funktion die Vereinheitlichung diskreter und stetiger Zufallsgrössen: Eine Zufallsgrösse, die mit gleicher Wahrscheinlichkeit die Werte 0 und 1 annimmt, kann beispielsweise durch die Wahrscheinlichkeitsdichte f(x) = 1/2 (d(x - 0) + d(x - 1)) beschrieben werden.
In der Quantenmechanik sind d-Funktionen in der Ortsdarstellung die Eigenfunktionen des Ortsoperators: Führt man an einem Elektron, das durch die Wellenfunktion y beschrieben wird, eine Ortsmessung durch, bei der man das Resultat r0 erhält, dann ist die Wellenfunktion des Elektrons nach der Messung y = d(r - r0). Die Eigenfunktionen des Impulsoperators, die ebenen Wellen, besitzen im Impulsraum ebenfalls die Form von d-Funktionen. Somit sind über den Gebrauch der d-Funktion Wellen- und Teilchenbild in die Quantenmechanik eingebettet.
Ausser diesen unmittelbar physikalischen Bedeutungen spielt die d-Funktion noch bei der Lösung von Differentialgleichungen mit der Methode der Greenschen Funktionen und als Kriterium für die Vollständigkeit von Funktionensystemen eine Rolle.
Die d-Funktion ist zwar ein nützliches Objekt, aber
sie ist keine Funktion im Sinne einer eindeutigen Abbildung x ![]() d(x). Für einen strengen
mathematischen Zugang zur d-Funktion kann man einen der beiden folgenden
Wege beschreiten, von denen der erste mächtiger und der zweite intuitiver ist:
d(x). Für einen strengen
mathematischen Zugang zur d-Funktion kann man einen der beiden folgenden
Wege beschreiten, von denen der erste mächtiger und der zweite intuitiver ist:
a) Man betrachtet anstelle der d-Funktion d(x
-
x0) die
sogenannte d-Distribution
dx0, d.h. das
Funktional, das jeder Funktion f(x) ihren Funktionswert an der Stelle x0 zuweist (dx0[f]: f(x) ![]() f(x0)), und identifiziert die Integration über die d-Funktion
mit der d-Distribution:
f(x0)), und identifiziert die Integration über die d-Funktion
mit der d-Distribution:
![]() . Bei dieser
Herangehensweise hat die d-Funktion nur dann eine wohldefinierte
Bedeutung, wenn sie unter einem Integral steht.
. Bei dieser
Herangehensweise hat die d-Funktion nur dann eine wohldefinierte
Bedeutung, wenn sie unter einem Integral steht.
b) Man fasst die d-Funktion formal als
"Grenzfunktion" einer Folge von Funktionen dn auf, die mit
zunehmendem n immer schmaler und spitzer werden, wobei ihre Fläche
gleich bleibt. Tabelle 2 enthält einige Funktionenfolgen, die hierfür verwendet
werden können. Bei der Integration über die d-Funktion ist dann
derart vorzugehen, dass zuerst (Riemann-)integriert und danach der Grenzwert
gebildet wird: ![]() . In diesem Fall
dürfen Integration und Grenzwertbildung nicht vertauscht werden; die
Operationen in anderer Reihenfolge durchzuführen, würde keinen Sinn ergeben, da
die Folge der dn
nicht im üblichen Sinne konvergiert. [GB1]
. In diesem Fall
dürfen Integration und Grenzwertbildung nicht vertauscht werden; die
Operationen in anderer Reihenfolge durchzuführen, würde keinen Sinn ergeben, da
die Folge der dn
nicht im üblichen Sinne konvergiert. [GB1]
bottom:14.15pt;margin-left:0cm;text-align:center;background:silver; mso-shading:windowtext;mso-pattern:solid silver;border:none;mso-border-top-alt: .75pt;mso-border-left-alt:.75pt;mso-border-bottom-alt:1.5pt;mso-border-right-alt: 1.5pt;mso-border-color-alt:black;mso-border-style-alt:solid;padding:0cm; mso-padding-alt:2.0pt 2.0pt 2.0pt 2.0pt\'>d-Funktion 1: Einige Rechenregeln und Formeln im Zusammenhang mit der d-Funktion.
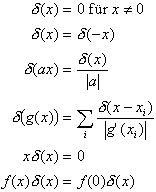

bottom:14.15pt;margin-left:0cm;text-align:center;background:silver;
mso-shading:windowtext;mso-pattern:solid silver;border:none;mso-border-top-alt:
.75pt;mso-border-left-alt:.75pt;mso-border-bottom-alt:1.5pt;mso-border-right-alt:
1.5pt;mso-border-color-alt:black;mso-border-style-alt:solid;padding:0cm;
mso-padding-alt:2.0pt 2.0pt 2.0pt 2.0pt\'>d-Funktion 2: Einige
Funktionenfolgen, als deren Limes für n ![]() ¥ die d-Funktion angesehen
werden kann.
¥ die d-Funktion angesehen
werden kann.
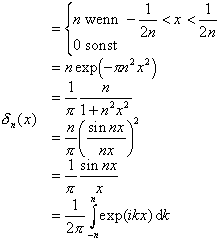
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.