Techniklexikon

Vierervektor

Relativitätstheorie und GravitationMathematische Methoden und Computereinsatz, Weltvektor, Vektor in der vierdimensionalen relativistischen Raumzeit. Man unterscheidet kontravariante und kovariante Vierervektoren. Erstere transformieren sich unter Koordinatenwechsel wie der infinitesimale Ereignisvektor , also gemäss

kovariante Vierervektoren  hingegen wie der Gradient einer Koordinateninvarianten,

Die Transformationskoeffizienten  berechnen sich aus den Transformationsgleichungen der Koordinaten. Bei einer Transformation von einem Inertialsystem in ein anderes etwa sind sie durch die Lorentz-Transformationen  gegeben, d.h.

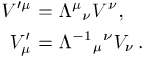
Kovariante und kontravariante Vektoren können durch Multiplikation mit der Metrik ineinander umgewandelt werden. Summen von Vierervektoren gleichen Typs sind wieder Vierervektoren desselben Typs, Produkte von Vierervektoren sind Tensoren. Liegen Vierervektoren innerhalb des Lichtkegels, so heissen sie zeitartig. Ein Beispiel hierfür ist der Tangentenvektor an die Weltlinie eines massebehafteten Teilchens in der vierdimensionalen Raumzeit. Liegen sie auf dem Lichtkegel, so heissen sie lichtartig, und liegen sie ausserhalb desselben, so heissen sie raumartig.

Wichtige relativistische Vierervektoren sind die Vierergeschwindigkeit  eines Teilchens (: Eigenzeit), der Viererimpuls  (: Ruhemasse des Teilchens), die Lorentz-Viererkraftdichte, die Viererstromdichte  oder das Viererpotential . In Analogie zu den dreidimensionalen Differentialoperatoren, die mit Hilfe des Nabla-Operators  gebildet werden, erhält man die vierdimensionalen, Lorentz-invarianten Differentialoperatoren, die mit  die folgende Gestalt annehmen: Gradientenoperator , Divergenz  und vierdimensionaler Laplace-Operator bzw. Quabla-Operator .

Der Nutzen der Verwendung von Vierervektoren in der Relativitätstheorie ergibt sich zum einen daraus, dass Vierervektorgleichungen (allgemein: Tensorgleichungen), die in einem bestimmten Koordinatensystem gelten, dann automatisch in allen Koordinatensystemen gültig sind. Zum anderen ergeben sich aus der Konstruktion von Vierervektoren neue Zusammenhänge. So entpuppt sich beispielsweise die nullte Komponente des Viererimpulses als die Energie dividiert durch die Lichtgeschwindigkeit c, und somit schliesst die Erhaltung des Viererimpulses auch die Erhaltung der Energie ein.