Techniklexikon

Sperrwandler

Elektronik, Halbleiterphysik, ein Gleichspannungswandler (Schaltregler), bei dem nur in der Sperrphase eines Schalttransistors ein Strom durch den Lastwiderstand fliesst. Er besteht aus einem Schalttransistor, einer Diode und einer Induktivität und einem Kondensator als Tiefpass zur Mittelwertsbildung. In der Leitphase wird die Induktivität aufgeladen und in der Sperrphase über den Lastwiderstand entladen. Unter der Annahme, dass der Strom durch die Induktivität nicht Null wird, ist die Ausgangsspannung U_a durch  gegeben (U_e: Eingangsspannung, t_aus: Dauer der Sperrphase, T: Schaltperiodendauer). Es ist daher .

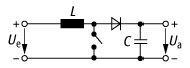
Sperrwandler: Schaltbild (U_e: Eingangsspannung, U_a: Ausgangsspannung, L: Induktivität, C: Kapazität).

spezielle FunktionenMathematische Methoden und Computereinsatz, höhere transzendente Funktionen der mathematischen Physik, die vornehmlich zwischen 1700 und 1960, also vor der grösseren Verbreitung leistungsstarker Computer, entwickelt wurden. Das wohl umfangreichste und vollständigste Werk über spezielle Funktionen ist das Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables von M. Abramowitz und C.A. Stegun. Nachdem für spezielle Funktionen effiziente Methoden, z.B. schnell konvergente Reihen oder Kettenbruchentwicklungen, zur Verfügung standen, verbreiteten sich diese spezielle Funktionen rapide, und die Lösungen physikalischer oder technischer Fragestellungen wurden mit ihrer Hilfe formuliert. Die Verfügbarkeit leistungsstarker Computer mindert die Bedeutung der speziellen Funktionen nur bedingt, denn diese Funktionen sind gut tabelliert und helfen, eigene Computerprogramme und Algorithmen zu testen. Viele der speziellen Funktionen mit oft mehreren Parametern sind exakte Lösungen der Differentialgleichungen der theoretischen Physik. Hierzu zählen die elliptischen Integrale als Referenzintegrale zur Auswertung von Integralen mit rationalen Integranden, die elliptischen Funktionen zur Auswertung von Differentialgleichungen in der klassischen Mechanik, die Familie der Bessel-Funktionen zur Lösungen der Bessel-Gleichung, die sphärische Bessel-Funktion, die Kugelfunktionen zur Lösung von Differentialgleichungen, die bei Verwendung von sphärischen Polarkoordinaten (Kugelkoordinaten) die Separation der Variablen zulassen, die konfluenten hypergeometrischen Funktionen als Lösung der Laplaceschen bzw. konfluenten, hypergeometrischen Differentialgleichungen, die Coulomb-Funktionen als partikuläre Lösungen der Radialgleichung des Streuproblems (Teilchen an reinem Coulomb-Potential), die parabolischen Zylinderfunktionen als Lösung der Differentialgleichung  oder die Mathieu-Funktionen als Lösung der Differentialgleichung . Zu den speziellen Funktionen zählen aber auch Funktionen aus Kombinatorik und Statistik wie die G-Funktion , die Beta-Funktion , Fakultäten, Binomialkoeffizienten, die unvollständige G-Funktion  für  die unvollständige Beta-Funktion , Poisson-Verteilung und Normalverteilung, kumulative Poisson- und Normalverteilung, die Gausssche Fehlerfunktion , die Fresnel-Integrale  und , Integralfunktionen wie

mit der Eulersche Konstante , oder das Dawson-Integral .