Techniklexikon

Wightman-Axiome

Quantenmechanik, in den 50er Jahren von A.S.Wightman formuliertes Axiomensystem für die Vakuumerwartungswerte (Wightman-Funktionen) einer relativistischen Quantenfeldtheorie (axiomatische Quantenfeldtheorie). Erfüllt ein Satz von Distributionen die Wightman-Axiome, so lassen sich die relativistischen Quantenfeldoperatoren rekonstruieren, deren Vakuumerwartungswerte diesen Distributionen entsprechen (Theorem von Streater und Wightman). Die Wightman-Axiome lassen sich auch äquivalent als Eigenschaften der Feldoperatoren formulieren.

Zu Erläuterung der Axiome (der Einfachheit halber für ein skalares Feld) definieren wir zu einer Wightman-Distribution  (wobei x_i Punkte im Minkowski-Raum sind) und einer geeigneten Testfunktion  über dem  die Verschmierung:

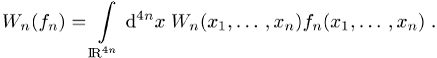
Die Axiome im einzelnen sind:

1. Temperiertheit: Die Wightman-Distributionen sind temperierte Distributionen.

2. Relativistische Invarianz: Die Wightman-Distributionen sind invariant unter Poincaré-Transformationen:

mit

für eine Lorentz-Transformation L und einen Vektor . Handelt es sich um die Vakuumerwartungswerte einer nicht-skalaren relativistischen Feldtheorie, so transformieren sich die Wightman-Distributionen nach der entsprechenden Darstellung der Felder.

3. Spektralbedingung: Die Fourier-Transformierten (Fourier-Transformation) der Wightman-Distributionen verschwinden für Energie-Impuls-Vektoren, die nicht innerhalb oder auf dem positiven Lichtkegel (, ) liegen. Diese Bedingung garantiert, dass das Spektrum des Energie-Impuls-Tensors nur physikalische Werte annimmt.

4. Hermitizität: Es gilt

Bei mehrkomponentigen (komplexen) Feldern ist die rechte Seite durch die Wightman-Distribution zu den adjungierten Feldern zu ersetzen.

5. Lokale Kommutativität (Mikrokausalität):

falls  raumartig ist. Für fermionische Felder ergibt die Vertauschung raumartiger Argumente noch einen Faktor (-1).

6. Positivität: Für endliche Folgen von Testfunktionen {f_n} gilt:

Diese Bedingung bedeutet, dass die Norm von Zuständen nicht-negativ ist und erlaubt so die Rekonstruktion eines positiv-definiten Skalarprodukts auf dem Hilbert-Raum der Quantenfelder.

7. Cluster-Bedingung: Für einen raumartigen Vektor a gilt:

Diese Forderung garantiert die Eindeutigkeit des Vakuumzustands.