Techniklexikon

Dissipations-Fluktuations-Theorem

Thermodynamik und statistische Physik, Dissipations-Schwankungs-Theorem, Fluktuations-Dissipations-Theorem, von H.B. Celton und T.A. Welton 1951 gefundener allgemeiner Zusammenhang zwischen der linearen Reaktion eines Gleichgewichtssystems auf schwache äussere Störungen (lineare Antwort, linear response) und den zeitlichen Korrelationen von Gleichgewichtsschwankungen oder Schwankungserscheinungen.

Das Dissipations-Fluktuations-Theorem bildet eine Brücke zwischen Gleichgewichts- und Nichtgleichgewichtsstatistik. Dem Theorem liegt der physikalische Sachverhalt zugrunde, dass die Reaktion des Systems auf Abweichungen gegenüber den statistischen Mittelwerten nicht davon abhängt, ob diese Abweichungen durch zufällige Fluktuationen oder durch äussere Einwirkung entstanden sind. Im einfachsten Fall koppelt die äussere Einwirkung an eine einzige skalare physikalische Grösse A des Systems; die Hamilton-Funktion bzw. der Hamilton-Operator des gestörten Systems lautet dann H = H⁰ - AX(t), wobei X(t) als beliebig vorgebbare verallgemeinerte Kraft aufzufassen ist. Die Reaktion des Systems wird durch eine verallgemeinerte, komplexe und frequenzabhängige Suszeptibilität a(w) entsprechend  beschrieben. Die Autokorrelationsfunktion der Gleichgewichtsschwankungen kann bei einem quantenmechanischen System durch Benutzung des Antikommutators  als reelle Funktion definiert werden;  ist der Operator in Heisenberg-Darstellung; die spitzen Klammern bezeichnen den quantenstatistischen Mittelwert; vereinfachend wurde der ungestörte Mittelwert  selbst gleich null gesetzt. Aus der gegebenen Definition folgt f(t) = f( - t).

Das Dissipations-Fluktuations-Theorem verknüpft die Fourier-Transformierte von f(t) mit dem Imaginärteil der komplexen Suszeptibilität:

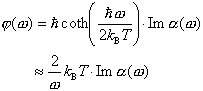
k_B ist die Boltzmann-Konstante und T die Temperatur.  kann als mittlere Energie eines harmonischen Oszillators im Gleichgewicht aufgefasst werden, entsprechend ist k_BT der klassische Grenzwert dieser Grösse. Die Bedeutung von f als Fluktuationsgrösse ist offensichtlich, und Im a bestimmt die Energiedissipation bei äusserer Störung, d.h. die Verteilung der über die äussere Kraft am System verrichteten Arbeit auf die vielen mikroskopischen Freiheitsgrade des Systems (Dissipation). (Unter isothermen Bedingungen wird die dissipative Energie durch Wärmeleitung schliesslich an den umgebenden Thermostaten abgegeben.) Das bekannteste Beispiel ist der Imaginärteil der verallgemeinerten komplexen Dielektrizitätskonstanten e*, die proportional zum Realteil der Leitfähigkeit ist.

Das Dissipations-Fluktuations-Theorem kann einerseits benutzt werden, um aus Aussagen oder Näherungen für die Suszeptibilität entsprechende Aussagen über f(t) zu gewinnen. Das gilt insbesondere für die Ermittlung des Schwankungsquadrats . Auf diese Weise können die Dichteschwankungen und die damit unmittelbar zusammenhängende Paarverteilungsfunktion aus der linearen Antwort auf ein äusseres Störungspotential ermittelt werden. Vorherrschend ist aber die Anwendung des Theorems zur Ermittlung von Transportkoeffizienten; insbesondere kann die Leitfähigkeit auf das Verhalten langwelliger Stromfluktuationen zurückgeführt werden.

Falls mehrere physikalische Grössen A_i und zugeordnete Kräfte X_i(t) gleichzeitig betrachtet werden, also , besitzt die Matrix der gemischten Korrelationsfunktionen Symmetrieeigenschaften, die aus der (eventuell durch ein äusseres Magnetfeld modifizierten) mikroskopischen Reversibitität folgen. Daraus ergeben sich entsprechende Symmetrieeigenschaften der Transportkoeffizienten, insbesondere die Onsager-Casimirschen Reziprozitätsbeziehungen in der Thermodynamik irreversibler Prozesse. Diese Relationen haben im Dissipations-Fluktuations-Theorem ihre theoretische Wurzel. [JS2]