Techniklexikon

Glashow-Weinberg-Salam-Modell

Teilchenphysik, GWS-Modell, nichtabelsche Eichtheorie (Yang-Mills-Theorie) der elektroschwachen Wechselwirkung, die von S.L. Glashow, S. Weinberg und A. Salam in den sechziger Jahren entwickelt wurde. Das Modell basiert auf der elektromagnetische und schwache Kraft vereinigenden Eichgruppe SU(2) ´ U(1) mit zunächst masselosen Eichbosonen, die ihre erforderliche Masse durch die spontane Symmetriebrechung erhalten. Seit der Theorie von Fermi (Fermi-Theorie) hatten eine Reihe von Arbeiten die Existenz eines massiven Vektorbosons als Träger der schwachen Wechselwirkung postuliert und entsprechende Theorien formuliert, die jedoch nur als phänomenologische Beschreibung und nicht als fundamentale Theorie betrachtet wurden, da sie sich als nicht renormierbar erwiesen. 1971 zeigte G. t\'Hooft jedoch, dass Yang-Mills-Theorien auch dann, wenn ihre Symmetrie spontan gebrochen ist, renormierbar sind. Eichtheorien konnten nun also konkrete und experimentell überprüfbare numerische Vorhersagen machen und wurden daher untereinander vergleichbar. Das GWS-Modell setzte sich dabei gegen konkurrierende Theorien durch: seine Übereinstimmung mit dem Experiment, die einen Höhepunkt in der Entdeckung der vorhergesagten W- und Z-Bosonen 1983 hatte, wurde in den letzten Jahrzehnten immer präziser bestätigt. Das GWS-Modell bildet zusammen mit der Eichtheorie der starken Wechselwirkung, der Quantenchromodynamik, das moderne Standardmodell der Elementarteilchen. Streng gesprochen handelt es sich beim GWS-Modell nicht um eine vereinigte Feldtheorie, da für jede der beiden Wechselwirkungen eine eigene Kopplungskonstante eingeführt werden muss.

Der SU(2)-Sektor des GWS-Modells besteht in jeder Generation als Konsequenz der paritätsverletzenden (V-A)-Struktur der schwachen Wechselwirkung aus einem Isodublett der linkshändigen Leptonen, dem Elektron und seinem Neutrino:  sowie dem rechtshändigen Elektron, einem Isosingulett: .

Zur Eichgruppe SU(2) gehören weiterhin drei Eichbosonen  (i = 1,2,3), zur U(1) eines: B_m. Die entsprechenden Kopplungskonstanten sind g und g¢. Schliesslich besitzt das GWS-Modell noch ein Higgs-Dublett , dessen Erwartungswert  die Symmetriebrechung der Theorie induziert.

Durch die Symmetriebrechung rekombinieren die Eichfelder B_m und W_m zum masselosen Photonfeld , einem neutralen massiven Vektorfeld  sowie einem massiven, geladenen Dublett . Die Mischung der Kopplungskonstanten wird durch den Weinberg-Winkel q_W = tan^-1(g¢ / g) parametrisiert. Die Massen der neuen Vektorteilchen lassen sich aus dem Massenterm ablesen, den die Symmetriebrechung aus dem Higgs-Sektor der ursprünglichen Lagrange-Dichte erzeugt:  =  = gv / 2 und . Der Weinberg-Winkel fixiert also das Verhältnis der Vektorteilchenmassen, cosq_W = M_W / M_Z; diese Beziehung ist durch die aktuellen experimentellen Werte der drei Parameter sin²q_W = 0,23124(24), M_W = 80,405(89) GeV / c² und M_Z = 91,1867(20) GeV / c² hervorragend erfüllt.

Die Einbeziehung der anderen Leptonpaare (n_m, m^-) und (n_t, t^-) in das GWS-Modell geschieht einfach dadurch, dass man zur bisherigen Lagrange-Dichte entsprechende, in der Struktur völlig identische Terme addiert. Auch die Ausdehnung auf Quarks ist problemlos: analog zu den Leptonen bildet man die linkshändigen SU(2)-Dubletts , , , wobei die Quark-Mischungen  durch die Cabibbo-Kobayashi-Maskawa-Matrix (CKM-Matrix) V generiert werden.

Neben der Entdeckung der Vektorbosonen W^± und Z gehören Vorhersage und Nachweis der neutralen schwachen Wechselwirkung zu den wichtigen Tests des GWS-Modells. Der Nachweis gelang 1973 durch die Beobachtung von Prozessen des Typs n + N  n + Hadronen, wobei im Endzustand kein Myon zu beobachten ist. Solchen Reaktionen liegt der Austausch neutraler Z-Bosonen zugrunde. Da auch die elektromagnetische Wechselwirkung neutrale Prozesse durch Photonaustausch ermöglicht, gibt es interessante Interferenzphänomene zwischen elektromagnetischer und schwacher Wechselwirkung, die von kleinen paritätsverletzenden Effekten begleitet sind. Einige raffinierte Experimente konnten auch diese Vorhersage bestätigen. Das GWS-Modell stellt somit einen der QED ebenbürtigen Erfolg in der Quantenfeldtheorie dar und wird zu Recht als elektroschwaches Standardmodell bezeichnet. [UK]

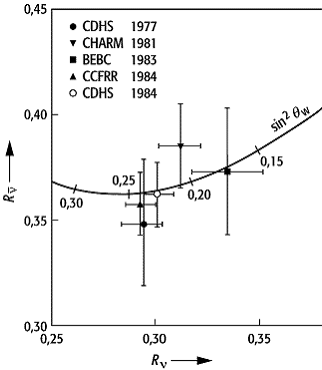
Glashow-Weinberg-Salam-Modell: Bestimmung des Weinbergwinkels q_W aus verschiedenen Messungen des Verhältnisses R von neutralen zu gelandenen Strömen bei Antineutrino- () und Neutrinostreuung (n).