Techniklexikon

Eichtheorie

Relativitätstheorie und Gravitation^[n], allgemeines Modell für eine Feldtheorie, das auf der Forderung nach Invarianz gegenüber lokalen Phasentransformationen aufbaut. Diese lokale Symmetrie hat sich als Grundbaustein für die Beschreibung der fundamentalen Wechselwirkungen von Elementarteilchen erwiesen, da die Raum-Zeit-Abhängigkeit der Transformationen die Existenz unabhängiger Vektorfelder verlangt, die in der physikalischen Natur den Eichbosonen entsprechen, welche die Wechselwirkungen der Teilchen übertragen.

Das grundlegende Konzept der Eichtheorie wurde 1918 von H. Weyl bei dem Versuch der Vereinheitlichung von Gravitation und Elektromagnetismus entwickelt, in der die vereinheitlichte Lagrange-Dichte invariant unter Rekalibrierung ("Eichung") der Längenskala ist. Zwar erwies sich Weyls Theorie als nicht gangbar, sie führte aber in der Folge zur Formulierung der Elektrodynamik als Eichtheorie und schliesslich zum vereinheitlichten Standardmodell der Elementarteilchen als Prototyp einer Yang-Mills-Theorie.

1) Quantenfeldtheorie: Aus quantenfeldtheoretischer Sicht ist die Forderung nach lokaler Eichinvarianz zwingend: Die Quantenmechanik lehrt, dass nur Wahrscheinlichkeitsdichten, nicht jedoch Phasenfaktoren beobachtbar sind, und das Kausalitätsprinzip verbietet die gleichzeitige, nicht-lokale Festlegung der Phasen im ganzen Universum, da dies eine instantane Informationsübertragung voraussetzen würde. Sowohl die elektromagnetische als auch die schwache und die starke Wechselwirkung werden heute als Eichtheorien formuliert. Die Gravitationtheorie lässt sich ebenfalls aus einer Eichsymmetrie gewinnen, allerdings nur auf klassischem Niveau und nicht - wie im Fall der anderen drei Wechselwirkungen - als Quantenfeldtheorie (siehe unten).

Der Mechanismus einer Eichtheorie lässt sich am Beispiel der elektromagnetischen Kraft erläutern: die Dirac-Gleichung  ist nicht invariant unter der lokalen abelschen U(1)-Phasentransformation

des Elektronfeldes y(x); der von der Raum-Zeit-Koordinate abhängige Transformationsparameter a(x) verursacht durch die Ableitung in der Dirac-Gleichung einen zusätzlichen Term, der die Symmetrie zerstört. Erst die Ankopplung des Elektrons an ein Eichfeld A^m, das elektromagnetische Potential, durch die Definition einer verallgemeinerten kovarianten Ableitung  stellt die Symmetrie unter lokalen Phasentransformationen wieder her, wenn gleichzeitig das Vektorfeld entsprechend eichtransformiert wird, ; dadurch wird der störende Term eliminiert. Die Invarianzforderung stellt also ein dynamisches Prinzip dar, das die Ankopplung des Eichfeldes an das Elektronfeld erzwingt. Die elektromagnetische Wechselwirkung lässt sich somit durch eine abelsche Eichtheorie mit der inneren Symmetrie U(1) beschreiben, der Quantenelektrodynamik. Dem Eichfeld entspricht in der Natur das masselose Photon.

Das Eichprinzip kann auf höhere und nicht-abelsche Eichgruppen SU(N) erweitert werden. Bereits 1954 präsentierten C.N. Yang und R.L. Mills eine lokale Version der SU(2)-Eichsymmetrie zur Beschreibung stark wechselwirkender Hadronen. In der Folge hat sich für alle SU(N)-Eichtheorien die Bezeichnung Yang-Mills-Theorien eingebürgert; in ihnen lauten die lokalen Phasentransformationen der fermionischen Felder (in einer bestimmten gewählten Darstellung)

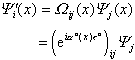
mit den lokalen Variablen a^a(x) und den Erzeugenden t^a der Gruppe mit den charakteristischen Vertauschungsrelationen  (Eichgruppe). Analog zur U(1)-Eichtheorie löst die verallgemeinerte Ableitung  das Problem des störenden Ableitungsterms, denn D_m verhält sich kovariant unter Phasentransformationen, , wenn die Eichfelder (auch Zusammenhang genannt), deren Anzahl der Zahl der Gruppenparameter entspricht, wie  variieren. Aus der Kovarianz der Ableitung D_m folgt automatisch die Kovarianz des Feldstärketensors

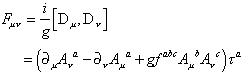
d.h. F_mn transformiert wie . Damit ergibt sich für die Wirkung der Yang-Mills-Theorie als einfachste Möglichkeit

;

sie bildet den Ausgangspunkt für die Quantisierung und die weitere Diskussionen der Eichtheorien.

Der Pfadintegral-Formalismus ermöglicht eine kovariante Quantisierung, für die allerdings die Eichung fixiert werden muss, da alle durch eine Eichtransformation auseinander hervorgehenden Yang-Mills-Theorien physikalisch äquivalent sind (Eichfixierung). Diese Massnahme zerstört jedoch die Unitarität, welche durch die Einführung zusätzlicher skalarer, fermionischer Felder repariert werden muss (Geisterfelder). Die Yang-Mills-Theorie mit der Eichgruppe SU(2) ´ U(1) und insgesamt vier Eichbosonen hat sich, nachdem die Quarks als fundamentale Teilchen etabliert waren und das Problem der Vereinbarkeit von massiven Eichbosonen und Renormierung gelöst war (spontane Symmetriebrechung), erfolgreich als die Theorie der elektroschwachen Wechselwirkung erwiesen (Glashow-Weinberg-Salam-Modell). Ihre geladenen Eichbosonen, die W-Bosonen, wurden 1983 am CERN in -Kollisionen nachgewiesen (Vektorbosonen). Die Eichtheorie der starken Wechselwirkung basiert auf der Eichgruppe SU(3) und erfordert acht Eichbosonen, die Gluonen (Quantenchromodynamik). Im Unterschied zur abelschen U(1)-Eichtheorie tragen die Eichfelder der nicht-abelschen Yang-Mills-Theorien innere Ladungen und können daher miteinander wechselwirken; es existieren also fundamentale Feynman-Diagrammen, die nur Eichfelder enthalten.

Es steht heute ausser Zweifel, dass mit dem Eichprinzip ein wesentlicher Aspekt der Natur aufgedeckt wurde, die Physik aber andererseits erst am Anfang einer interessanten Entwicklung steht, an deren Ende möglicherweise eine vollständige Reduktion physikalischer Begriffsbildungen wie Ladung und Masse auf geometrische Eigenschaften eines universellen hochdimensionalen Raumes stehen könnte.

2)  Gravitation: Die Formulierung der Gravitation als Eichtheorie ist erstens - aufbauend auf dem Erfolg der Beschreibung der starken, der schwachen und der elektromagnetischen Wechselwirkung als Eichtheorie - von der Suche nach einer vereinheitlichten Theorie der vier fundamentalen Wechselwirkungen motiviert und zweitens vom Misserfolg bei der Quantisierung der Allgemeinen Relativitätstheorie (Quantengravitation) angeregt.

Zur Formulierung der Gravitationstheorie als Eichtheorie müssen zunächst sowohl eine Eichgruppe als auch eine eichinvariante Lagrange-Dichte gewählt werden; abhängig von der Wahl ergeben sich verschiedene Modelle. Der allgemeinste Ansatz basiert auf der vierdimensionalen affinen Gruppe , dem semidirekten Produkt der Translationsgruppe  mit der allgemeinen linearen Gruppe . Die Eichung der affinen Gruppe, angelehnt an den Formalismus der Yang-Mills-Eichtheorie, führt zur metrisch-affinen (Eichtheorie der) Gravitation (MAG). Die Eichpotentiale der MAG sind die Metrik g_ab, die Kobasis J^a und die lineare Konnexion G_a^b, die entsprechenden Feldstärken sind die Nichtmetrizität Q_ab, die Torsion T^a und die Krümmung R_ab. Mathematisch ergeben sich die Feldstärken durch Bildung der äusseren kovarianten Ableitung der Eichpotentiale, d.h. formal gilt

.

Die Eichung von Untergruppen der affinen Gruppe führt zu degenerierten Spezialfällen der MAG. Die Poincaré-Eichteorie ist die Klasse von Eichtheorien, die auf der Eichung der Poincaré-Gruppe basieren. Hier ist die Metrik kovariant konstant, d.h. , wodurch sich in Anlehnung an die MAG Torsion und Krümmung als Feldstärken der Poincaré-Eichteorie ergeben. Durch die Festlegung der eichinvarianten Lagrange-Dichte ergeben sich verschiedene Untermodelle, zu denen als wichtigstes Beispiel die Einstein-Cartan-Theorie gehört, die als eine (geringfügige) Verallgemeinerung der Allgemeinen Relativitätstheorie verstanden werden kann. Die experimentellen Vorhersagen der Einstein-Cartan-Theorie weichen nur so schwach von denen der Allgemeinen Relativitätstheorie ab, dass momentan experimentell nicht zwischen den beiden Theorien unterschieden werden kann.

Schliesslich führt die Eichung der Translationsgruppe  zur Fernparallelismus-Theorie der Gravitation, die in den dreissiger Jahren von Einstein selbst formuliert wurde. In dieser Theorie verschwindet ausser der Nichtmetrizität auch die Krümmung, so dass nur die Torsion als gravitative Feldstärke übrigbleibt. Dementsprechend ist die zugrundeliegende Geometrie ein sog. Weitzenböck-Raum. Die Fernparallelismus-Theorie und die Allgemeine Relativitätstheorie sind zwei mathematisch vollständig äquivalente Formulierungen der Gravitation. [BK, TB2, UK]