Techniklexikon

lineare Kette

Klassische Mechanik, einfaches Modell zur Behandlung charakteristischer Eigenschaften der Gitterschwingungen. Der Aufbau eines Kristalls wird dabei vereinfacht dargestellt durch eine eindimensionale Anordnung von Massen, zwischen denen Kräfte wirken. Diese wirken einer Auslenkung aus der Ruhelage entgegen.

Ein Spezialfall der linearen Kette ist die AA-Kette mit gleichen Massen und gleichen Kraftkonstanten. Hier sind  identische Massen  in einem Abstand  durch die Kraftkonstante  miteinander gekoppelt (Abbildung 1). Für die Auslenkungen  der Masse  sollen zyklische Randbedingungen gelten:  mit . Damit beschreibt man Kristalle mit nur einem Atom in der Einheitszelle. Mit der Annahme, dass jeweils nur nächste Nachbarn miteinander wechselwirken, ergibt sich für die Auslenkung  der komplexe Lösungsansatz einer monochromatischen Welle , für deren Frequenz die Dispersionsrelation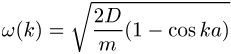

gilt. Ihr Verlauf ist in Abbildung 2 wiedergegeben. Für kleine Wellenzahlen  gilt in erster Näherung . Die Verschiebungen  für die Wellenzahlen  und  ( ganze Zahl) sind identisch, so dass man sich auf die erste Brillouin-Zone mit  beschränken kann. Da aus der Periodizitätsbedingung  folgt, bedeutet dies ausserdem, dass es nur N physikalisch unterscheidbare Wellenzahlen und damit Schwingungsmoden gibt. Für sehr grosse N kann man die Kontinuumsvorstellung verwenden. Die Anzahl der möglichen Wellenzahlen in einem Wellenzahlenbereich  ist dann durch  gegeben. Wenn  die Anzahl der möglichen Schwingungsmoden mit Frequenzen zwischen  und  darstellt, gilt also:

(der Faktor 2 ist nötig, da k zur selben Frequenz  sowohl negativ als auch positiv sein kann). Für die Frequenzverteilung der Schwingungsmoden der linearen Kette erhält man

wobei  die maximal mögliche Frequenz darstellt (Abbildung 3). Es gilt natürlich die Normierung

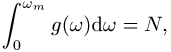
d.h. insgesamt sind N Schwingungsmoden erlaubt.

Die Variante der linearen Kette mit zwei unterschiedlichen Massen (AB-Kette) lässt sich auf Kristalle anwenden, bei denen sich in der Einheitszelle der Länge a zwei Atome mit unterschiedlichen Massen  und  in einem Abstand von  befinden (Abbildung 4). Der Ansatz mit ebenen Wellen führt jetzt auf die Dispersionsrelation

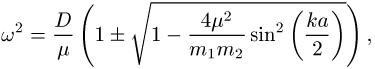
deren Verlauf in Abbildung 5 wiedergegeben ist (: reduzierte Masse). Im Gegensatz zur einatomigen Kette treten hier zwei getrennte Zweige auf. Derjenige, dessen Frequenz bei kleinen Wellenzahlen k nicht verschwindet, heisst optischer Zweig, den anderen, dessen Frequenz proportional zu k verschwindet

, nennt man akustischen Zweig. Das Amplitudenverhältnis der Auslenkungen der schweren und der leichteren Massen  ergibt sich zu

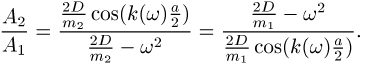
Hieraus folgt, dass die Atome in einer Elementarzelle, insbesondere im Fall langer Wellenlängen, bei den Frequenzen des akustischen Zweiges gleichphasig () und bei den Frequenzen des optischen Zweiges in entgegengesetzter Phase schwingen (). Bei  schwingen im optischen Zweig die beiden Teilgitter starr gegeneinander: ; für  am Rand der ersten Brillouin-Zone ruhen im optischen Zweig die schweren Massen  (), und die leichten Massen  schwingen mit entgegengesetzter Amplitude. Dagegen verharrt im akustischen Zweig das Teilgitter der leichten Massen in Ruhe (), während die benachbarten Atome der schweren Massen im Gegentakt schwingen. Das Gitterschwingungsspektrum einer linearen Kette mit den Massen  zeigt Abbildung 6.Die Berechnung der Dispersionsrelation für Gitterschwingungen in dreidimensionalen Kristallen verläuft vollkommen analog. Man erhält jedoch aufgrund der grösseren Zahl an Freiheitsgraden auch mehr Zweige, nämlich stets drei akustische (zwei transversale und einen longitudinalen) sowie  optische Zweige, wobei s für die Anzahl der Atome in der Einheitszelle steht; für  also  Zweige (Abbildung 7). Bei den longitudinalen Moden schwingen die Massen wie in dieser Betrachtung längs der Kette (Longitudinalwellen), bei den transversalen Moden hingegen quer dazu (Transversalwellen).

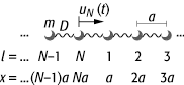
lineare Kette 1: Eine lineare Kette mit identischen Massen m und den Kraftkonstanten D zwischen nächsten Nachbarn. Der Abstand zweier Massen beträgt a.

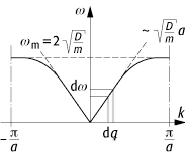
lineare Kette 2: Dispersionsrelation für die lineare Kette mit gleichen Massen. Der Abstand zwischen zwei erlaubten Wellenzahlen k beträgt .

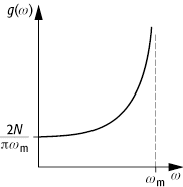
lineare Kette 3: Gitterspektrum einer einatomigen linearen Kette.

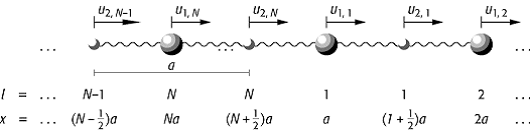
lineare Kette 4: Zweiatomige lineare Kette mit den Massen m₁ und m₂. Die Kraftkonstante zwischen nächsten Nachbarn im Abstand a / 2 beträgt D.

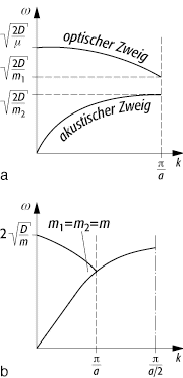
lineare Kette 5: Dispersionsrelation einer zweiatomigen linearen Kette (dargestellt nur für k₀). a) m₁ < m₂. b) m₁ = m₂. Die Brillouin-Zone wurde erweitert, weil die Elementarzelle bei zwei gleichen Massen verkleinert ist. Dieser Fall entspricht der einatomigen linearen Kette.

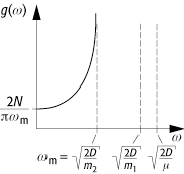
lineare Kette 6: Gitterspektrum einer zweiatomigen linearen Kette mit m₁ < m₂.

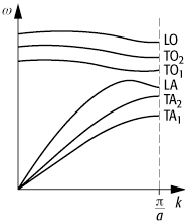
lineare Kette 7: Dispersionsrelation der Gitterschwingungen eines dreidimensionalen anisotropen Gitters mit zwei Atomen pro Einheitszelle. Dargestellt sind jeweils ein longitudinaler (L) und die beiden transversalen (T) Moden für den optischen (O) und den akustischen (A) Zweig.