Techniklexikon

inverse Streutheorie

^[n]Quantenmechanik, Teilgebiet der Streutheorie, das sich mit der Rückgewinnung bzw. Berechnung des Streupotentials aus den Streudaten beschäftigt. Im nichtrelativistischen Fall bilden die aus dem differentiellen Wirkungsquerschnitt gewonnenen Phasenverschiebungen (Streuphasen) d₁(k) zu Partialwellen mit Bahn-Drehimpuls l und Teilchenenergie  die Grundlage der mathematischen Methoden, die die Bestimmung des Potentials V(r) zum Ziel haben. Falls das Potential auch gebundene Zustände zulässt, müssen ausser den Phasenverschiebungen auch die jeweiligen Bindungsenergien bekannt sein. Die Normierung der gebundenen Zustände, , liefert die Vollständigkeitsrelation. Da gebundene Zustände negative Energie haben, ist der zugehörige Impuls k rein imaginär, .

Nach der Gel\'fand-Levitan-Jost-Kohn-Methode sind folgende Rechenschritte erforderlich:

1) Bestimmung der Jost-Funktion aus Phasenverschiebung und Bindungsenergie,

.

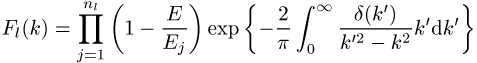2) Konstruktion des Kerns mit Hilfe der freien Wellenfunktion ,

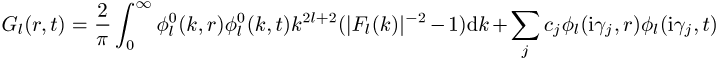
3) Bestimmung der Inversen über die Integral-Gleichung (Gel\'fand-Levitan-Gleichung);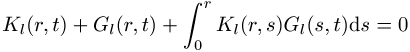

sie erfüllt die radiale Gleichung  mit den Differentialoperatoren der Schrödinger-Gleichung,  (D_t entsprechend).

4) Schliesslich wird das Potential aus dem Kern K rekonstruiert:.

Ob sich für alle l das gleiche Potential V(r) rekonstruieren lässt, d.h. welche Kompatibilitätsbedingungen die Streuphasen erfüllen müssen, ist unbekannt.

Die Marchenko-Methode benutzt eine Transformation der Schrödinger-Gleichung. Die Fourier-Entwicklungskoeffizienten (Fourier-Reihe) der Streuamplitude f(k,r), gegeben durch

,

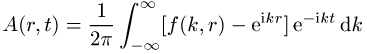sind nur für t < r von Null verschieden und erfüllen die Gleichung

. Deshalb hat das Potential die Form

. Die Amplitude A_l(r,t) ist durch eine Integral-Gleichung bestimmt,

,

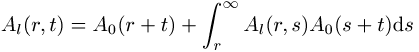wobei die Funktion A₀(t) durch die S-Matrix bestimmt wird:

.

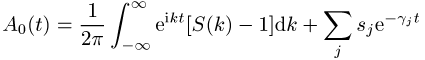Besondere Methoden sind auf die Probleme mit festem l (Krein-Methode) oder festem E (Matrixmethoden, Operatormethoden) anzuwenden. Näherungen, wie Invertierung der Bornschen Reihe, semiklassische Entwicklung usw., und numerische Rechnungen ergänzen das Repertoire. Das Invertierungsproblem der Streuung taucht auch in komplexeren Systemen auf, etwa in der eindimensionalen (nichtradialen) Soliton-Streuung oder in anisotropischen oder relativistischen Streuproblemen in drei Dimensionen.