Techniklexikon

Konformation

Biophysik, Konformer, unterschiedliche Zustände eines Moleküls, die durch verschiedene räumliche Anordnungen der beteiligten Atome charakterisiert sind. Sie entstehen durch Veränderungen der inneren geometrischen Parameter eines Moleküls (innere Koordinaten). Dazu gehören Deformationen der Bindungslängen (Abstände von paarweise chemisch gebundenen Atomen) und der Valenzwinkel (Winkel zwischen zwei chemischen Bindungen eines Atoms zu zwei weiteren Atomen) und Veränderungen der Torsionswinkel, die Drehungen um chemische Bindungen, in der Regel s-Bindungen, beschreiben (Rotationsisomerie). Konformationsübergänge sind nicht mit der Bildung oder der Auflösung chemischer Bindungen verbunden. Wasserstoffperoxid (HOOH) ist das einfachste Molekül, auf welches der Begriff der Konformation angewendet werden kann. Unterschiedliche relative räumliche Lagen der Wasserstoffatome sind das Resultat von Drehungen um die O-O Bindung. Im Zyklohexan entsteht die Konformation der Wanne (siehe Abb. 1) und mögliche andere Lagen der C-Atome aus der energetisch günstigsten Sessel-Konformation durch die Veränderung mehrerer innerer geometrischer Parameter. Das Ammoniakmolekül geht stochastisch aus einer tetraedrischen Konformation in die gespiegelte Lage über (Inversion des Moleküls, siehe Abb. 2). Die ebene Übergangskonformation entsteht durch Deformationen der Valenzwinkel (Energiebarriere 25 J / mol, Spektrallinie des Überganges 400 cm^-1). Kompliziertere innere Koordinaten beschreiben die Konformationen von Metallkomplexen. Im Ferrozän (siehe Abb. 3) drehen sich zwei ebene Zyklopentadienringe um eine Achse durch die Zentren der Ringe und das Metallion beim Übergang von der prismatischen in die antiprismatische Form.

Im typischen Fall unterscheiden sich verschiedene Konformationen durch Drehungen um Einfachbindungen (Rotamere, Rotationsisomerie). Es gibt z.B. drei lokal stabile Rotamere des n-Butan CH₃-CH₂-CH₂-CH₃. Im sogenannten trans-Rotamer, der stabilsten Konformation, ist der Torsionswinkel bei der mittleren Bindung 180^o. Hier ist der Nullpunkt definiert für den Fall, dass alle vier C-Atome in einer Halbebene bezüglich der mittleren Bindung liegen. Die beiden gauche-Konformationen haben einen Winkel von ±60^o.

Die Gesamtheit aller Konformationen K bildet den Konformationsraum W. Wenn man mittlere physikalische Eigenschaften <E> eines Moleküls bestimmen will, muss E(K) über das Ensemble aller Konformationen gemittelt werden. Dazu ist die Angabe der Wahrscheinlichkeitsdichte p(K) des Vorkommens einer Konformation notwendig: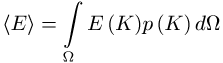

Die Grösse p(K) hängt von der Konformationsenergie U ab, sie ist proportional zu  (k: Boltzmann-Konstante, T: absolute Temperatur). Die potentielle Energie der Konformationen lässt sich durch Separation der Kern- und Elektronenbewegungen mit Hilfe der Born-Oppenheimer Näherung als stetige Funktion der Kernkoordinaten beschreiben. Minima auf der Hyperfläche der Konformationsenergie (Potentialoberfläche des Moleküls) entsprechen stabilen oder Gleichgewichtskonformationen. Den Sattelpunkten können Übergangskonformationen zugeordnet werden. Die Energieunterschiede zwischen den Minima und den Sattelpunkten nennt man Aktivationsenergie. Die Energiehyperfläche des n-Butan hängt nur von einem Torsionswinkel ab (siehe Abb. 4). Die trans-Konformation hat eine Energie, die grössenordnungsmässig ca. 5 kJ / mol niedriger als die der gauche-Rotamere ist und bildet etwa 60 % des gesamten Konformationsensembles.

Das Studium der Potentialoberfläche eines Moleküls mit experimentellen und theoretischen Methoden nennt man Konformationsanalyse. Die Hauptaufgabe der experimentellen Konformationsanalyse besteht in der Messung von Energieunterschieden und Übergangswahrscheinlichkeiten zwischen Konformeren. Dazu eignen sich je nach Objekt verschiedene spektroskopische Methoden wie die Infrarot-Spektroskopie oder die Raman-Spektroskopie, die NMR-Spektroskopie, Ultraschall-Absorptionsmessungen usw.

Die Kenntnis der Potentialoberfläche des Moleküls ist die Grundlage zum Verständnis und zur Vorhersage der physikalischen und chemischen Eigenschaften. Wird die potentielle Energie in eine Taylor-Reihe im Energieminimum K₀ nach den n Freiheitsgraden x_i zerlegt:

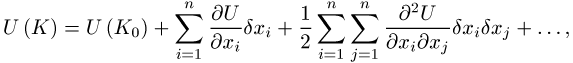
so beschreibt das erste Glied die thermochemischen Eigenschaften, das zweite Glied die Gleichgewichtsgeometrie (die ersten Ableitungen ergeben Null), und das dritte Glied die Frequenzen n_i der Vibrationsspektren in der harmonischen Näherung (die zweite Ableitung ist die Kraftkonstante k_ij). Unter der Annahme kleiner Auslenkungen erhält man die Frequenzen n_i aus der charakteristischen Gleichung

,

wobei (m_ij) die Matrix der Koeffizienten der kinetischen Energie ist, die sich aus den Massen der Atome und den inneren Koordinaten berechnen lässt. Weitere Glieder der Taylor-Zerlegung beschreiben den anharmonischen Charakter der Schwingungen. Makromoleküle haben in Lösungen gewöhnlich eine Vielzahl von Konformationen, während der Konformationsraum im Kristallverband auf eine oder wenige Konformationen beschränkt ist. (statistische Polymerphysik, Konformationsdynamik in Proteinen).

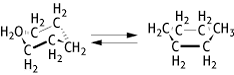
Konformation 1: Konformationen des Zyklohexans: "Sessel" (links) und "Wanne" (rechts).

Konformation 2: Konformationsübergang des Ammoniak.

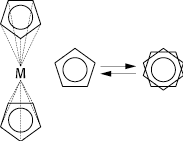
Konformation 3: Rotationsisomerie des Ferrozäns: Übergang von der prismatischen in die antiprismatische Form.

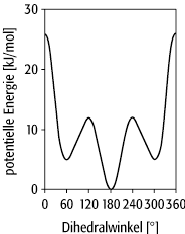
Konformation 4: Änderung der Konformationsenergie des Butans als Funktion des Torsionswinkels.