Parität

Karl-Wilhelm Steinfieber
Teilchenphysik, P, physikalische Grösse, die das Verhalten eines physikalischen Systems gegenüber räumlichen Spiegelungen angibt. Im allgemeinen bezieht sich die Parität auf Spiegelungen an einem Punkt. Man spricht von gerader oder positiver bzw. ungerader oder negativer Parität, wenn das System bei der Spiegelung in sich oder sein Inverses übergeht, und ordnet ihm dann P = +1 bzw. -1 zu. Vektoren bzw. Axialvektoren haben P = -1 bzw. +1; man nennt Axialvektoren daher auch Pseudovektoren. Da die elektrische Feldstärke ein Vektor, die magnetische Feldstärke aber ein Pseudovektor ist, hat ein Plattenkondensator negative, ein Solenoid aber positive Parität.
Die Parität eines zusammengesetzten Systems ist das Produkt
der Einzelparitäten. Die gesamte Parität eines physikalischen Systems bleibt im
allgemeinen erhalten (Paritätserhaltung), lediglich bei schwacher
Wechselwirkung wurde eine Paritätsverletzung gefunden (s. u.). Die Erhaltung
der Parität führt z. B. in der Atomphysik zur Laporteschen Auswahlregel
(Atomspektrum), die besagt, dass sich die Parität bei elektromagnetischer
Dipolstrahlung ändert. Die Parität eines Atoms ist ![]() , wobei
, wobei ![]() , die Quantenzahlen der Bahndrehimpulse der
Elektronen der Atomhülle sind (
, die Quantenzahlen der Bahndrehimpulse der
Elektronen der Atomhülle sind (![]() , Z:
Kernladungszahl).
, Z:
Kernladungszahl).
In den Quantentheorien wird der Paritätsoperation ![]() , die das Vorzeichen aller
Koordinaten in der Wellenfunktion
, die das Vorzeichen aller
Koordinaten in der Wellenfunktion ![]() umkehrt, ein Operator
umkehrt, ein Operator ![]() zugeordnet. Wellenfunktionen
zugeordnet. Wellenfunktionen ![]() mit der Eigenschaft
mit der Eigenschaft ![]() sind Eigenfunktionen der Parität mit
den Eigenwerten
sind Eigenfunktionen der Parität mit
den Eigenwerten ![]() .
Eigenfunktionen des Bahndrehimpulses zum Drehimpulsquadrat
.
Eigenfunktionen des Bahndrehimpulses zum Drehimpulsquadrat ![]() haben die Parität
haben die Parität ![]() .
.
In der Quantenfeldtheorie bezieht man die Parität auf den
Vakuumzustand ![]() , der als
invariant gegenüber
, der als
invariant gegenüber ![]() vorausgesetzt
wird:
vorausgesetzt
wird: ![]() . Dann gilt für
einen Einteilchenzustand
. Dann gilt für
einen Einteilchenzustand ![]() mit
der Energie E und dem Impuls
mit
der Energie E und dem Impuls ![]() :
: ![]() wobei
wobei ![]() ein Phasenfaktor ist. Bei Teilchen mit
ganzzahligem Spin (
ein Phasenfaktor ist. Bei Teilchen mit
ganzzahligem Spin (![]() ),
die durch die eindeutigen Darstellungen - die Tensordarstellungen - der
dreidimensionalen räumlichen Drehgruppe beschrieben werden, entspricht die
zweimalige Anwendung von
),
die durch die eindeutigen Darstellungen - die Tensordarstellungen - der
dreidimensionalen räumlichen Drehgruppe beschrieben werden, entspricht die
zweimalige Anwendung von ![]() der
Identität:
der
Identität: ![]() , und es gilt
, und es gilt
![]() ; bei Teilchen mit
halbzahligem Spin (s = n + 1/2), die durch die zweideutigen
Darstellungen - die Spinordarstellungen - der dreidimensionalen räumlichen
Drehgruppe beschrieben werden, gilt bei zweimaliger Anwendung von
; bei Teilchen mit
halbzahligem Spin (s = n + 1/2), die durch die zweideutigen
Darstellungen - die Spinordarstellungen - der dreidimensionalen räumlichen
Drehgruppe beschrieben werden, gilt bei zweimaliger Anwendung von ![]() entweder
entweder ![]() oder
oder ![]() , und es gilt
, und es gilt ![]() . Daher haben Teilchen mit ganzzahligem Spin
(Bosonen) die innere Parität oder Eigenparität
. Daher haben Teilchen mit ganzzahligem Spin
(Bosonen) die innere Parität oder Eigenparität ![]() , Teilchen mit halbzahligem Spin (Fermionen)
, Teilchen mit halbzahligem Spin (Fermionen) ![]() relativ zum Vakuum.
Spinlose Teilchen mit
relativ zum Vakuum.
Spinlose Teilchen mit ![]() bzw.
-1 nennt man skalare bzw. pseudoskalare
Teilchen, Teilchen mit Spin s = 1 und
bzw.
-1 nennt man skalare bzw. pseudoskalare
Teilchen, Teilchen mit Spin s = 1 und ![]() bzw. +1 Vektor- bzw. Pseudovektorteilchen. Da
die innere Parität nur als relative Parität definiert und die Parität des
Vakuums nicht beobachtbar ist, können die verschiedenen relativen Paritäten der
Elementarteilchen nur über ihre gegenseitigen Wechselwirkungen bestimmt werden.
Die Superauswahlregeln schränken diese Vergleichbarkeit ein, so dass man für
Bosonen und Fermionen je eine willkürliche Wahl treffen muss: Man legt die Parität
des
bzw. +1 Vektor- bzw. Pseudovektorteilchen. Da
die innere Parität nur als relative Parität definiert und die Parität des
Vakuums nicht beobachtbar ist, können die verschiedenen relativen Paritäten der
Elementarteilchen nur über ihre gegenseitigen Wechselwirkungen bestimmt werden.
Die Superauswahlregeln schränken diese Vergleichbarkeit ein, so dass man für
Bosonen und Fermionen je eine willkürliche Wahl treffen muss: Man legt die Parität
des ![]() -Mesons mit P = -1, die des
Protons mit P = +1 fest (Elementarteilchen, Tab.
1-3); die relative Parität von Teilchen desselben Ladungsmultipletts kann man
willkürlich zu +1 festlegen.
-Mesons mit P = -1, die des
Protons mit P = +1 fest (Elementarteilchen, Tab.
1-3); die relative Parität von Teilchen desselben Ladungsmultipletts kann man
willkürlich zu +1 festlegen.
Bis 1956 war man von der Erhaltung der Parität in der Natur
überzeugt und betrachtete daher nur spiegelungsinvariante Ansätze für die
Wechselwirkungen. Im Zusammenhang mit der Klärung des ![]() -
-![]() -Rätsels im System der neutralen K-Mesonen
wiesen Lee und Yang darauf hin, dass keine experimentelle Begründung für diese
Annahme vorliegt und daher bestimmte physikalische Vorgänge, z.B. Umwandlungen,
Zerfälle und Erzeugungen, und deren spiegelbildliche Ausführung nicht notwendig
gleich wahrscheinlich sein müssen (Kaon). Tatsächlich wurde von Frau Wu und
ihren Mitarbeitern 1957 am
-Rätsels im System der neutralen K-Mesonen
wiesen Lee und Yang darauf hin, dass keine experimentelle Begründung für diese
Annahme vorliegt und daher bestimmte physikalische Vorgänge, z.B. Umwandlungen,
Zerfälle und Erzeugungen, und deren spiegelbildliche Ausführung nicht notwendig
gleich wahrscheinlich sein müssen (Kaon). Tatsächlich wurde von Frau Wu und
ihren Mitarbeitern 1957 am ![]() -Zerfall des 60Co eine Verletzung der Parität nachgewiesen
(Wu-Experiment), die auch anderweitig mehrfach bestätigt wurde: 60Co zerfällt in 60Ni unter Emission eines
Elektrons
-Zerfall des 60Co eine Verletzung der Parität nachgewiesen
(Wu-Experiment), die auch anderweitig mehrfach bestätigt wurde: 60Co zerfällt in 60Ni unter Emission eines
Elektrons ![]() und eines
Antineutrinos
und eines
Antineutrinos ![]() gemäss
gemäss ![]() . Bei diesem
. Bei diesem ![]() -Übergang ändert sich der Kernspin um
den Betrag
-Übergang ändert sich der Kernspin um
den Betrag ![]() , wobei
sowohl das Elektron als auch das Antineutrino einen Spin vom Betrag
, wobei
sowohl das Elektron als auch das Antineutrino einen Spin vom Betrag ![]() mit sich führen. Da der Spin
ein Axialvektor ist, wird er hier zweckmässig als Drehsinn charakterisiert, der
sich bei Spiegelung offensichtlich nicht ändert. Vernachlässigt man die Masse
des Elektrons, dann weist sein Spin entweder in Richtung (Rechtsschraube) oder
entgegen der Richtung (Linksschraube) seines Impulses; der Spin des
(masselosen) Antineutrinos weist dagegen stets in Richtung seines Impulses
(Rechtsschraube): Es sind daher beide Zerfallsschemata der Abb. denkbar. Das
Wu-Experiment, bei dem die mit dem Kernspin verkoppelten magnetischen Momente
des 60Co in
einem schwachen äusseren Magnetfeld bei sehr tiefen Temperaturen ausgerichtet
wurden, zeigte, dass etwa 30 % mehr Elektronen entgegen (siehe Abb. 1a) als in
Richtung (siehe Abb. 1b) des Kernspins emittiert wurden; die Antineutrinos
wurden nicht registriert. Da bei Spiegelungen eine Rechts- in eine
Linksschraube übergeht und umgekehrt, bedeutet dies eine Verletzung der Parität.
Die gemessene Richtungsverteilung der Elektronen stimmt mit der theoretisch
unter Berücksichtigung dieser Paritätsverletzung und der von Null verschiedenen
Elektronenmasse zu erwartenden Verteilung genau überein.
mit sich führen. Da der Spin
ein Axialvektor ist, wird er hier zweckmässig als Drehsinn charakterisiert, der
sich bei Spiegelung offensichtlich nicht ändert. Vernachlässigt man die Masse
des Elektrons, dann weist sein Spin entweder in Richtung (Rechtsschraube) oder
entgegen der Richtung (Linksschraube) seines Impulses; der Spin des
(masselosen) Antineutrinos weist dagegen stets in Richtung seines Impulses
(Rechtsschraube): Es sind daher beide Zerfallsschemata der Abb. denkbar. Das
Wu-Experiment, bei dem die mit dem Kernspin verkoppelten magnetischen Momente
des 60Co in
einem schwachen äusseren Magnetfeld bei sehr tiefen Temperaturen ausgerichtet
wurden, zeigte, dass etwa 30 % mehr Elektronen entgegen (siehe Abb. 1a) als in
Richtung (siehe Abb. 1b) des Kernspins emittiert wurden; die Antineutrinos
wurden nicht registriert. Da bei Spiegelungen eine Rechts- in eine
Linksschraube übergeht und umgekehrt, bedeutet dies eine Verletzung der Parität.
Die gemessene Richtungsverteilung der Elektronen stimmt mit der theoretisch
unter Berücksichtigung dieser Paritätsverletzung und der von Null verschiedenen
Elektronenmasse zu erwartenden Verteilung genau überein.
Das Standardmodell der Elementarteilchenphysik beschreibt die
Kopplung von Fermionen an die schwachen Vektorbosonen durch Terme, die die
Parität maximal verletzen. Beispielsweise lautet der Anteil der
Lagrange-Dichte, welcher die Wechselwirkung von Elektron, seinem Antineutrino
und dem W-Boson beschreibt: ![]()
Der Operator ![]() verhält sich unter Lorentz-Transformationen wie
ein Vektor-Axialvektor (»V-A«) und verletzt dabei die Parität maximal.
verhält sich unter Lorentz-Transformationen wie
ein Vektor-Axialvektor (»V-A«) und verletzt dabei die Parität maximal.
Die Paritätsverletzung in der schwachen Wechselwirkung hat zur
Folge, dass masselose Fermionen - in der Praxis trifft dies auf die Neutrinos
zu, selbst wenn sie eine kleine, nichtverschwindende Ruhemasse haben sollten -
stets eine definierte Helizität haben: es gibt nur rechtshändige Antineutrinos
und linkshändige Neutrinos, aber ein rechtshändiges Neutrino existiert in der
Natur nicht. Somit besteht in der Natur ein fundamentaler Unterschied zwischen
links und rechts. Der Übergang rechtshändiges Antineutrino ![]() linkshändiges Neutrino ist jedoch
invariant unter der kombinierten Symmetrietransformation
linkshändiges Neutrino ist jedoch
invariant unter der kombinierten Symmetrietransformation ![]() , also der nacheinander ausgeführten
Transformation von Ladungskonjugation
, also der nacheinander ausgeführten
Transformation von Ladungskonjugation ![]() und Spiegelung
und Spiegelung ![]() . In der schwachen Wechselwirkung wird also auch
die Symmetrie unter der Ladungskonjugation
. In der schwachen Wechselwirkung wird also auch
die Symmetrie unter der Ladungskonjugation ![]() , der
, der ![]() -Parität, verletzt. Die CP-Symmetrie ist
hingegen eine fast immer erhaltene Symmetrie; CP-Verletzung wird bisher nur im
System der neutralen K-Mesonen beobachtet.
-Parität, verletzt. Die CP-Symmetrie ist
hingegen eine fast immer erhaltene Symmetrie; CP-Verletzung wird bisher nur im
System der neutralen K-Mesonen beobachtet.
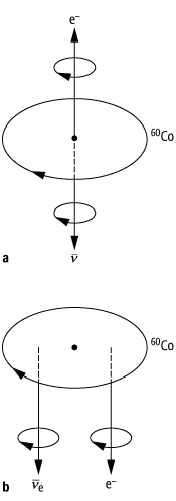
Parität: Das Wu-Experiment.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.