Techniklexikon

Bändermodell

Energiebändermodell. Darstellung der erlaub ten und verbotenen Energiebereiche für die Elektronen, wobei deren Energie entlang einer senkrechten Achse aufgetragen wird. In der Halbleiterphysik kommt dem B. der Kristallelektronen eine zentrale Bedeutung zu. Es erklärt, wie sich die Elektronen in einem » Festkörper bez. ihrer Energie anordnen und unter dem Einfluß äußerer Einwirkungen (z. B. Temperatur, elektrische Felder) verhalten. Die Entstehung von Energiebändern läßt sich vereinfacht folgendermaßen verstehen: Nach der Quantentheorie kann ein angeregtes Elektron (Anregung) in einem einzelnen Atom nicht jeden beliebigen Energiewert annehmen, sondern nur diskrete Energieniveaus besetzen, die einen relativ großen Abstand haben. Nähern sich zwei Atome einander so weit, daß sie sich gegenseitig „spüren", d.h. elektrisch miteinander wechselwirken (Molekülbildung), verdoppelt sich die Anzahl dieser erlaubten Energieniveaus durch Aufspaltung, wobei sich ihr Abstand zueinander verringert. Im Festkörper befindet sich nun aufgrund der Kristallstruktur eine sehr große Anzahl von Atomen (etwa 1022 je cm3) so dicht beieinander, daß eine intensive Wechselwirkung stattfinden kann, wodurch jedes Energieniveau in 1022 Unterniveaus aufspaltet. Diese „Verschmierung" führt zu breiten, quasikontinuierlichen Energiebereichen, den Energiebändern. Zwischen den einzelnen Bändern liegen Bandlücken, d. h. energetisch verbotene Bereiche, in denen sich keine Energieniveaus befinden (Energielücken). Die Breite der erlaubten Energiebänder und die Bandabstände zwischen ihnen sind bei jedem Festkörper verschieden und für ihn charakteristisch. In einem idealen Kristallgitter sind alle Elektronen an der Valenzbindung beteiligt, d. h. gebunden. Das oberste Energieband, das beim absoluten Temperaturnullpunkt (7= OK) noch von den bindenden Elektronen (Valenzelektronen) besetzt wird, heißt Valenzband. Seine Oberkante wird mit E^ bezeichnet. Das nächsthöhere erlaubte Energieband wird Leitungsband (mit der Leitungsbandunterkante EL) genannt, da es die durch Generation erzeugten freien Elektronen aufnimmt (Leitungselektronen). Zwischen ihnen liegt ein verbotener Energiebereich (Zone, verbotene), dessen Breite als Bandabstand £g = £L - Ey bezeichnet wird. In einem idealen Kristall wird die verbotene Zone durch das Fermi-Niveau in zwei gleich große Abschnitte geteilt. Bei der bildlichen Darstellung des B. in horizontalen Energiebandanordnungen hat die Abszisse (waagerechte Achse) keine Bedeutung, da die Elektronen in einem ungestörten Halbleiter prinzipiell örtlich nicht lokalisiert sind, sich also mit gleicher Wahrscheinlichkeit an jeder Stelle des Kristalls befinden können. Dagegen sind Elektronen in den örtlich festsitzen den Störstellen ebenfalls an den Ort der Störstelle gebunden. Ähnliches trifft bei Grenzflächen, Oberflächen usw. zu. In diesen Fällen ist es oft üblich, das B. zum Energiebandschema zu erweitern und die Abszisse mit einer Ortskoordinate zu versehen. Grundsätzlich sind alle Elektronen bestrebt, den für sie energetisch günstigsten Zustand einzunehmen, also Niveaus mit niedrigen Energiewerten zu besetzen. Deshalb stellt sich ohne äußere Einflüsse stets ein Gleichgewichtszustand ein, d. h., die energetisch tiefer liegenden Niveaus sind immer voll aufgefüllt und somit stärker besetzt als die höher liegenden. Durch energetische Anregung (Temperatur, Strahlung, elektrische Felder) kann diese Normalbesetzung bis zur Inversion verändert werden. Auf derartigen Vorgängen beruht die gesamte Halbleiterelektronik. Modell zur Beschreibung des elektronischen Spektrums im Festkörper mittels Energiebändern. Das Energiespektrum eines Elektrons im idealen Kristall wird durch die Bandstruktur gekennzeichnet. Für Nichtmetalle erfolgt die Beschreibung der Energiezustände durch Leitungs- und Valenzbänder, in denen sich Elektronen befinden können, und die durch eine Energielücke (Bandlücke) voneinander getrennt sind, die für die Elektronen eine verbotene Zone darstellt.

Die Bänder werden von unten mit Elektronen gefüllt, wobei das Pauli-Prinzip beachtet werden muss; das heisst, in vollbesetzten Band ist zu jedem Impuls auch der entgegengesetzte Impuls vorhanden. Deshalb ist in einem vollbesetzten Band keine Bewegung des Ladungsschwerpunkts und damit auch kein Stromfluss möglich. Ist bei der Energie, bis zu der Elektronen in die Bänder gefüllt werden, dem Fermi-Niveau, ein Band nicht abgeschlossen, oder besteht ein Überlapp zwischen den Bändern, dann kann auch bei 0K bei Anlegen einer elektrischen Spannung Strom fliessen, indem Elektronen in die nächst höheren Energiezustände im Band angeregt werden, wozu keine Aktivierungsenergie nötig ist. Im Gegensatz dazu muss bei abgeschlossenen Bändern eine Aktivierungsenergie aufgewendet werden, damit Strom fliessen kann; das Material leitet also bei 0K nicht.

Bei Nichtmetallen liegt die Fermi-Energie innerhalb der Energielücke, also zwischen Valenz- und Leitungsband. Ebenfalls innerhalb der Bandlücke können bei dotierten Halbleitern Energiezustände liegen, die von den Störstellen herrühren (Akzeptor, Donator). Das absolute energetische Maximum der Valenzbänder heisst Valenzbandkante, das absolute Minimum der Leitungsbänder Leitungsbandkante. Die energetische Differenz beider Bandkanten ist die Breite der verbotenen Zone.

Der Unterschied zwischen Isolatoren und Halbleitern ist der, dass beim Halbleiter bei Raumtemperatur die thermische Energie ausreicht, um Eigenleitung (intrinsischer Halbleiter) zu erzeugen, das heisst, Elektronen aus dem Valenzband in das nächst höhere Leitungsband zu aktivieren, während bei Isolatoren die Energielücke zu gross ist.

Bei endlichen Temperaturen sind in n-Halbleitern einzelne Elektronen in das Leitungsband angeregt, die sich vorwiegend an der Bandkante befinden. Sie verhalten sich wie nahezu freie Elektronen, nehmen am Stromtransport teil und tragen so zur Leitfähigkeit bei. Bei Silicium und Germanium beispielsweise liegt die Leitungsbandkante nicht beim Wellenvektor k = 0, so dass die Elektronen sich an unterschiedlichen Stellen ("Tälern") in der Brillouin-Zone befinden (Abb. 1). Man hat es mit einem Mehrtalhalbleiter zu tun. Die Flächen konstanter Energie sind langgezogene Rotationsellipsoide (Fermi-Fläche). In p-Halbleitern sind bei endlichen Temperaturen einzelne Elektronen angeregt und hinterlassen Löcher, die sich vorwiegend an der Bandkante befinden. Die Löcher verhalten sich wie nahezu freie positive Ladungsträger, nehmen am Stromtransport teil und tragen so zur Leitfähigkeit bei.

Die Valenzbandkante vieler Halbleiter befindet sich bei k = 0 und ist meist mehrfach entartet. Für Germanium und Silicium ist die Kante des Valenzbandes zweifach entartet. Die Flächen für E = const. sind daher selbst für kleine k nicht Kugeln, sondern ähneln Würfeln im oberen Band bzw. Oktaedern im unteren Band (Abb. 2, Fermi-Fläche).

Im oberen Band haben die Löcher eine grössere effektive Masse als im unteren. Man unterscheidet schwere und leichte Löcher. Das dritte Band liegt infolge von Spin-Bahn-Kopplung tiefer.

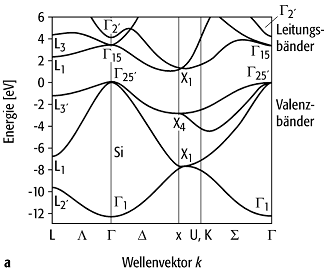
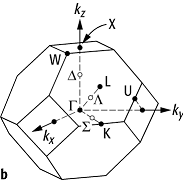
Bändermodell 1: a) Darstellung der Energiebänder für Silicium als Funktion des Wellenzahlvektors k für ausgewählte Kristallrichtungen in der Brillouin-Zone, die in b) dargestellt sind.

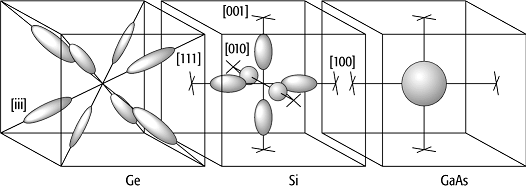
Bändermodell 2: Flächen konstanter Energie für die Halbleiter Ge, Si und GaAs. Die Symmetrie der Energieflächen der indirekten Halbleiter Si und Ge ist sehr viel komplizierter als für den direkten Halbleiter GaAs.