Techniklexikon

Dirac-Gleichung

QuantenmechanikTeilchenphysik, relativistische Wellengleichung für Teilchen mit der Masse m und dem Spin s = 1/2. In kovarianter Schreibweise hat sie die Form

                 (1)

mit dem Lorentz-Index m = 0, 1, 2, 3, ,  und den Diracschen g-Matrizen g^m , die sich durch 4 ´ 4-Matrizen darstellen lassen, die auf die vierkomponentige Wellenfunktion des Dirac-Feldes y(x) wirken (Dirac-Matrizen):

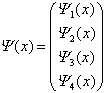
mit x = (ct, r). Dementsprechend handelt es sich bei der Dirac-Gleichung um ein System von vier Gleichungen, dessen (freie) Lösungen die beiden Spineinstellungen  von Teilchen (Lösung positiver Energie) und Antiteilchen (Lösung negativer Energie) beschreiben.

Die Dirac-Gleichung ist die fundamentale Gleichung zur Beschreibung aller fermionischen Elementarteilchen, damit also, gemäss dem Standardmodell der Elementarteilchen, aller Materie; sie ist die grundlegende Bewegungsgleichung nicht nur der relativistischen Einteilchen-Quantenmechanik, sondern auch der Quantenfeldtheorien der Fermionfelder (Quantenelektrodynamik, Glashow-Weinberg-Salam-Modell der elektroschwachen Wechselwirkung und Quantenchromodynamik).

Die Dirac-Gleichung hat axiomatischen Charakter, sie kann also, gleich der nichtrelativistischen Schrödinger-Gleichung, nicht streng bewiesen werden, lässt sich jedoch mit Hilfe der relativistischen Beziehung zwischen Energie E = cp₀ und Impuls p des Teilchens motivieren, wenn man letztere gemäss

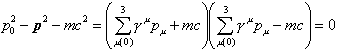
in das Produkt zweier Ausdrücke zerlegt, die linear in E und p sind; dadurch wird die Analogie zur Schrödinger-Gleichung hergestellt, die die Energie ebenfalls nur linear enthält. Die Diracschen g-Matrizen g^m müssen dabei den Relationen

,               (2)

mit dem pseudoeuklidischen metrischen Tensor g^mn genügen (g⁰⁰ =  - g¹¹ =  - g²² - g³³ = 1, g^mn = 0 für m ¹ n). Ersetzt man nun p_m durch , so folgt direkt die Dirac-Gleichung (1).

Schreibweisen der Dirac-Gleichung:

1) In Komponentenschreibweise lautet die Dirac-Gleichung

mit a,b = 1, 2, 3, 4, wobei über doppelt auftretende Indizes jeweils summiert wird.

2) Dirac-Slash-Schreibweise: insbesondere in der Elementarteilchenphysik gebräuchlich ist die Form der Dirac-Gleichung in natürlichen Einheiten  = c = 1 und der Konvention  für einen beliebigen Vierervektor a_m. Mit  und dem Ansatz für ein freies Teilchen  ergibt sich

,

wobei der Viererspinor u unabhängig von x ist.

3) Bei der Suche nach Energieeigenzuständen ist es bequem, die Form

mit dem Hamilton-Operator H und b = g⁰, a_k = bg^k zu verwenden.

Verhalten unter Lorentz-Transformationen:

Bei Lorentz-Transformationen  muss die Dirac-Gleichung forminvariant (relativistisch kovariant) sein. Daher transformieren sich y(x) und g^m gemäss . Die Grössen S(L) bilden eine Spinordarstellung der Lorentz-Gruppe; sie sind 4 ´ 4-Matrizen, die der Relation  genügen müssen.

Andererseits ist die Gleichung (2) bei beliebigen nichtsingulären Transformationen  invariant. Die konkrete Darstellung der Dirac-Matrizen ist daher nur bis auf derartige Transformationen festgelegt.

Die Grösse  genügt der Kontinuitätsgleichung , wobei

positiv definit und  mit

ist; r kann daher als Wahrscheinlichkeitsdichte und j als Wahrscheinlichkeitsstrom im Sinne der Schrödingerschen Wellenmechanik interpretiert werden.

Die kräftefreie Dirac-Gleichung ist invariant unter räumlichen Spiegelungen  (Paritätstransformation). Verzichtet man auf diese Invarianz, so genügen bei verschwindender Ruhemasse bereits zweikomponentige Spinoren zur Beschreibung dieser Teilchen (z.B. Neutrinos). (Weyl-Gleichung, Chiralität)

Lösungen der freien Dirac-Gleichung:

Die Dirac-Gleichung hat ebene Wellen der

Gestalt  mit  zur Lösung, wobei u(p) ein Viererspinor ist, der der Dirac-Gleichung im Impulsraum  genügt.

Da  sowohl positiv als

auch negativ sein kann, erhält man vier linear unabhängige Lösungen für u(p) und damit vier linear unabhängige Lösungen der Dirac-Gleichung; führt man  ein, so lauten diese

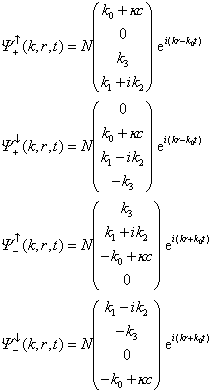
mit dem Normierungsfaktor .

Die ersten beiden Lösungen gehören zu positiver Energie und Spin + 1/2 bzw.  - 1/2, wie sich aus ihrem Verhalten unter Rotationen ergibt; die letzten beiden Lösungen gehören dementsprechend zu negativer Energie und Spin + 1/2 bzw. - 1/2. Die Lösungen zu negativer Energie erfordern eine sorgfältige Interpretation. Eine konsistente Beschreibung ist möglich im Rahmen relativistischer Quantenfeldtheorien mit Erzeugungs- und Vernichtungsoperatoren für Teilchen- und Antiteilchenzustände (zweite Quantisierung). Eine frühe Interpretation der Antiteilchen-Zustände geht auf Dirac zurück und führte zur theoretischen Vorhersage des Positrons (Dirac-See) (Diracsche Theorie des Elektrons). [BK1]