Techniklexikon

Kristallstrukturanalyse

Biophysik, Röntgenstrukturanalyse, Feinstrukturanalyse, Verfahren zur Bestimmung der Atomanordnung im Kristallgitter durch Röntgen-, Elektronen- oder Neutronenstrahlen (ionisierende Strahlung). Die Wellenlängen dieser Strahlen liegen etwa im Bereich der Atomabstände im Kristallgitter (0,1 nm), welches deshalb als räumliches Beugungsgitter wirkt und Interferenzen erzeugt. Aus der Lage und Stärke der Interferenzmaxima (»Reflexe«) wird die über den Untersuchungszeitraum gemittelte Struktur des beugenden Kristalls bestimmt. Eine vollständige Kristallstrukturanalyse liefert die Koordinaten der Atome aller im Kristall enthaltenen Moleküle relativ zu den Basisvektoren der (sich periodisch wiederholenden) Elementarzelle und Parameter der i.a. anisotropen Wärmeschwingungen der Atome. Aus den Atomkoordinaten ergibt sich die Atomanordnung im Kristall, man erhält sowohl Aussagen über die gegenseitige Anordnung von Molekülen (z.B. Koordinationszahlen von Ionen, Atomabstände) als auch über die innere Struktur jedes Moleküls (Bindungslängen, Valenzwinkel, Konformation). Letztere Information ist die Voraussetzung für quantenchemische Berechnungen an komplizierten Molekülen. Aus Atomabständen und den Schwingungsparametern lassen sich auch Schlüsse auf die Kräfte zwischen Molekülen ziehen.

Lange Zeit war die Kristallstrukturanalyse, insbesondere die Röntgenstrukturanalyse, die einzige Methode zur Strukturaufklärung mit atomarer Auflösung. Damit wurde sie zur Grundlage der Stereochemie ganzer Substanzklassen in der organischen Chemie und ein wichtiges Hilfsmittel in der Materialforschung (z.B. Untersuchung von Legierungen). Eine herausragende Bedeutung hat die Kristallstrukturanalyse bei der Strukturaufklärung von Biomakromolekülen, besonders von Proteinen. Erst in den 80er und 90er Jahren erreichte die NMR-Spektroskopie eine solche Entwicklung, dass sie auf atomarem Niveau als alternative Methode zur Strukturaufklärung von grossen Molekülen in (konzentrierter) Lösung anwendbar wurde. Die hochauflösende NMR-Spektroskopie ist besonders in solchen Fällen ein Ausweg, wo kein Kristall des zu untersuchenden Stoffes erzeugt werden kann (das Hauptproblem bei der Anwendung der Kristallstrukturanalyse) oder wo Unterschiede zwischen den Molkülkonformationen im Kristall und in Lösung vorliegen. Methodik-Aufnahmemethoden: Man unterscheidet Einkristall-, Faser- und Pulvermethoden, je nachdem ob ein Einkristall, ein polykristallines Material (Pulver) oder eine Faser (Ausrichtung linearer Moleküle entlang einer Achse) untersucht wird. Die ältesten Aufnahmen wurden 1912 durch M. v. Laue, W. Friedrich und P. Knipping an anorganischen Einkristallen mit weissem (polychromatischem) Röntgenlicht gemacht (Laue-Methode). Beim Bragg- oder Drehkristallverfahren (W.H. Bragg, 1913) wird ein Einkristall mit monochromatischen Röntgenstrahlen einer Kathodenstrahlröhre bestrahlt, während es um eine Achse dauernd gedreht wird. Diese Achse liegt in der zu untersuchenden Fläche und senkrecht zum Primärstrahl. Nach der Art der Registrierung der Streuungsintensitäten unterscheidet man Film-, Zählrohr- oder Diffraktometermethoden. Bei den sogenannten Goniometerverfahren wird die Bewegung des Untersuchungsobjektes mit einer Bewegung des Aufzeichnungsmediums kombiniert (»Bewegt-Film-Methoden«). Meist werden zur Kristallstrukturanalyse einer Substanz mehrere Aufnahmetechniken benutzt. Wird als Quelle der Röntgenstrahlen ein Synchrotron genutzt, kann die Untersuchungszeit wegen der hohen Intensität des Röntgenstrahls bis in den Sekundenbereich reduziert werden (Synchrotron-Röntgenstrukturanalyse). Methodik-Auswertung des Steuungsbildes (Diffraktogramms): Der Weg vom Streuungsbild bis zur aufgelösten Struktur lässt sich gedanklich in 4 Etappen untergliedern.

1. Bestimmung der Basisvektoren und der Raumgruppe des Kristalls. Hierbei stützt man sich auf die Lage der Reflexe im Diffraktogramm, systematische Auslöschungen und die Symmetrie der Verteilung der Streuungsintensitäten. Die Reflexe werden indiziert, d.h. mit Indizes  und  versehen. Der Streuungsvektor  ist definiert als Differenz der Einheitsvektoren des gestreuten und des einfallenden Strahles in Einheiten der reziproken Wellenlänge l. Streuungsmaxima entstehen nur bei ganzzahligen Indizes.

2. Ein Elektron am Koordinatenursprung wird eine Streuungswelle E(S) erzeugen, ein Elektron am Ort r die Welle . Die Amplitude der Streuungswelle des realen Kristalls relativ zur Welle eines Elektrons am Koordinatenursprung wird Strukturfaktor

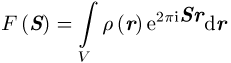
genannt. Hierbei sind r(r) die Elektronendichteverteilung und V das Volumen der Elementarzelle. Aus den experimentellen integralen Streuungsintensitäten  der Reflexe hkl werden werden die Betragsquadrate der im allgmeinen komplexen Strukturfaktoren  über eine Proportionalitätsbeziehung berechnet, wobei sich der Faktor aus Gittereigenschaften und der experimentellen Anordnung ergibt. 3. Die Berechnung der Elektronendichteverteilung

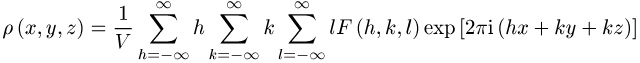
ist durch Fouriertransformation aus den Strukturfaktoren  möglich. Die Lagen der Atome entsprechen dann den Maxima der Elektronendichte. Dabei treten aber folgende Probleme auf: Erstens sind aus den Streuungsdaten nur die Beträge |F| direkt bekannt, die Phasen a müssen aus alternativen Betrachtungen gefunden werden. Zweitens kann die Summation nicht über alle Reflexe, sondern nur über den experimentell zugänglich Teil der Indextripel durchgeführt werden. Praktisch wird die Dichteverteilung mit sukzessiven Näherungen bestimmt, bei denen eine zunehmende Zahl von Reflexen und Phasen berücksichtigt wird. Der Ausgangspunkt sind besonders starke Reflexe, die besonders stark streuenden Atomen entsprechen.

4. Für die Modellstruktur einer bestimmten Iterationsstufe werden die zu erwartenden theoretischen Strukturfaktoren

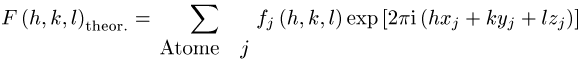
berechnet. Hierbei ist  eine tabellierte Funktion von Atomformfaktoren, welche die Streufähigkeit der Atomtypen beschreibt. Eine Möglichkeit zur Bestimmung der Anfangsphasen besteht in der Substitution von Atomen durch chemisch gleichwertige, aber wesentlich stärker streuende Atome (Methode der multiplen isomorphen Substitution). Eine andere Variante ist die Verwendung zweier unterschiedlicher Wellenlängen des Primärstrahls, bei dem sich der Atomformfaktor einer Sorte Atome stark ändert (Methode der anomalen Streuung).Besonderheit bei grossen Molekülen: Eine vollständige Kristallstrukturanalyse gelingt nur, wenn die Anzahl der gemessenen Intensitäten mindestens 5mal so gross wie die Anzahl der bestimmenden Atomkoordinaten ist. Bei sehr grossen Molekülen reicht die Information des Diffraktogramms oft nicht aus, um unabhängig die Lage aller Atome zu bestimmen. Hier behilft man sich beim Modellbau mit zusätzlichen Daten wie der Atomgeometrie in kleineren Modellverbindungen, stereochemischen Gesetzmässigkeiten oder sogar der unabhängigen Bestimmung ganzer Substrukturen in Teilen der grossen Moleküle. Auch durch die Annahme isotroper Temperaturfaktoren wird die Zahl der Freiheitsgrade des Modells reduziert.

Für viele langgestreckte Biomakromoleküle (DNS oder Faserproteine) gelingt es nur, Kristalle mit Ordnung entlang einer Achse zu erzeugen. Die Diffraktogramme werden dann Faserdiagramme genannt, welche bei der Auswahl unter verschiedenen helikalen Modellen der Fasermoleküle eine Entscheidungshilfe bieten. Besonderheiten bei verschiedenen Strahlenarten: Röntgenstrahlen werden durch die Elektronenschalen, Elektronenstrahlen durch das elektrostatische Feld und Neutronenstrahlen durch die Atomkerne und die magnetischen Momente der Elektronenhülle gebeugt. Deshalb sind die Formfaktoren bei verschiedenen Strahlenarten unterschiedlich. So lassen sich Atome niedriger Ordnungszahl (besonders Wasserstoff) bei der Röntgenkristallstrukturanalyse fast nicht, mit der Elektronen- oder Neutronenbeugung aber gut lokalisieren. Dafür stellen letztere Methoden besondere Anforderungen an die Einkristalle. Für die Elektronenbeugung benötigt man im Vakuum beständige, genügend grosse, aber flache (< 10 mm) Kristalle. Das Kristallvolumen bei der Neutronenbeugung sollte 1 mm³ nicht unterschreiten. Oft gelingt es durch die komplementäre Information verschiedener Methoden, zu einem vollständigeren Strukturmodell zu gelangen.