Schwarze Löcher

Irene Kramer-Schwenk
Relativitätstheorie
und GravitationAstronomie und Astrophysik, Objekte, die so kompakt sind, dass
nicht einmal Licht ihrem Gravitationsfeld entweichen kann. Ihre Existenz ist
eine Vorhersage der Allgemeinen Relativitätstheorie. Allgemein werden Schwarze
Löcher durch Gebiete der Raumzeit charakterisiert, die nie in die Vergangenheit
äusserer Beobachter gelangen und durch einen Ereignishorizont von diesen
abgeschirmt sind. Aus dem Bereich innerhalb des Ereignishorizontes können keine
Signale nach aussen dringen. Gemäss der Allgemeinen Relativitätstheorie sollte
sich im Innern eines Schwarzen Loches eine Singularität befinden. Es wird
vermutet, dass solche Singularitäten nie ohne Ereignishorizont existieren.
Allerdings wurde dieses Prinzip der kosmischen Zensur (keine »nackten
Singularitäten«) bisher nicht mathematisch streng bewiesen. Mathematische
Theoreme zeigen, dass stationäre Schwarze Löcher durch drei Parameter
vollständig charakterisiert sind: Masse ![]() , Drehimpuls
, Drehimpuls ![]() und elektrische Ladung
und elektrische Ladung ![]() (»Schwarze Löcher haben keine Haare«).
(»Schwarze Löcher haben keine Haare«).
Im einfachsten Fall sphärischer Symmetrie werden Schwarze
Löcher durch die Schwarzschild-Metrik beschrieben, eine Lösung der Einstein-Gleichungen
im Vakuum (![]() ):
):
![]()
wobei ![]() das Linienelement auf der zweidimensionalen
Kugel ist. Die Singularität bei
das Linienelement auf der zweidimensionalen
Kugel ist. Die Singularität bei ![]() ist eine physikalische Singularität, während
die Singularität beim Schwarzschild-Radius
ist eine physikalische Singularität, während
die Singularität beim Schwarzschild-Radius ![]() eine Koordinatensingularität ist;
eine Koordinatensingularität ist; ![]() gibt die Lage des Ereignishorizontes an. Ein
Beobachter, der durch diesen Horizont fällt, trifft in endlicher Eigenzeit auf
die Singularität (die Eigenzeit vom Horizont bis zur Singularität beträgt für
freien Fall
gibt die Lage des Ereignishorizontes an. Ein
Beobachter, der durch diesen Horizont fällt, trifft in endlicher Eigenzeit auf
die Singularität (die Eigenzeit vom Horizont bis zur Singularität beträgt für
freien Fall ![]() ). Wenn man den
räumlichen Teil der Schwarzschild-Metrik (um eine Dimension verringert) in
einen dreidimensionalen Anschauungsraum einbettet, erhält man die
Einstein-Rosen-Brücke (siehe Abb. bei Wurmlöcher). Sie enthält zwei
asymptotisch-flache Räume, die durch einen Schlund (»Wurmloch«) miteinander
verbunden sind. Ein reales Schwarzes Loch entsteht durch Kollaps eines Objektes
(z.B. eines massiven Sterns) auf eine Singularität (siehe Abb. 1, wo durch die
Lage der Lichtkegel zum Ausdruck gebracht wird, dass Signale, die innerhalb des
Ereignishorizontes ausgesandt werden, nie in den Aussenraum gelangen können).
Das von der Oberfläche des kollabierenden Sterns abgestrahlte Licht kommt bei
dem entfernten Beobachter rotverschoben an, wobei die Rotverschiebung durch
). Wenn man den
räumlichen Teil der Schwarzschild-Metrik (um eine Dimension verringert) in
einen dreidimensionalen Anschauungsraum einbettet, erhält man die
Einstein-Rosen-Brücke (siehe Abb. bei Wurmlöcher). Sie enthält zwei
asymptotisch-flache Räume, die durch einen Schlund (»Wurmloch«) miteinander
verbunden sind. Ein reales Schwarzes Loch entsteht durch Kollaps eines Objektes
(z.B. eines massiven Sterns) auf eine Singularität (siehe Abb. 1, wo durch die
Lage der Lichtkegel zum Ausdruck gebracht wird, dass Signale, die innerhalb des
Ereignishorizontes ausgesandt werden, nie in den Aussenraum gelangen können).
Das von der Oberfläche des kollabierenden Sterns abgestrahlte Licht kommt bei
dem entfernten Beobachter rotverschoben an, wobei die Rotverschiebung durch
![]()
gegeben ist. Die Leuchtkraftabnahme des Sterns beträgt
![]()
so dass der Stern auf der sehr kurzen Zeitskala
![]()
zu erlöschen scheint. Am Horizont wird die Rotverschiebung unendlich. Ein äusserer Beobachter sieht deshalb nie, wie ein Objekt den Ereignishorizont durchdringt.
Da die Einstein-Gleichungen keine Zeitrichtung auszeichnen, ist auch der zu Abb. 1 zeitlich gespiegelte Prozess möglich: die Entstehung eines Sternes aus einem Weissen Loch. Solche Prozesse existieren im Universum vermutlich nicht, was seinen Grund im Zweiten Hauptsatz der Thermodynamik hat (Irreversibilität).
Ersetzt man in der Schwarzschild-Metrik ![]() , so erhält man
die Metrik eines sphärisch-symmetrischen Schwarzen Loches mit elektrischer
Ladung
, so erhält man
die Metrik eines sphärisch-symmetrischen Schwarzen Loches mit elektrischer
Ladung ![]() . Diese
Reissner-Nordström-Lösung ist nur von theoretischer Bedeutung.
. Diese
Reissner-Nordström-Lösung ist nur von theoretischer Bedeutung.
Von realistischen Schwarzen Löchern wird erwartet, dass sie
einen Drehimpuls ![]() besitzen. Die zugehörige Lösung der
Einstein-Gleichungen im Vakuum ist die axialsymmetrische Kerr-Lösung. Durch die
Ersetzung
besitzen. Die zugehörige Lösung der
Einstein-Gleichungen im Vakuum ist die axialsymmetrische Kerr-Lösung. Durch die
Ersetzung ![]() erhält man hieraus die allgemeinste Lösung
eines stationären Schwarzen Loches, welche ein rotierendes elektrisch geladenes
Schwarzes Loch beschreibt. Rotierende Schwarze Löcher sind durch die
Anwesenheit einer Ergosphäre (siehe Abb. 2) gekennzeichnet, einem Bereich
ausserhalb des Ereignishorizontes, in dem es möglich ist, durch bestimmte
Prozesse (Penrose-Prozesse) Energie aus dem Schwarzen Loch (maximal 29 % der
Ruhemasse) zu extrahieren.
erhält man hieraus die allgemeinste Lösung
eines stationären Schwarzen Loches, welche ein rotierendes elektrisch geladenes
Schwarzes Loch beschreibt. Rotierende Schwarze Löcher sind durch die
Anwesenheit einer Ergosphäre (siehe Abb. 2) gekennzeichnet, einem Bereich
ausserhalb des Ereignishorizontes, in dem es möglich ist, durch bestimmte
Prozesse (Penrose-Prozesse) Energie aus dem Schwarzen Loch (maximal 29 % der
Ruhemasse) zu extrahieren.
Schwarze Löcher weisen eine erstaunliche Analogie zu
thermodynamischen Systemen auf. Die Tabelle enthält einen Vergleich der Gesetze
der Mechanik Schwarzer Löcher mit den Hauptsätzen der Thermodynamik. Dabei
bezeichnen ![]() die Oberflächengravitation des Schwarzen
Loches,
die Oberflächengravitation des Schwarzen
Loches, ![]() seine Winkelgeschwindigkeit am Horizont und
seine Winkelgeschwindigkeit am Horizont und ![]() sein elektrostatisches Potential. Stephen
Hawking hat gezeigt, dass die Interpretation dieser zunächst rein formalen
Hauptsätze nur im Rahmen der Quantentheorie geschehen kann. Dabei stellt sich
heraus, dass Schwarze Löcher mit einer Temperatur
sein elektrostatisches Potential. Stephen
Hawking hat gezeigt, dass die Interpretation dieser zunächst rein formalen
Hauptsätze nur im Rahmen der Quantentheorie geschehen kann. Dabei stellt sich
heraus, dass Schwarze Löcher mit einer Temperatur
![]()
strahlen (Hawking-Effekt). Der hierzu analoge Effekt im
flachen Raum ist der Unruh-Effekt: Ein Beobachter, der sich mit einer
Beschleunigung ![]() durch das Vakuum bewegt, beobachtet thermische
Strahlung mit der Temperatur
durch das Vakuum bewegt, beobachtet thermische
Strahlung mit der Temperatur
![]()
Im Falle der Schwarzschild-Metrik lautet die Hawking-Temperatur
![]()
Da das Schwarze Loch mit der Abstrahlung immer heisser wird, verdampft es in endlicher Zeit. Die Lebensdauer ist dabei durch
![]()
gegeben. Über das Endstadium dieser Verdampfung könnte nur
eine (noch ausstehende) Theorie der Quantengravitation Auskunft geben. Für ein
ungeladenes nichtrotierendes Loch mit ![]() beträgt die auf Grund des Hawking-Effektes
ausgestrahlte Leistung
beträgt die auf Grund des Hawking-Effektes
ausgestrahlte Leistung
![]()
wovon 81,4 % in Neutrinos, 16,7 % in Photonen und 1,9 % in
Gravitonen stecken (unter der Annahme, dass sonst keine masselosen Teilchen
existieren). In dem Massebereich ![]() ergibt sich
ergibt sich
![]()
wovon 45 % in Elektronen und Positronen, 45 % in Neutrinos, 9
% in Photonen und 1 % in Gravitonen stecken. Bei kleineren ![]() werden auch massivere Teilchen ausgestrahlt.
Schwarze Löcher unterhalb etwa drei Sonnenmassen können nicht durch
Gravitationskollaps von Sternen entstehen. Sie müssen, falls überhaupt, unter
den extremen Bedingungen des frühen Universums entstanden sein (primordiale
Schwarze Löcher).
werden auch massivere Teilchen ausgestrahlt.
Schwarze Löcher unterhalb etwa drei Sonnenmassen können nicht durch
Gravitationskollaps von Sternen entstehen. Sie müssen, falls überhaupt, unter
den extremen Bedingungen des frühen Universums entstanden sein (primordiale
Schwarze Löcher).
Die Entropie eines Schwarzen Loches ist durch
![]()
gegeben (Bekenstein-Hawking-Entropie), wobei ![]() die Oberfläche des Ereignishorizontes
bezeichnet. (Im Falle der Schwarzschild-Metrik ist
die Oberfläche des Ereignishorizontes
bezeichnet. (Im Falle der Schwarzschild-Metrik ist ![]() .) In
zahlreichen Gedankenexperimenten konnte die Gültigkeit eines verallgemeinerten
Zweiten Hauptsatzes gezeigt werden: Die Summe aus
.) In
zahlreichen Gedankenexperimenten konnte die Gültigkeit eines verallgemeinerten
Zweiten Hauptsatzes gezeigt werden: Die Summe aus ![]() und der Entropie normaler Materie nimmt in
abgeschlossenen Systemen nie ab. Ein offenes Problem ist die Interpretation von
und der Entropie normaler Materie nimmt in
abgeschlossenen Systemen nie ab. Ein offenes Problem ist die Interpretation von
![]() im Rahmen einer mikroskopischen statistischen
Theorie, etwa nach der Gibbs-Formel
im Rahmen einer mikroskopischen statistischen
Theorie, etwa nach der Gibbs-Formel
![]()
wobei ![]() eine geeignete Dichtematrix ist;
eine geeignete Dichtematrix ist; ![]() würde dann die Zahl der Mikrozustände angeben,
die mit dem durch
würde dann die Zahl der Mikrozustände angeben,
die mit dem durch ![]() gegebenen Makrozustand des Loches verträglich
sind. Eine solche Interpretation sollte im Rahmen einer Quantengravitation
möglich sein.
gegebenen Makrozustand des Loches verträglich
sind. Eine solche Interpretation sollte im Rahmen einer Quantengravitation
möglich sein.
Schwarze Löcher von der Masse eines Sterns oder mehr können
auf Grund ihrer Auswirkungen auf ihre Umgebung durch astronomische
Beobachtungen nachgewiesen werden. Beispiele solcher astronomischen Schwarzen
Löcher sind die Röntgenquelle Cygnus X-1 oder das galaktische Zentrum. Bei
Objekten wie Cygnus X-1 befindet sich ein Schwarzes Loch, dessen Masse einige ![]() beträgt, in einem Doppelstern und zieht
Materie des Begleitsterns ab, die sich zunächst in einer Akkretionsscheibe
(Akkretion) anlagert und von dort in das Schwarze Loch beschleunigt wird.
Anhand der Beobachtungen muss ausgeschlossen werden können, dass es sich bei solchen
Objekten um spektroskopische Doppelsterne oder Röntgendoppelsterne handelt.
beträgt, in einem Doppelstern und zieht
Materie des Begleitsterns ab, die sich zunächst in einer Akkretionsscheibe
(Akkretion) anlagert und von dort in das Schwarze Loch beschleunigt wird.
Anhand der Beobachtungen muss ausgeschlossen werden können, dass es sich bei solchen
Objekten um spektroskopische Doppelsterne oder Röntgendoppelsterne handelt.
Schwarze Löcher in den Zentren von Galaxien, sog.
supermassenreiche Schwarze Löcher, besitzen weit höhere Massen von mehr als
einer Million ![]() . Sie wurden
zunächst vorhergesagt, um den hohen Energieausstoss von Quasaren und von aktiven
Galaxien zu erklären. Auch hier geht man davon aus, dass Materie zunächst in
einer Akkretionsscheibe gesammelt und von dort in das Schwarze Loch fällt.
Daneben zwingen diese Schwarzen Löcher das Gas und die Sterne in ihrer Umgebung
dazu, mit hoher Geschwindigkeit um das Massenzentrum zu rotieren, so dass auf
Grund der Rotationsgeschwindigkeit auf die Anwesenheit eines Schwarzen Lochs
geschlossen werden kann. Beispiele solcher Objekte bilden die Radioquelle
Sagittarius A sowie das 1997 mit dem Hubble-Weltraumteleskop entdeckte Schwarze
Loch im Zentrum der Galaxie M84 (siehe Abb. 3).
. Sie wurden
zunächst vorhergesagt, um den hohen Energieausstoss von Quasaren und von aktiven
Galaxien zu erklären. Auch hier geht man davon aus, dass Materie zunächst in
einer Akkretionsscheibe gesammelt und von dort in das Schwarze Loch fällt.
Daneben zwingen diese Schwarzen Löcher das Gas und die Sterne in ihrer Umgebung
dazu, mit hoher Geschwindigkeit um das Massenzentrum zu rotieren, so dass auf
Grund der Rotationsgeschwindigkeit auf die Anwesenheit eines Schwarzen Lochs
geschlossen werden kann. Beispiele solcher Objekte bilden die Radioquelle
Sagittarius A sowie das 1997 mit dem Hubble-Weltraumteleskop entdeckte Schwarze
Loch im Zentrum der Galaxie M84 (siehe Abb. 3).
Supermassive Schwarze Löcher wurden auch postuliert, um die flachen Rotationskurven von Galaxien zu erklären. Demzufolge würden einige Dutzend Schwarze Löcher im Halo von Galaxien genügen, um zusammen mit dem stellaren Gehalt des Halo die hohen Rotationsgeschwindigkeiten in den äusseren Bereichen von Galaxien zu verursachen. Derartige Schwarze Löcher könnten auch mit Kugelsternhaufen gravitativ wechselwirken und im Laufe der Zeit zu deren Auflösung beitragen.
Die Zerstrahlung Schwarzer Löcher lässt sich nur nachweisen, wenn es gelingt, primordiale Löcher zu beobachten, da für Löcher, die aus einem Gravitationskollaps resultieren, die Temperatur zu gering ist. Nachweismöglichkeiten betreffen den Beitrag vieler primordialer Löcher zum diffusen Gammahintergrund sowie die Beobachtung eines einzelnen verdampfenden Loches. Bisher gibt es hierfür nur obere Schranken.
Schwarze Löcher: Vergleich der Gesetze der Mechanik Schwarzer Löcher mit den Hauptsätzen der Thermodynamik.
| bottom:solid gray 1.0pt;border-right:
none;mso-border-top-alt:solid gray .75pt;mso-border-left-alt:solid black .75pt;
mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
Hauptsatz |
bottom:solid gray 1.0pt;border-right:none;mso-border-top-alt:
solid gray .75pt;mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
Thermodynamik |
bottom:solid gray 1.0pt;border-right:solid black 1.0pt;
mso-border-top-alt:solid gray .75pt;mso-border-bottom-alt:solid gray .75pt;
mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
stationäres Schwarzes Loch |
|
Nullter |
T konstant auf einem Körper im
thermischen Gleichgewicht |
|
|
Erster |
|
|
|
Zweiter |
|
|
| bottom:solid gray 1.0pt;border-right:none;mso-border-left-alt:solid black .75pt;
mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
Dritter |
bottom:solid gray 1.0pt;
mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>
|
bottom:solid gray 1.0pt;border-right:solid black 1.0pt;
mso-border-bottom-alt:solid gray .75pt;mso-border-right-alt:solid black .75pt;
padding:0cm 3.55pt 0cm 3.55pt\'>
|
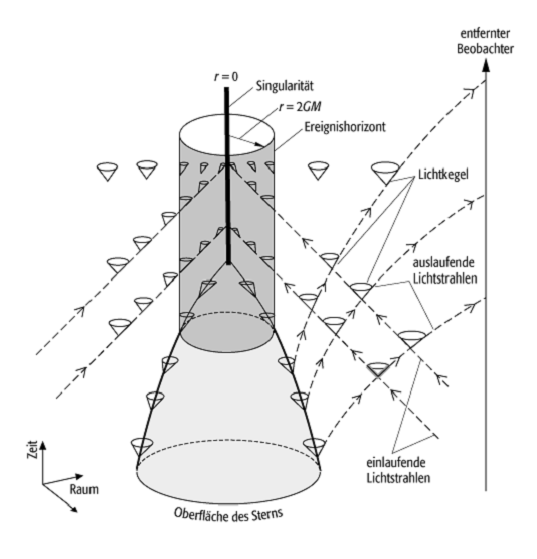
Schwarze Löcher 1: Gravitationskollaps eines Sterns zu einem Schwarzen Loch.
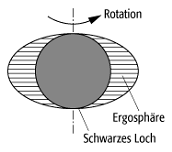
Schwarze Löcher 2: Ergosphäre um ein rotierendes Schwarzes Loch.
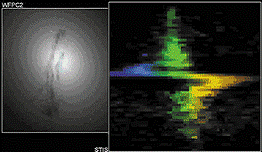
Schwarze Löcher 3: Rotationsgeschwindigkeit im Zentrum der Galaxie M84 hin. Die grossen blau- und rotverschobenen Messwerte (links bzw. rechts) deuten auf die Anwesenheit eines Schwarzen Loches in M84. Ohne Anwesenheit eines solchen Objekts würde man eine in etwa vertikal verlaufende Linie erwarten (Quelle: Hubble Space Telescope, NASA, AURA/ST ScI).


Schwarze Löcher 4: Computersimulation des Einflusses der Raumkrümmung auf ein Gebäude (erstellt an der University of Arizona).
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.