Techniklexikon

Messprozesse in der Quantenmechanik

Quantenmechanik

bottom:.0001pt\'>»Ich bin nicht damit zufrieden, dass man eine Maschinerie hat, die zwar zu prophezeien gestattet, der wir aber keinen klaren Sinn zu geben vermögen.«(Albert Einstein)

bottom:.0001pt\'>Der Begriff der Messung ist seit der Formulierung der Quantentheorie in den zwanziger Jahren ein zentrales und umstrittenes Thema. Er hängt unmittelbar mit dem Problem der Interpretation der Quantentheorie zusammen und damit auch mit der Frage nach der Beziehung zwischen klassischer und Quantenphysik.

bottom:.0001pt\'>In der - in den gängigen Lehrbüchern benutzten - sog. Kopenhagener Interpretation der Quantentheorie wird streng zwischen klassischen Objekten und Quantenobjekten unterschieden. Erstere sind per Postulat in klassischen Begriffen zu beschreiben, während Quantenobjekte durch Wellenfunktionen oder Dichtematrizen (Dichteoperatoren) charakterisiert werden, welche durch geeignete (wiederum klassische) Präparationsvorschriften definiert sind. Dieser Bruch hat sich pragmatisch ausserordentlich bewährt, wie die Erfolge in der Anwendung der Quantentheorie zeigen. Häufig wird die Wellenfunktion daher nicht als Beschreibung realer Objekte, sondern lediglich als Hilfsmittel zur Berechnung von Wahrscheinlichkeiten für Messergebnisse betrachtet.

bottom:.0001pt\'>Diese Situation ist aber aus mehreren Gründen unbefriedigend: Zunächst stellt die (von Bohr und anderen nie klar definierte) Trennung zwischen Mikro- und Makrowelt eine begriffliches Problem dar, das leicht zu Inkonsistenzen führen kann, da makroskopische Objekte aus mikroskopischen aufgebaut sind. Es würde z. B. zu Widersprüchen führen, wenn nicht alle Objekte der Unschärferelation unterlägen. Schliesslich sollte sich der Prozess der Messung (ebenso wie eine Präparation) als Wechselwirkung quantenmechanischer Systeme beschreiben lassen. Das hat von Neumann in seinem Buch (im Gegensatz zu Bohrs Vorstellungen) versucht, wozu er aber die Schrödinger-Dynamik durch den »Kollaps der Wellenfunktion« ergänzen musste (ebenfalls ohne eine genaue Trennline zu definieren). Bohrs pragmatische Einstellung wird zunehmend als unbefriedigend empfunden, vor allem seitdem der Bereich zwischen mikroskopischen und makroskopischen Phänomenen dem Experiment besser zugänglich wird. Aufgrund neuer experimenteller Möglichkeiten erscheint die Grenze zwischen »mikroskopisch« und »makroskopisch« immer mehr verschiebbar.
character:line-break\'>
character:line-break\'>

bottom:.0001pt\'>Phänomenologische Beschreibung

bottom:.0001pt\'>Die übliche Formulierung lautet folgendermassen: Wird die Observable  an einem im Zustand  präparierten System gemessen, so findet man den Eigenwert a_k mit einer Wahrscheinlichkeit |c_k|². Da im Falle reproduzierbarer (»idealer«) Messungen eine unmittelbar nachfolgende Messung dasselbe Resultat liefert, ist der Zustand des Systems nach der Messung nicht mehr , sondern der dem Messwert a_k entsprechende Eigenzustand . Während einer Messung wird daher die unitäre Entwicklung gemäss der Schrödinger-Gleichungdurch einen stochastischen Übergang der Form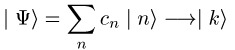

bottom:.0001pt\'>ersetzt. (Für sogenannte »unvollständige« Messungen ist analog eine Projektion auf den entsprechenden Unterraum vorzunehmen.) Diese zweite Dynamik wird meist als Kollaps oder Reduktion der Wellenfunktion bezeichnet; ihre physikalische Bedeutung ist umstritten.

bottom:.0001pt\'>Fasst man die möglichen Endzustände  zu einem Ensemble zusammen, so kann man diesen Prozess auch als Übergang von einem reinen Zustand in ein Gemisch,

bottom:.0001pt\'>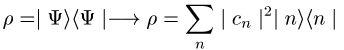

bottom:.0001pt\'>formulieren. Trivialerweise gibt es hier keine Interferenz-(Nichtdiagonal-)Terme zwischen verschiedenen Ergebnissen mehr, da ja im Einzelexperiment immer nur ein Element des Ensembles realisiert ist und die Ergebnisse vieler Einzelexperimente zu addieren sind.

bottom:.0001pt\'>Der Kollaps der Wellenfunktion kann aber nicht als das Herausgreifen eines Elements aus einem Ensemble interpretiert werden, da eine Superposition der Form  Eigenschaften zeigt, die keiner ihrer Komponenten  zukommt. Daher ist der Kollaps ein nicht-triviales dynamisches Axiom und beschreibt nicht, wie oft suggeriert wird, lediglich einen Zuwachs an Information über eine bereits vorliegende Situation.

bottom:.0001pt\'>Die Tatsache, dass die Quantentheorie nur Wahrscheinlichkeitsaussagen liefert, hat zu dem Mythos geführt, es handele sich um eine »statistische« Theorie. Häufig wird auch behauptet, das stochastische Verhalten von Quantenobjekten beruhe auf »Störungen« während der Messung. Dieses Argument würde jedoch eine (in sich konsistente) dynamische Analyse erfordern (s.u.). Dies wurde aber nie gezeigt. Für den Fall, dass sich das System anfangs in einem Eigenzustand zur gemessenen Observablen befindet, bleibt sein Zustand offensichtlich ungestört.

bottom:.0001pt\'>Viele »axiomatische« oder »operationalistische« Zugänge zur Quantentheorie bleiben auf diesem phänomenologischen Niveau stehen, ohne die zugrundeliegenden Begriffe weiter zu analysieren (oder ihre Inkonsistenz zu erkennen). Zum Beispiel wird ein physikalischer »Zustand« häufig durch eine Präparationsvorschrift definiert, obwohl Operationen dieser Art als dynamische Vorgänge beschreibbar sein müssten. Dieser Zustand wird dann als ein formales Ensemble behandelt, ohne die tiefgreifenden Konsequenzen für dessen mögliche Elemente zu prüfen. Ein typisches Beispiel ist der Rückzug auf formale »Erwartungswerte«.
character: line-break\'>
character:line-break\'>

bottom:.0001pt\'>Dynamische Beschreibung

bottom:.0001pt\'>Will man das Geschehen während eines Messprozesses dynamisch verstehen, so erfordert dies eine quantentheoretische Beschreibung sowohl des Messobjekts als auch der (makroskopischen) Messapparatur. Die Grundlage für eine Theorie des Messprozesses wurde bereits durch von Neumann im Jahre 1932 formuliert. Die Mess-Wechselwirkung muss so konstruiert werden, dass sie ein eindeutiges Resultat liefert, falls sich das System anfangs in einem Eigenzustand  der gemessenen Observablen befindet.

bottom:.0001pt\'>Seien die dem Messergebnis n entsprechenden Makrozustände (z. B. beschrieben durch Wellenpakete für einen »Zeiger«), so muss bei einer sog. idealen (d.h. mit demselben Ergebnis wiederholbaren) Messung die Kopplung derart sein, dass die Dynamik durch

bottom:.0001pt\'>

bottom:.0001pt\'>beschrieben wird. Hierbei ist  der (i.a. thermodynamisch metastabile) Anfangszustand des Messgeräts, die  beschreiben die je nach Messergebnis resultierenden Endzustände. Diese sind - da makroskopisch verschieden - immer praktisch orthogonal. Für dieses Schema brauchen weder Anfangs- noch Endzustände des Messapparats im Detail bekannt zu sein. Dynamisch (und realistisch) erforderlich ist lediglich die makroskopische Unterscheidbarkeit der Zeigerstellungen .

bottom:.0001pt\'>Für eine solche (idealisierte) zeitliche Entwicklung geeignete Hamilton-Operatoren haben die Form

bottom:.0001pt\'>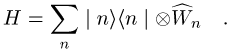

bottom:.0001pt\'>Diese sind immer diagonal in der durch die Zustände  definierten Basis; die Operatoren  bewirken die Änderung des Apparatzustands in Abhängigkeit von n. Umgekehrt wird durch die Angabe der Wechselwirkung schon eine Observable definiert; dieser Begriff ist damit ableitbar (die Eigenwerte einer Observablen entsprechen nur einer Kalibrierung und sind daher eher von sekundärer Bedeutung). Wechselwirkungen dieser Form sind etwa in quantenoptischen Experimenten geradezu »konstruierbar«.
character:line-break\'>
character:line-break\'>

bottom:.0001pt\'>Das Problem des Messprozesses

bottom:.0001pt\'>Der entscheidende Unterschied zur klassischen Physik besteht nun darin, dass die Quantentheorie eine Vielzahl weiterer Objektzustände erlaubt, nämlich Superpositionen verschiedener . Aufgrund der Linearität der Theorie ergibt sich sofort die entsprechende Dynamik für einen allgemeinen Anfangszustand des Objektsystems:

bottom:.0001pt\'>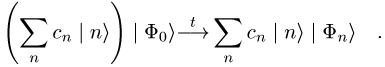

bottom:.0001pt\'>Der resultierende Zustand beschreibt offensichtlich nicht das, was beobachtet wird: Statt einer Komponente  mit Wahrscheinlichkeit  entwickelt sich deterministisch eine Superposition aller möglichen »Resultate«. Diese Diskrepanz wird als das »Problem (oder Paradoxon) des quantenmechanischen Messprozesses« bezeichnet.

bottom:.0001pt\'>Die übliche Antwort auf das Problem besteht in der Behauptung, dass die Wellenfunktion nur Wahrscheinlichkeiten beschreibe. Unabhängig davon, dass meist nicht weiter spezifiziert wird, ob dies Wahrscheinlichkeiten für quantenmechanische Zustände, klassische oder andere (»versteckte«) Grössen sein sollen, besteht der entscheidende Einwand darin, dass sich eine Superposition in allen nachprüfbaren Fällen als verschieden von einem Ensemble seiner Komponenten erweist. Sie definiert völlig neue Eigenschaften. Insbesonders zeigen solche korrelierten (»verschränkten«) Zustände teilweise überraschende Merkmale, wie die Verletzung der Bellschen Ungleichungen. Deswegen hat sich auch Heisenbergs ursprüngliche Vorstellung von lediglich unscharf bestimmbaren klassischen Grössen als unzureichend erwiesen. Ebenso ist das Argument nicht aufrechtzuerhalten, eine Messung bedeute eine »unkontrollierbare Störung« des Systems.

bottom:.0001pt\'>Die makroskopische Natur des Messapparats hilft hier auch nicht weiter. Die mikroskopische Dynamik innerhalb jeder Komponente  mag sehr kompliziert (z.B. ergodisch) sein, trotzdem entsteht notwendigerweise immer ein verschränkter Zustand obiger Form; ein berühmtes Beispiel ist das Schrödingersche Katzen-Experiment.

bottom:.0001pt\'>Die Beschreibung des Objektsystems allein mit Hilfe der Dichtematrix (Dichteoperator), wobei obige Dynamik sich in der Form

bottom:.0001pt\'>

bottom:.0001pt\'>

bottom:.0001pt\'>

bottom:.0001pt\'>darstellt, zeigt ein Verschwinden der Nichtdiagonalelemente, da die Zeigerzustände näherungsweise orthogonal sind. Dies scheint zunächst die phänomenologische Theorie zu bestätigen. Es ist jedoch keine Ableitung des Kollapses der Wellenfunktion, sondern lediglich eine Konsistenzbetrachtung. Eine Ensembleinterpretation dieser Dichtematrix ist unzulässig, da das Objektsystem gar keinen Zustand (Wellenfunktion) besitzt (auch keinen unbekannten). Dichtematrizen für Teilsysteme werden daher auch als uneigentliche Gemische (engl. improper mixtures) bezeichnet. Diese Unterscheidung ist nicht nur formal, sondern hat ihren ganz wesentlichen physikalischen Hintergrund in der Nichtlokalität der Quantenzustände (EPR-Paradoxon, Bellsche Ungleichung).

bottom:.0001pt\'>Für den Messapparat gelten formal analoge Resultate. Wendet man die Wahrscheinlichkeitsregeln auf ihn an, so ergibt sich wie erwartet das Resultat n mit Wahrscheinlichkeit . Dies ist die sog. »Verschiebbarkeit des Schnitts« zwischen Objekt und Beobachter. Aufgrund dieser Freiheit ist es empirisch sehr schwer - wenn nicht unmöglich - zu entscheiden, ob und an welcher Stelle ein Kollaps tatsächlich eintritt. Man darf den Schnitt lediglich nicht zu nahe ans Objekt legen. Solange noch Interferenzen beobachtbar sind, würden Widersprüche auftreten. Auf der anderen Seite kann man ihn beliebig in Richtung zum Beobachter verschieben - im Extremfall in den subjektiven Beobachter selbst, wie u. a. von Neumann oder Wigner vorgeschlagen haben.
character:line-break\'>
character:line-break\'>

bottom:.0001pt\'>Lösungsvorschläge

bottom:.0001pt\'>Die Wege aus diesem Dilemma lassen sich grob in drei Kategorien einteilen. (1) solche, die die quantenmechanische Kinematik verlassen bzw. erweitern, (2) Theorien, welche die Dynamik (die Schrödingergleichung) ändern, und (3) Vorschläge für eine Interpretation der sich formal ergebenden verschränkten »nichtklassischen« Zustände.

bottom:.0001pt\'>Zur Gruppe (1) zählt die Bohm-Theorie, die neben der Wellenfunktion, die sich gemäss der Schrödingergleichung entwickelt (und daher auch alle problematischen Superpositionen enthält), noch Teilchen und ihre Bahnen als wesentliches Element hinzufügt. In dieser Theorie wird angenommen, dass nur die Teilchen für die Beobachtung relevant sind (wahrgenommen werden), während die Wellenfunktion die Rolle eines Führungsfeldes übernimmt. Der Kollaps der Wellenfunktion wird durch eine statistische Annahme über die Verteilung der Teilchen ersetzt. Wie Bell betont hat, ist die Bezeichnung »verborgene Parameter«, die allgemein für Grössen benutzt wird, die die quantenmechanische Beschreibung durch Wellenfunktionen ergänzen sollen, hier irreführend, da ganz im Gegenteil die Wellenfunktion »verborgen« ist.

bottom:.0001pt\'>Von den Theorien der Gruppe (2) ist besonders die von Ghirardi, Rimini und Weber entwickelte Theorie der spontanen Lokalisierung untersucht worden. Diese Versuche ändern die Schrödinger-Gleichung ab (meist durch einen stochastischen Korrekturterm), um einen Kollaps oder äquivalente Effekte zu erhalten, und sind daher im Prinzip experimentell unterscheidbar. Der subjektive Beobachter spielt keine ausgezeichnete Rolle, da die Wahrnehmung als parallel zu Zuständen gewisser Objekte (z.B. Teilen des Gehirns) angenommen werden kann. Ein solcher »psycho-physischer Parallelismus« war ursprünglich für von Neumann auch der Grund, den Kollaps als Ergänzung zur Schrödinger-Dynamik einzuführen. Darauf beruht sicherlich die Attraktivät solcher Modelle.

bottom:.0001pt\'>Allerdings werden die Abweichungen von der Quantenmechanik gerade im interessanten makroskopischen Bereich durch den weiter unten beschriebenen Dekohärenz-Effekt überlagert.

bottom:.0001pt\'>Die dritte Gruppe behält sowohl die Kinematik (also die Wellenfunktion) als auch ihre Dynamik bei. Dazu gehören vor allem die auf Everett zurückgehenden Interpretationen, die manchmal auch als Vielwelten-Theorien bezeichnet werden. In diesen wird als alleinige Dynamik die Schrödingergleichung verwendet. Als Folge entstehen notwendigerweise die obigen Superpositionen makroskopisch verschiedener Zustände. Schrödingers Katze ist also sowohl tot als auch lebendig. Dasselbe gilt auch für jeden Beobachter, der dann notwendigerweise in verschiedenen Versionen (in jeder Komponente der globalen Wellenfunktion) existiert, die sich allerdings nicht gegenseitig wahrnehmen können.
character: line-break\'>
character:line-break\'>

bottom:.0001pt\'>Neuere Entwicklungen

bottom:.0001pt\'>In den letzten Jahrzehnten wurde zunehmend klar, dass das oben beschriebene von Neumannsche Schema eines Messprozesses in einem entscheidenden Punkt unrealistisch ist: Die Beschreibung des Messapparats als isoliertes System, das sich (evtl. in Kopplung an ein Messobjekt) gemäss der Schrödinger-Gleichung entwickelt, entspricht einer Situation, die wir in der realen Welt nie vorfinden. Denn es zeigt sich, dass makroskopische Körper sehr stark mit ihrer natürlichen Umgebung wechselwirken. Dies führt dazu, dass sich in extrem kurzer Zeit ein verschränkter (quantenkorrelierter) Zustand entwickelt, und zwar so, dass Interferenzen zwischen verschiedenen Makrozuständen nicht mehr beobachtbar sind. Dieses Phänomen wird als Dekohärenz bezeichnet.

bottom:.0001pt\'>Zum Beispiel wird der Ort eines makroskopischen Körpers ständig und unvermeidbar durch Streuung von Photonen oder Molekülen »gemessen«, d.h. die Streuzustände enthalten Informationen über den Ort des Objekts. Dies geschieht völlig analog zu der oben beschriebenen unitären Messprozess-Dynamik, weshalb man hier auch von messprozessartigen Wechselwirkungen spricht. Alle makroskopischen Objekte sind daher immer stark mit ihrer Umgebung quantenkorreliert. Quantitative Abschätzungen zeigen, dass diese Nicht-Isolierbarkeit gegenüber der natürlichen Umgebung bis hinein in den Bereich von Molekülen wesentlich ist. In der Tat wird voll quantenmechanisches Verhalten nur bei sehr kleinen Molekülen (wie Wasserstoff oder Ammoniak) beobachtet.

bottom:.0001pt\'>Dekohärenz führt dazu, dass sehr viele Systeme nicht mehr in Superpositionen bestimmter Zustände gefunden werden können (Superauswahlregel). Schrödingers Katze erscheint daher immer entweder tot oder lebendig; der nicht-klassische Superpositionszustand ist dynamisch instabil und äusserst kurzlebig. Die Effekte dieser irreversiblen Kopplung an die Umgebung sind im makroskopischen Bereich sehr viel schneller als thermische Relaxationsprozesse.

bottom:.0001pt\'>Für bestimmte (»klassische«) Freiheitsgrade folgt daher eine effektive Einschränkung des Superpositionsprinzips der Quantentheorie aus der Nichtlokalität von Quantenzuständen (wobei letztere ironischerweise gerade eine Konsequenz des Superpositionsprinzips ist). Solche Superauswahlregeln scheinen also dynamisch begründbar zu sein - im Gegensatz zu Theorien, in denen sie axiomatisch postuliert werden.

bottom:.0001pt\'>Diese realistischen und quantitativen Betrachtungen zeigen, dass klassisches Verhalten (im Sinne von Abwesenheit von Interferenzen) weniger mit der »Grösse« eines Systems zu tun hat, als mit der dynamischen Offenheit der meisten Objekte.

bottom:.0001pt\'>Die Möglichkeit, Dekohärenz-Effekte im mesoskopischen Bereich experimentell zu studieren, erlaubt wichtige Tests der Quantentheorie. Andererseits stellt die Unvermeidbarkeit der Kopplung an die Umgebung ein gewaltiges Hindernis für Konstrukteure von Quanten-Computern dar, da diese eine kontrollierte und dauerhafte Manipulation von (zumindest mesoskopischen) Superpositionen erfordern.

bottom:.0001pt\'>Die starke Kopplung makroskopischer Objekte führt konsequenterweise zur Entwicklung einer Quantenkosmologie. Dies muss auch eine - bisher in Ansätzen vorhandene - Quantentheorie der Gravitation einschliessen. Aus Konsistenzgründen führen solche Betrachtungen notwendigerweise auf das Konzept einer »Wellenfunktion des Universums«. Das Universum enthält aber per definitionem auch alle seine Beobachter. Hier zeigt sich das Interpretationsproblem der Quantentheorie in voller Schärfe.
character:line-break\'>
character:line-break\'>

bottom:.0001pt\'>Literatur:

bottom:.0001pt\'>Von Neumann, J.: Mathematische Grundlagen der Quantenmechanik, Springer, 1932, 1981.
Eine kurz nach der Formulierung der Quantentheorie entstandene Analyse. Heute noch lesenswert ist besonders das Kapitel VI über den Messprozess. Dieses Buch enthält auch den (historisch bedeutsamen, aber leider unbrauchbaren) »Beweis« der Nichterweiterbarkeit der Quantentheorie.
Jammer, M.: The Philosophy of Quantum Mechanics (Wiley), 1974.
Eine Fundgrube zur historischen Entwicklung der Theorie, mit vielen Zitaten und Literaturhinweisen.
Wheeler, J. A. und Zurek, W. H.: Quantum Theory and Measurement, Princeton University Press, 1983.
Eine kommentierte Reproduktion von Beiträgen, die in der Diskussion über die Interpretation der Quantentheorie eine Rolle gespielt haben.
d\'Espagnat, B.: Veiled Reality, Addison-Wesley, 1995.
Eine der gründlichsten Analysen des Problems, was uns die Quantentheorie zu sagen hat.
Giulini, D., Joos, E., Kiefer, C., Kupsch, J., Stamatescu, I.-O. und Zeh, H.D.: Decoherence and the Appearance of a Classical World in Quantum Theory, Springer, 1996.
Diskutiert die neueren Enwicklungen in den Grundlagen der Quantentheorie, mit Betonung auf Interpretationsfragen.