Techniklexikon

Dichtefunktionaltheorie

Atom- und Molekülphysik

bottom:.0001pt\'>1 Einführung

bottom:.0001pt\'>Die Dichtefunktionaltheorie (DFT) [1,2] kann als die exakte Darstellung des quantenmechanischen Vielteilchenproblems durch die Einteilchendichte n(r) bezeichnet werden. Ihre Wurzeln reichen mit der Thomas-Fermi(TF)-Theorie (Thomas-Fermi-Näherung) als der einfachsten Theorie quantenmechanischer Vielteilchensysteme bis in die Anfangszeit der Quantenmechanik zurück. Die TF-Theorie ermöglicht zwar mit relativ wenig Aufwand die Gewinnung formal exakter Ergebnisse, der Vergleich mit den Eigenschaften realer elektronischer Systeme offenbart aber eine Reihe schwerwiegender Defekte der Theorie. So hat die durch direkte Integration der TF-Gleichung erhaltene Dichte n(r) das falsche asymptotische Verhalten für kleine und grosse r, die für die atomaren Elektronendichten charakteristische Schalenstruktur wird nicht erhalten, und vor allem kann die Existenz kondensierter Materie nicht deduziert werden. Erweiterungen der TF-Theorie durch Dirac mit der Berücksichtigung des Austauschs, durch Fermi und Amaldi mit der Korrektur der Selbstwechselwirkung in einer gemittelten Form, durch Weizsäcker mit der Verbesserung der kinetischen Energie über eine Gradientenentwicklung, sowie zahlreiche, meist phänomenologische Modifikationen zeigten in quantitativer Hinsicht nur bescheidene Erfolge. Die Einsicht, dass viele Defekte der TF-Theorie in der schlechten Darstellung der kinetischen Energie begründet sind, führte 1951 zuerst Slater zur Formulierung eines Ansatzes, in dem die kinetische Energie entsprechend der Hartree-Fock(HF)-Theorie (Hartree-Fock-Näherung) mit Hilfe von Wellenfunktionen berechnet, der Austausch aber entsprechend der TF-Theorie über alle besetzten Zustände gemittelt wurde. Die Verallgemeinerung dieses Ansatzes zur sog. Xa-Näherung lieferte mit der Hartree-Fock-Slater(HFS)-Theorie (Hartree-Fock-Slater-Näherung) den Rahmen für eine ganze Klasse von Methoden zur Berechnung der elektronischen Struktur von Molekülen und Festkörpern [3]. Deren praktische Erfolge in den siebziger und frühen achtziger Jahren wurden in Anbetracht der relativen Einfachheit dieses theoretischen Schemas allgemein als überraschend, wenn nicht gar als reiner Zufall angesehen. Dass die guten Ergebnisse der HFS-Theorie kein Zufall sind und auch die TF-Theorie keine fiktive, für praktische Zwecke irrelevante Modelltheorie darstellt, zeigt die Integration beider Ansätze in die DFT; die DFT kann insofern als die exakte, quantenmechanische Erweiterung der TF-Theorie angesehen werden.

bottom:.0001pt\'>Die zentrale Aussage der DFT, dass die Grundzustandseigenschaften eines quantenmechanischen Vielteilchensystems allein durch seine Einteilchendichte n(r) eindeutig und vollständig bestimmt sind, ist durchaus bemerkenswert und keineswegs selbstverständlich, insbesondere vor dem Hintergrund "konventioneller" Darstellungen des quantenmechanischen Vielteilchenproblems. Darunter sind alle Darstellungen zu verstehen, deren zentrale Grösse die Vielteilchenwellenfunktion Y ist. In diesem Rahmen können die Vielteilcheneffekte mit Hilfe der Paardichte (Korrelation) beschrieben werden, die symbolisch in der Form  darstellbar ist, wobei  die Paarkorrelationsfunktion bezeichnet. In HF-Näherung ist  entsprechend dem Modell unabhängiger Teilchen, während etwa die Entwicklung von Y nach Slater-Determinanten dazu führt, dass die Paardichte nicht mehr faktorisierbar ist. Insofern kann man sagen, dass in der konventionellen Darstellung des Vielteilchenproblems alle Vielteilcheneffekte in der Paardichte enthalten sind. Es ist verständlich, dass vor diesem Hintergrund jede Theorie, die mit der Einteilchendichte auszukommen behauptet, als nicht exakt erscheinen muss; dass dies nicht der Fall ist, gehört zu den grundlegenden Ergebnissen der DFT.

bottom:.0001pt\'> 

bottom:.0001pt\'>2 Der theoretische Rahmen

bottom:.0001pt\'>2.1 Die Hohenberg-Kohn-Theoreme

bottom:.0001pt\'>Als Geburtsjahr der DFT kann das Jahr 1964 gelten, in dem mit einer Arbeit von Hohenberg und Kohn [4] die theoretische Basis und der konzeptionelle Rahmen dieser Theorie in Form einer Reihe von Sätzen begründet wurde, die heute den Namen Hohenberg-Kohn(HK)-Theoreme tragen. Um deren Bedeutung und Tragweite verständlich zu machen, sei daran erinnert, dass in der konventionellen Behandlung des N-Elektronenproblems das von der Kernanordnung erzeugte "externe" Potential  v _ext(r) zusammen mit der Elektronenzahl N den Hamilton-Operator und damit im Prinzip alle Eigenschaften des Grundzustands eindeutig festlegt. Das erste HK-Theorem besagt nun in seiner ursprünglichen Formulierung, dass im Fall eines nichtentarteten Grundzustands statt N und  v _ext(r) auch die Einteilchendichte n(r) dies leistet:

bottom:.0001pt\'>(HK1) Das externe Potential  v _ext(r) eines N-Elektronensystems ist bis auf eine physikalisch bedeutungslose Konstante eindeutig durch die Einteilchendichte n(r) bestimmt. Die Energie E₀ des Grundzustands ist ein eindeutiges Funktional dieser Dichte, d.h. E₀ = E[n].

bottom:.0001pt\'>Da die Einteilchendichte n(r) über die Normierungsbedingung  die Zahl der Elektronen festlegt, bestimmt sie im Prinzip auch die Wellenfunktion des Grundzustands. Ferner ist das externe Potential  v _ext(r) nicht auf Coulomb-Potentiale beschränkt; es muss lediglich lokal sein und kann daher auch entsprechende von aussen angelegte elektrische Felder einschliessen. Der Beweis dieses Theorems ist erstaunlich einfach und beruht auf reductio ad absurdum: es werden zwei wesentlich, d.h. um mehr als eine Konstante verschiedene, externe Potentiale angenommen, die zu derselben Grundzustandsdichte gehören sollen; anschliessend wird gezeigt, dass diese Annahme auf einen Widerspruch führt. Es besteht daher ein umkehrbar eindeutiger Zusammenhang zwischen n(r) und  v _ext(r). Darüber hinaus gilt für die Einelektronendichte ein Variationsprinzip, in dem die Grundzustandsdichte das Funktional E[n] der Gesamtenergie stationär macht:

bottom:.0001pt\'>(HK2) Gegeben sei eine Elektronendichte n ¢ (r), die die Bedingungen n ¢ (r) ³ 0 (für alle r) und  erfülle. Dann ist die damit berechnete Energie immer grösser als die exakte Grundzustandsenergie E₀, d.h. E[n ¢ ] ³ E₀, und das Gleichheitszeichen gilt genau dann, wenn n ¢ (r) gleich der exakten Einteilchendichte n(r) des Grundzustands ist.

bottom:.0001pt\'>Ist ausserdem E[n] differenzierbar, lässt sich unter der Nebenbedingung fester Teilchenzahl N die Euler-Lagrange-Gleichung

bottom:.0001pt\'>  (1)

bottom:.0001pt\'>herleiten, wobei der Lagrange-Parameter m als chemisches Potential interpretiert werden kann. Die Existenz des Funktionals E[n] ist dabei aufgrund von (HK1) zwar gesichert, über dessen konkrete Form gibt das Theorem aber keine Auskunft.

bottom:.0001pt\'>Einen ersten Schritt in diese Richtung stellt das dritte HK-Theorem dar:

bottom:.0001pt\'>(HK3) Die Gesamtenergie eines N-Elektronensystems in einem lokalen, externen Potential  v _ext(r) kann dargestellt werden in der Form

bottom:.0001pt\'>  (2)

bottom:.0001pt\'>mit einem von  v _ext(r) unabhängigen und in diesem Sinn universellen Funktional F_HK[n], das sich aus der kinetischen Energie T[n] der Elektronen und der Elektron-Elektron-Wechselwirkung V_ee[n] zusammensetzt.

bottom:.0001pt\'>In Bezug auf seine n-Abhängigkeit hat demnach F_HK[n] in allen Systemen dieselbe Form, so dass das N-Elektronenproblem in einen allgemeinen, systemunabhängigen und in einen systemspezifischen Teil zerlegt werden kann. Der allgemeine Teil des Problems hat die Frage zu klären, in welcher Form F_HK von n(r) abhängt, während der systemspezifische Teil ausschliesslich durch die spezielle Form von n(r) bestimmt ist: beim Übergang von einem elektronischen System zu einem anderen ändert sich folglich nur n(r), nicht dagegen die funktionale Form von F_HK. Diese Zerlegung der Gesamtenergie ist von fundamentaler Bedeutung, da sie im Prinzip die Behandlung des N-Elektronenproblems unabhängig von Annahmen über spezielle Systeme ermöglicht.

bottom:.0001pt\'> 

bottom:.0001pt\'>2.2 Die Kohn-Sham-Darstellung

bottom:.0001pt\'>Über die konkrete Form von F_HK als Funktional von n(r) wird in den Hohenberg-Kohn-Theoremen keine Aussage gemacht. Die Bestimmung dieses Funktionals ist eine der zentralen Aufgaben der DFT, weil dies nicht nur die notwendige Voraussetzung für praktische Anwendungen schafft, sondern gleichbedeutend mit der Lösung des Vielteilchenproblems ist. Die grösste Schwierigkeit stellt dabei die kinetische Energie T[n] dar, weil sie einen grossen Beitrag zur Gesamtenergie liefert und deswegen sehr genau berechnet werden muss. Da eine direkte Berechnung, wie sie im Rahmen der TF-Theorie versucht wird, zu schlechte Ergebnisse liefert, um für praktisch relevante Anwendungen konkurrenzfähig zu sein, schlugen Kohn und Sham [5] einen Lösungsansatz vor, der heute die Basis der meisten numerischen Rechnungen im Rahmen der DFT bildet. Die Grundidee dieser Kohn-Sham(KS)-Darstellung besteht darin, die kinetische Energie T₀[n] des wechselwirkungsfreien N-Elektronensystems, die den bei weitem grössten Beitrag zur kinetischen Energie liefert, in exakter Form darzustellen und die verbleibende kleine Korrektur T_c[n] getrennt zu behandeln. Die Anwendung des Variationsprinzips führt dann auf eine Euler-Lagrange-Gleichung der Form

bottom:.0001pt\'>  (3)

bottom:.0001pt\'>wobei das lokale, effektive Potential

bottom:.0001pt\'>  (4)

bottom:.0001pt\'>als einzigen, nicht exakt bestimmbaren Beitrag das Austauschkorrelationspotential  v _xc[n(r)] (Austauschkorrelationsenergie) enthält. Diese Darstellung des quantenmechanischen Vielteilchenproblems hat die Struktur eines Problems unabhängiger Teilchen, ist aber unverändert exakt. Auch damit ist allerdings die direkte Lösung von Gleichung (3) nicht möglich, weil die explizite Form von T₀[n] als Funktional von n(r) bisher nicht bekannt ist. Geht man aber zur Orbitaldarstellung der kinetischen Energie T₀[n] über und führt die Variation nach den Orbitalen statt nach der Dichte durch, erhält man die kanonische Form der Kohn-Sham(KS)-Gleichungen in Orbitaldarstellung:

bottom:.0001pt\'>

bottom:.0001pt\'>Diese Gleichungen sind nichtlinear und müssen iterativ gelöst werden, wobei die Selbstkonsistenz zwischen der Einteilchendichte n(r) und  v _eff(r), Gleichung (4), zu erreichen ist. Sie haben unverändert die Struktur von Einteilchengleichungen, sind aber nichtsdestoweniger eine exakte Darstellung des N-Elektronenproblems, wobei alle Vielteilcheneffekte in  v _xc[n(r)] enthalten sind. Als der entscheidende Vorteil der KS-Darstellung im Vergleich zur direkten Berechnung von T[n] erweist sich dabei, dass der Übergang zur Orbitaldarstellung die zwar indirekte, aber exakte Behandlung des grössten Teils T₀ der kinetischen Energie ermöglicht. Dadurch werden nämlich die wesentlichen Defekte der TF-Theorie, wie das falsche asymptotische Verhalten von n(r), das Fehlen der Schalenstruktur bei Atomen sowie der chemischen Bindung in Molekülen und Festkörpern, beseitigt. Der Preis, den man für diese Verbesserung zu zahlen hat, ist allerdings, dass nun N Gleichungen für y_i(r) zu lösen sind statt einer einzigen für n(r). Dennoch bleibt der Aufwand für die Lösung der KS-Gleichungen vergleichbar mit dem des quasiklassischen Hartree-Problems.

bottom:.0001pt\'> 

bottom:.0001pt\'>2.3 Dichtefunktionaltheorie im Vergleich zur Wellenfunktionstheorie

bottom:.0001pt\'>Zusammenfassend lässt sich feststellen, dass die DFT eine Darstellung des quantenmechanischen N-Elektronenproblems liefert, die in gewisser Weise reziprok zu den konventionellen Ansätzen der Wellenfunktionstheorie (WFT) ist, in symbolischer Darstellung:

bottom:.0001pt\'>.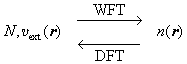

bottom:.0001pt\'>Zentrale Grösse der DFT ist die Einteilchendichte n(r) des Grundzustands, die im Gegensatz zur abstrakten Vielteilchenwellenfunktion Y eine Observable und als Funktion im dreidimensionalen Ortsraum leicht interpretierbar ist. Der Hamilton-Operator des N-Elektronensystems wird in der KS-Darstellung der DFT in ein lokales Funktional der Einteilchendichte transformiert und hat dadurch die Struktur eines Einteilchenoperators. Die HF-Gleichungen enthalten dagegen mit dem HF-Austauschpotential einen wesentlichen nichtlokalen Term und sind daher nicht als Spezialfall der KS-Gleichungen rekonstruierbar. Als System von Einteilchen-Gleichungen sind die KS-Gleichungen numerisch relativ leicht zu lösen, bilden aber unverändert eine exakte Darstellung des N-Elektronenproblems. Dass dies kein Widerspruch ist, hat seinen Grund darin, dass empirisch signifikant nur der Erwartungswert  ist, nicht dagegen y oder H allein. Es spielt daher keine Rolle, ob die Vielteilcheneffekte wie in der WFT über y berücksichtigt werden, oder wie in der DFT über den Hamilton-Operator H, der in Form des Austauschkorrelationsfunktionals sämtliche Vielteilcheneffekte enthält. Neben dessen Berechnung, die eine der zentralen Aufgaben darstellt, umfasst die aktuelle Forschung innerhalb der DFT die Untersuchung von Grundlagenproblemen mit dem Ziel einer Verbesserung der theoretischen Basis, Erweiterungen der Theorie etwa auf die Beschreibung angeregter Zustände bis hin zu der von nichtelektronischen Systemen, sowie die praktischen Anwendungen in Form der Berechnung von n(r) für reale Systeme wie Atome, Moleküle und Festkörper.

bottom:.0001pt\'> 

bottom:.0001pt\'>2.4 Theorieerweiterungen

bottom:.0001pt\'>In ihrer ursprünglichen Formulierung bezieht sich die DFT auf den Grundzustand eines N-Elektronensystems in einem zeitunabhängigen, lokalen, externen Potential ohne Berücksichtigung magnetischer und relativistischer Effekte. Mittlerweile existieren jedoch eine ganze Reihe von Erweiterungen dieses "Theoriekerns", wie eine zeitabhängige und eine relativistische DFT, eine DFT der Supraleitung sowie Formulierungen für mehrkomponentige und nichtelektronische Systeme.

bottom:.0001pt\'>Die für praktische Anwendungen besonders wichtige Erweiterung der KS-Gleichungen auf Systeme mit offenen Schalen ist im Rahmen einer nichtrelativistischen Beschreibung leicht möglich. Enthält der Hamilton-Operator keine spinabhängigen Wechselwirkungen und exterene Magnetfelder, kann man ganz analog zum spinfreien Fall ein System von spinabhängigen ("spin-polarisierten") KS-Gleichungen getrennt für  und  herleiten. Die daraus resultierende Erweiterung wird als Spindichtefunktionaltheorie (SDFT) bezeichnet. Eine andere wichtige Erweiterung der DFT betrifft die elektronisch angeregten Zustände. Für die allgemeine Lösung dieses Problems existiert zwar eine Reihe von Ansätzen [1, 2], insgesamt muss man jedoch sagen, dass eine formal befriedigende und gleichzeitig praktisch nutzbare Beschreibung angeregter Zustände bisher nicht existiert, obwohl im pragmatischen Sinn die DFT in der Regel für die Berechnung mindestens der niedrigsten angeregten Zustände funktioniert.

bottom:.0001pt\'> 

bottom:.0001pt\'>2.5 Konstruktion von Funktionalen

bottom:.0001pt\'>Die Austauschkorrelationsenergie E_xc ist in der KS-Darstellung definiert als Differenz zwischen der exakten Grundzustandsenergie und denjenigen Anteilen, die exakt berechenbar sind. Eine exakte analytische Darstellung auch des Austauschkorrelationsfunktionals E_xc[n] kann dagegen nicht erwartet werden, denn das würde ja bedeuten, dass das quantenmechanische N-Elektronenproblem analytisch lösbar wäre. Da eine solche Lösung nicht einmal für das freie oder homogene Elektronengas als dem einfachsten elektronischen System existiert, muss man zwangsläufig auf Näherungen zurückgreifen. Die einfachste ist die sog. Lokale-Dichte- bzw. die Lokale-Spin-Dichte (LSD)-Näherung, in deren Rahmen die Austauschkorrelationsenergie eines beliebigen, inhomogenen Systems lokal, d.h. in einem infinitesimal kleinen Volumen d³r wie die eines homogenen Systems angenommen wird. Trotz ihrer zahlreichen Erfolge [3, 6] enthält die LSD-Näherung eine Reihe charakteristischer Schwächen, die zu einem grossen Teil auf die unzureichende Darstellung des Austauschbeitrages zu E_xc[n] zurückzuführen sind. Die meisten dieser Defekte lassen sich jedoch durch Austauschkorrelationfunktionale beseitigen, die Gradientenkorrekturen erster Ordnung in n(r) einschliessen (Gradienten-Näherung). Damit konnten in den letzten Jahren grosse Fortschritte, insbesondere bei der Berechnung von Bindungsenergien und damit der thermochemischen Charakterisierung von Molekülen erzielt werden [7]. Ein grosses Problem stellen dagegen nach wie vor die stark korrelierten Systeme dar, was insofern verständlich ist, als die gradientenkorrigierten Funktionale von einer Verbesserung der LSD-Näherung ausgehen. Fortschritte in diesem Bereich dürften deswegen eher von einem alternativen Ansatz zu erwarten sein, bei dem Austauschkorrelationsfunktionale ausgehend von der Dichte-Matrix-Darstellung der WFT konstruiert werden.

bottom:.0001pt\'> 

bottom:.0001pt\'>3 Anwendungen

bottom:.0001pt\'>Der ursprüngliche Anwendungsbereich numerischer DFT-Methoden, wenn man von Anwendungen der TF-Theorie absieht, ist die Festkörperphysik. Die ersten Bandstrukturrechnungen mit dem Slaterschen Austauschpotential (Hartree-Fock-Slater-Näherung) datieren aus den fünfziger Jahren, und heute erfolgen schätzungsweise mehr als 90 % aller Berechnungen der elektronischen Struktur von Festkörpern, Oberflächen und dünnen Schichten im Rahmen der DFT. Während bis etwa Anfang der achtziger Jahre überwiegend die Lokale-Dichte-Näherung verwendet wurde, gehören heute Rechnungen mit gradientenkorrigierten Funktionalen zum Standard. Erste Rechnungen an Molekülen sind erst Ende der sechziger Jahre versucht worden, und bis Mitte der achtziger Jahre stellten die DF-Methoden eher eine Randerscheinung innerhalb der traditionellen Quantenchemie dar. Die bis dahin durchweg verwendeten LSD-Methoden lieferten zwar recht gute Ergebnisse für die elektronische Struktur und zahlreiche spektroskopische Daten, ergaben aber erheblich zu grosse Bindungsenergien und waren damit für die thermochemische Charakterisierung von Molekülen nicht geeignet. Dies änderte sich erst mit dem Einsatz gradientenkorrigierter oder noch allgemeinerer ("nichtlokaler") Austauschkorrelationsfunktionale; seither zählen die DF-Methoden auch in der Quantenchemie zu den am meisten verwendeten Verfahren. Aus diesen Gründen ist eine repräsentative Beschreibung der numerischen Anwendungen der DFT in der Atom-, Molekül- und Festkörperphysik mit wenigen Sätzen nicht mehr möglich. Im grossen und ganzen kann man jedoch sagen, dass die Berechnung messbarer Grössen wie Geometrien, Dipolmomente, Ionisierungspotentiale, Bindungsenergien, Schwingungsfrequenzen und Hyperfein-Parameter bereits in LSD-Näherung oftmals bessere Ergebnisse liefert als die HF-Näherung, während mit den gegenwärtig zur Verfügung stehenden nichtlokalen Funktionalen in den meisten Fällen eine mit den besten Vielteilchenrechnungen vergleichbare Güte erreicht werden kann. Die Vorteile der DF-Methoden werden besonders deutlich bei den Verbindungen der Übergangsmetalle, bei denen HF-Methoden häufig qualitativ falsche Resultate liefern und die Anwendung von Vielteilchenmethoden sehr aufwendig ist, sowie bei der Behandlung grosser Systeme wie biologischer Moleküle. Schliesslich sind die in letzter Zeit stark zunehmenden Untersuchungen zur Charakterisierung chemischer Reaktionen zu erwähnen, sowie die erfolgreiche Kombination von DF-Methoden mit der Moleküldynamik zur Bestimmung von Strukturen kleiner Cluster [6]. Bei allen diesen Erfolgen sollte jedoch nicht übersehen werden, dass die DFT noch weit davon entfernt ist, das Allheilmittel für die Bewältigung sämtlicher Probleme der Elektronentheorie von Atomen, Molekülen, Clustern und Festkörpern zu sein.

bottom:.0001pt\'> 

bottom:.0001pt\'>4 Zusammenfassung

bottom:.0001pt\'>Die DFT liefert eine formal exakte Darstellung des quantenmechanischen Vielteilchenproblems, die in gewisser Weise komplementär zu den traditionellen Methoden der Wellenfunktionstheorie (WFT) ist. Die Entwicklungen der letzten 30 Jahre haben dabei gezeigt, dass in dieser Umformulierung des Vielteilchenproblems sowohl in praktischer als auch in konzeptioneller Hinsicht ein enormes Potential liegt. Denn die Existenz einer exakten Theorie, in der die Einteilchendichte die Schlüsselrolle spielt, die im Gegensatz zur Vielteilchenwellenfunktion observabel und leicht interpretierbar ist, liefert nicht nur eine ganze Familie effizienter Berechnungsverfahren, sondern vor allem einen begrifflichen Rahmen, der den empirischen Begriffssystemen der Physik und Chemie wesentlich angepasster ist als das abstraktere Begriffssystem der WFT. Die Popularität und Verbreitung der DFT bei der Untersuchung von Elektronenstrukturproblemen dürfte aus diesen Gründen auch in der Zukunft weiter zunehmen.

Literatur
[1] R.G. Parr, W. Yang: Density-Functional Theory of Atoms and Molecules, Oxford University Press, Oxford 1989.
[2] R.M. Dreizler, E.K.U. Gross: Density Functional Theory; Springer, Heidelberg-New York 1990.
[3] J.P. Dahl, J. Avery (Eds.): Local Density Approximations in Quantum Chemistry and Solid State Physics, Plenum Press, New York-London, 1984.
[4] P. Hohenberg, W. Kohn, Phys. Rev. 136 (1964) B864-871.
[5] W. Kohn, L.J. Sham, Phys. Rev. 140 (1965) A1133-1138.
[6] R.O. Jones, O. Gunnarsson, Rev. Mod. Phys. 61(1989) 689-746.
[7] R.F. Nalewajski (Hrsg.), Density Functional Theory I; Top. Curr. Chem. 180, Springer 1996.