Techniklexikon

numerische Integration

Mathematische Methoden und Computereinsatz, die Aufgabe, Integrale oder die Lösung von Differentialgleichungssystemen numerisch zu berechnen. Das Gebiet der numerischen Integration gehört zu den wichtigsten der numerischen Mathematik und den angewandten Wissenschaften. Die verwendeten Verfahren, von denen viele in Programmbibliotheken oder numerischer Software enthalten sind, für die verschiedenen Integrationsprobleme (ein- und mehrdimensionale Integrale, gewöhnliche, differentiell-algebraische oder partielle Differentialgleichungen) unterscheiden sich erheblich in ihrer Methodik und Konzeption.

1a) Der einfachste Fall ist die Auswertung des Integrals  für eine auf dem Intervall  stetige und reellwertige Funktion . Dabei wird  durch die Quadraturformel

mit geeigneten Stützstellen  und von  unabhängigen Gewichten  approximiert, wobei man zu vorgegebenem Fehler  die Approximation , d.h. ein Konstruktionsverfahren zur Bestimmung von  und  so bestimmen möchte, dass für eine möglichst grosse Klasse von stetigen Funktionen  erfüllt ist. Hierzu bieten sich interpolierende Quadraturformeln an, die  durch Interpolation von  durch Grundfunktionen  einer bestimmten Funktionenklasse  (z.B. Polynome) berechnen und auf  exakt sind, d.h. für alle  gilt . Die Newton-Cotes Formeln sind ein Beispiel für eine interpolierende Quadraturformel, die auf einem System äquidistanter Stützstellen aufbaut. Basiert eine interpolierende Quadraturformel auf einer Schrittweitenfolge , die gegen Null konvergiert (Beispiel: sukzessive Intervallhalbierung  mit ), so kann unter bestimmten Voraussetzungen die Folge  extrapoliert, d.h. konvergenzbeschleunigt werden. Ein Beispiel hierfür ist das Romberg-Verfahren, das aus einer Extrapolation der  Trapezregel mit Hilfe des Neville-Algorithmus hervorgeht. Für Funktionen, die in einigen Bereichen des Intervalls  eine starke, in anderen jedoch nur wenig Krümmung aufweisen, bieten sich adaptive Verfahren an, die automatisch die Stützstellen im Integrationsintervall so wählen, dass der Integrationsfehler klein wird und sich somit dem Integranden anpassen.

Ein weiteres Verfahren, nämlich das Gausssche Integrationsverfahren, (Gauss-Quadratur) erhält man durch die Betrachtung der Integrale , wobei  eine auf  positive und stetige Funktion ist und  wieder durch  approximiert werden soll. Allerdings wird nun auf die äquidistante Verteilung der Stützstellen  verzichtet, und sowohl die Gewichte  als auch  dürfen frei gewählt werden, wobei eine exakte Integration von Polynomen bis zum Grade  erzielt wird, wenn man die Stützstellen  als Nullstellen der mit Hilfe des Skalarproduktes

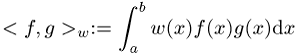
und z.B. des Gram-Schmidtschen Orthogonalisierungsverfahrens erzeugten orthogonalen Polynome  wählt. Die Gewichte  berechnen sich aus der Vorschrift

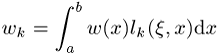
wobei  die Nullstellen des -ten Orthogonalpolynoms bezeichnet (es lässt sich zeigen, dass diese Nullstellen sämtlich reell, einfach und in  gelegen sind) und  das Lagrangesche Fundamentalpolynom zu den  als Stützstellen ist. In praktischen Anwendungen werden je nach Intervall  und Gewichtsfunktionen  die Legendre- (), Tschebyschew- (), Laguerre- () oder Hermite-Polynome  verwendet (siehe Tabelle).

Bei festem  und gleichem Rechenaufwand ist die Gauss-Integration genauer als die interpolierenden Quadraturformeln. Allerdings verliert man beim Übergang von  nach  sämtliche bereits ausgewerteten Funktionswerte; an dieser Stelle erweisen sich Extrapolationsverfahren als vorteilhafter.

Manchmal kann es auch nützlich sein, wenn ein leistungsstarker Integrator für gewöhnliche Differentialgleichungen verfügbar ist, das Integral  mit Hilfe der Differentialgleichung

und der Anfangsbedingung  und  zu berechnen. Schliesslich seien noch Monte-Carlo-Methoden als Integrationsverfahren erwähnt.

1b) Mehrdimensionale Integrale

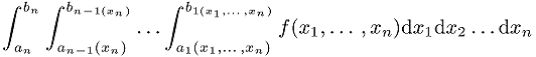
wird man, insbesondere wenn einfache Integrationsgrenzen oder Randdarstellungen dies zulassen, versuchen, auf eindimensionale Integrale zurückzuführen, um dann die oben erwähnten Verfahren anzuwenden. Gelingt dies nicht, so wird man eine zu eindimensionalen Integralen analoge Darstellung

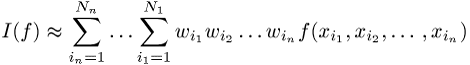
mit geeigneten Gewichten  und Stützstellen  wählen; ist insbesondere der Rand eine schwierige Funktion, so kommen Monte-Carlo-Methoden zum Einsatz.

1c) Die Auswertung von Integralen  auf endlichen Intervallen, bei denen  oszillatorisches Verhalten zeigt - derartige Integrale treten im Zusammenhang mit Fourier-Reihen auf - erfolgt mit Hilfe von Tschebyschew-Interpolationspolynomen, Tschebyschew-Entwicklungen und der Verwendung von Bessel-Funktionen.

1d) Die numerische Integration experimentieller Daten, die möglicherweise noch irregulär verteilt sind, führt man am besten durch, in dem man die Messdaten mit Hilfe von spline-Funktionen interpoliert und diese dann integriert.

2a) Numerische Methoden zur Integration gewöhnlicher Differentialgleichungssysteme, die als Anfangswertprobleme

vorliegen, lassen sich in vier Klassen unterteilen: Einschrittverfahren (Beispiel: Runge-Kutta-Methoden), Mehrschrittverfahren (Beispiele: Adams-Bashforth-Verfahren, Adams-Moulton-Verfahren), Prädiktor-Korrektor-Methoden und Extrapolationsverfahren (Bulirsch-Stoer-Verfahren). Das Polygonzug-Verfahren von Euler (Euler-Cauchy-Verfahren), hergeleitet aus der Taylor-Reihenentwicklung

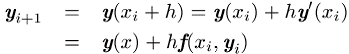
zeigt die Idee eines expliziten Einschrittverfahrens : das Verfahren ist rekursiv und ein weiterer Wert  lässt sich allein aus seinem Vorgänger  (und natürlich ,  und ) berechnen. Würde  auch von  abhängen, so läge ein implizites Einschrittverfahren vor. Ein allgemeines -Schrittverfahren lässt sich mit  dagegen in der Form

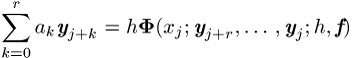
schreiben; zu beachten ist, dass ein Schrittverfahren mit  Startwerten initialisiert werden muss, die man z.B. mit Hilfe eines Einschrittverfahrens berechnen kann.

2b) Numerische Methoden zur Integration impliziter Differentialgleichungen  oder differential-algebraischer Systeme

mit konsistenten Anfangsbedingungen  und  lassen sich durch den Index charakterisieren und als Differentialgleichungen auf Mannigfaltigkeiten interpretieren; dies erlaubt eine Kombination von Integrationsverfahren gewöhnlicher Differentialgleichungen und nichtlinearen Gleichungslösern mit Homotopietechniken. Das Problem (*) hat Index 1, wenn die Matrix  regulär ist. Derartige Probleme treten in der chemischen Verfahrenstechnik oder Elektrotechnik auf; in der Mehrkörpermechanik und Robotik liegt meist ein Index-3-Problem vor. Die algebraische Gleichung  wird mit Hilfe des im Grenzwert gegen 0 strebenden Homotopieparameters  in die Differentialgleichung

eingebettet.

2c) Numerische Methoden zur Integration gewöhnlicher Differentialgleichungssysteme, die als Randwertprobleme

mit  auf einem Intervall  vorliegen, lassen sich in vier Klassen unterteilen: Einschiessverfahren, Mehrzielmethode, Differenzenverfahren und Variationsverfahren (Ritz-Galerkin-Verfahren). Liegen die Randwertbedingungen bei einem Differentialgleichungssystem zweiter Ordnung  in Form zweier separierter, expliziter Randbedingungen vor, z.B.  und , so besteht das intuitiv einleuchtende, aber, je nach Problem, numerisch nicht sehr stabile Einschiessverfahren darin, von  ausgehend ein Anfangswertproblem zu lösen, wobei die unbekannte Anfangssteigung  dazu verwendet wird, auf die Bedingung  zu zielen und diese, z.B. mit Hilfe des Newton-Verfahrens zu erfüllen. Allgemeiner ist der Fall, dass für die beiden Intervallgrenzen jeweils einige, aber weniger als  Bedingungen zu erfüllen sind. Diesen Fall trifft man z.B. bei den den Sternaufbau beschreibenden Differentialgleichungen, deren unabhängige Variable  die Masse  ist, an; einige Grössen, z.B. die Temperatur, sind an der Sternoberfläche bekannt, andere, wie Radius und Leuchtkraft, im Zentrum () des Sterns, wo sie den Wert 0 annehmen. In der Mehrzielmethode verwendet man ein an das Problem angepasstes Gitter  von  Stützstellen  ( Teilintervalle ),

welches das Intervall  überdeckt und die Punkte  enthält, und die diskrete Trajektorie  wird als Variable eingeführt; die  sind dabei die Anfangswerte der Teiltrajektorien. Integriert wird dabei jeweils von  bis . Zu einer gegebenen Schätzung des Variablenvektors  berechnet man die Lösungen  der  unabhängigen Anfangswertprobleme auf jedem Teilintervall  und erhält so eine (zunächst unstetige) Parameterisierung von . Durch die zusätzlichen Anschlussbedingungen  wird die Stetigkeit der Lösung gesichert. Zusammen mit den ursprünglichen Randbedingungen  liegt damit ein nichtlineares Gleichungssystem in den Variablen  vor, das in den meisten Fällen mit Hilfe des Newton-Verfahrens gelöst wird; problematisch kann dabei die Startinitialisierung von  sein. In obigem Beispiel mit zwei Randwertbedingungen könnte z.B. die Verbindungsgerade von  nach  zur Initialisierung von  verwendet werden. Das Mehrzielverfahren lässt sich gut mit der Methode der kleinsten Quadrate kombinieren, wenn die zu schätzenden Parameter in einem Differentialgleichungsmodell auftreten.

3a) Numerische Methoden zur Integration partieller Differentialgleichungssysteme hängen sehr vom Typ des Systems ab. Insbesondere unterscheiden sich diese Methoden hinsichtlich der Diskretisierung, die das Differentialgleichungssystem in ein endliches System algebraischer Gleichungen überführt. Randwertprobleme führen auf elliptische Systeme; hier eignen sich die Finite-Elemente-Methode (FEM; die Lösung wird durch endliche Linearkombinationen bekannter Basisfunktionen gewonnen) oder das Finite-Differenzen-Verfahren (FDV; der Integrationsbereich wird durch ein endliches Gitter ersetzt und Ableitungen werden durch Differenzen ersetzt). Zeitabhängige Probleme, die stets neben möglichen (geometrischen Randbedingungen) Anfangswertbedingungen enthalten und zeitlich instationäre Probleme beschreiben, führen auf parabolische oder hyperbolische Systeme; hier sind die erwähnten Verfahren nur bedingt verwendbar; insbesondere sind explizite FDV (der gegenwärtige Zeitschritt hängt nur von früheren ab) nur bedingt stabil, während implizite FDV (das Differenzenschema kann nicht explizit hinsichtlich des gegenwärtigen Zeitsschritts aufgelöst werden) unbedingt stabil sind. Parabolische partielle Differentialgleichungssysteme lassen sich mit Hilfe der Methode der Linien (MdL) auf ein System gewöhnlicher Differentialgleichungen zurückführen. Dies entspricht einer Finite-Differenzen- oder Finite-Elemente-Diskretisierung im räumlichen Bereich. Die MdL wird besonders häufig verwendet bei zeitabhängigen partiellen Differentialgleichungsmodellen mit nur einer räumlichen Variablen und führt auf ein gekoppeltes System von  gewöhnlichen Differentialgleichungen, wenn  die Anzahl der Diskretisierungspunkte bezeichnet. Beispiel: Die Diffusionsgleichung

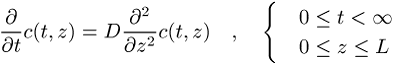
mit Diffusionskoeffizienten  erlaubt die räumliche Diskretisierung nach

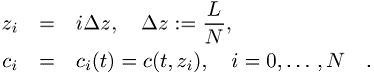
Approximiert man die räumliche Ableitung  durch ihre finiten Differenzen

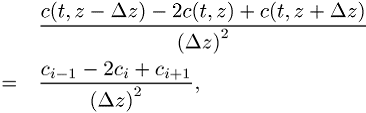
so kann die Diffusionsgleichung durch die  gewöhnlichen Differentialgleichungen

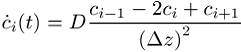
ersetzt werden. Hyperbolische Differentialgleichungen leiten sich meist aus strömungsmechanischen Problemen ab (Euler-Gleichungen, Navier-Stokes-Gleichungen), die aus first-principles abgeleitete Erhaltungssätze für Masse, Impuls und Energie darstellen; sie treten häufig in der Gasdynamik, im Flugzeugbau oder bei re-entry Problemen von Raumfahrzeugen auf, führen auf Unterschall- und Überschallproblematik, die sich in Form von Unstetigkeiten (Schocks, Kontaktdiskontinuitäten) in den Lösungen bemerkbar macht. Hier eignen sich besonders Finite-Volumen-Verfahren, die bei ihrer Diskretisierung darauf achten, dass die Erhaltungssätze strikt erfüllt sind (Beispiel: Godunow-Verfahren mit exaktem Riemann-Löser) und somit in der Lage sind, die Unstetigkeiten mit guter Genauigkeit wiederzugeben. Insbesondere bei der numerischen Integration mehrdimensionaler partieller Differentialgleichungssysteme kommen adaptive Verfahren und Multigrid-Methoden zum Einsatz; bei beiden Verfahren wird die Diskretisierung und insbesondere die räumliche Gittergrösse dem lokalen Verhalten des Systems angepasst.

numerische Integration: Intervalle, Gewichte und Polynome beim Gaussschen Integrationsverfahren.

bottom-alt:solid black .6pt;padding:0cm 3.55pt 0cm 3.55pt\'>	bottom:solid black 1.0pt;border-right:none; mso-border-top-alt:solid black .6pt;mso-border-bottom-alt:solid black .6pt; padding:0cm 3.55pt 0cm 3.55pt\'>	bottom-alt: solid black .6pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'> Polynom
	1
bottom:solid black 1.0pt;border-right:none; mso-border-left-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'>	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 3.55pt 0cm 3.55pt\'>