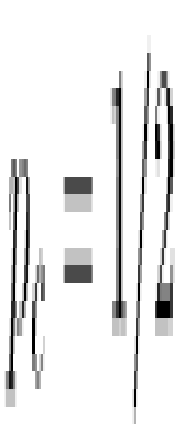Perkolationstheorie

Petra Nordinghaus-Martin
Thermodynamik und statistische Physik
bottom:.0001pt\'>Die Perkolationstheorie beschäftigt sich allgemein mit der Entstehung und Beschreibung komplexer, meist ungeordneter Strukturen, die sich aus einfachen Bestandteilen zusammensetzen. Erste Modelle wurden bereits Anfang der 40er Jahre von P.J. Flory und W.H. Stockmeyer zur qualitativen Beschreibung der Polymergelierung (Gele) entwickelt. Der Name »Perkolationstheorie« leitet vom lateinischen »percolare« mit der Bedeutung »durchdringen, durchseihen« oder auch »eindringen« ab. Er wurde 1957 in einer Publikation von S.R. Brodbent und J.M. Hammersley geprägt und deutet auf eine wichtige Fragestellung der Perkolationstheorie hin: Unter welchen Bedingungen entstehen makroskopisch zusammenhängende komplexe Strukturen, die eine Verbindung zwischen meist räumlich entfernten Punkten oder Gebieten schaffen? Wann ist beispielsweise das Röhrensystem in einem porösen Medium so beschaffen, dass eine Flüssigkeit dieses Medium durchdringen kann?
bottom:.0001pt\'>Gegen Ende der 70er Jahre hat sich die Perkolationstheorie von einem Teilgebiet der statistischen Mechanik zu einem eigenständigen Forschungsgebiet etabliert. Dies hängt nicht zuletzt mit der Entwicklung schnellerer und grösserer Computer zusammen, mit deren Hilfe auch komplexe Modelle der Perkolationstheorie numerisch intensiver untersucht werden können.
bottom:.0001pt\'>Die wesentlichen Methoden der Perkolationstheorie sind die Entwicklung mathematischer Modelle, die Anwendung und Erweiterung von Verfahren der statistischen Mechanik und natürlich numerische Verfahren wie die Simulation von Systemen auf einem Computer. Neben der Festkörperphysik steht die Perkolationstheorie in engem Kontakt mit der Hydrodynamik, der Physik der Polymere und der Chemie, ihre Anwendungsmöglichkeiten gehen jedoch weit über die Naturwissenschaften hinaus.
bottom:.0001pt\'>
bottom:.0001pt\'>1. Cluster
bottom:.0001pt\'>Ein zentraler Begriff in der Perkolationstheorie ist der Begriff des Clusters. Er kann als Modell eines porösen Mediums dienen, aber auch für andere ungeordnete Strukturen stehen, z.B. für stark verzweigte Makromoleküle, die Verteilung bestimmter Bestandteile in Legierungen, für ein ungeordnetes Netzwerk elektrischer Leiter, oder auch abstrakt für ein komplexes System von Relationen.
bottom:.0001pt\'>Ein Cluster ist mathematisch ein Graph, d.h. eine Menge von Punkten (in der Perkolationstheorie oft Sites genannt) sowie Verbindungslinien zwischen einzelnen Punkten (Bonds), der in eine Ebene oder den dreidimensionalen Raum eingebettet ist, oder als Teil eines regulären Gitters aufgefasst wird. Verallgemeinerungen zu d-dimensionalen Räumen bzw. Gittern werden ebenfalls untersucht. Für manche Anwendungen werden den Sites oder Bonds des Clusters noch bestimmte Eigenschaften zugeschrieben, z.B. eine mittlere Dicke, der Wert eines elektrischen Widerstands, ein chemischer Reaktions- bzw. Absorptionskoeffizient usw.
bottom:.0001pt\'>Clustereigenschaften dienen zur Charakterisierung und Beschreibung von Clustern. Für einen zusammenhängenden Cluster kann man generell intrinsische und extrinsische Clustereigenschaften unterscheiden. Intrinsische Clustereigenschaften lassen sich einzig aus der Struktur des Graphen, d.h. den kombinatorischen Relationen der Nachbarschaftsverhältnisse von Sites, definieren. Extrinsische Clustereigenschaften hingegen beziehen sich auf die Einbettung des Graphen in einer Fläche, einem Raum, oder auf einem regulären Gitter.
bottom:.0001pt\'>Zu den intrinsischen Clustereigenschaften zählt beispielsweise die sog. Masse s des Clusters, d.h. die Anzahl der Sites (manchmal auch die Anzahl der Bonds), aus denen der Cluster besteht. Eine wichtige extrinsische Eigenschaft zur Charakterisierung eines Clusters ist sein Umfang (Clusteroberfläche), d.h. die Anzahl der Punkte des einbettenden Gitters, die zu einem Site des Clusters benachbart sind, aber nicht selber zum Cluster gehören.
bottom:.0001pt\'>Zwei Sites eines
zusammenhängenden Clusters kann man sowohl intrinsisch als auch extrinsisch
einen Abstand zuordnen. Intrinsisch definiert man den Abstand der Sites als die
Länge (=Anzahl der Bonds) eines kürzesten Verbindungsweges auf dem Cluster
zwischen den Sites. Extrinsisch wählt man meist den euklidischen Abstand, der
durch die Einbettung in einen Raum oder ein Gitter definiert ist. Clustereigenschaften,
die von einem Abstandsbegriff abhängen, können sich sehr unterscheiden, je
nachdem, welche der beiden Definitionen benutzt wird. So gibt es einen
intrinsischen bzw. extrinsischen Durchmesser eines Clusters (der maximale
Abstand zwischen zwei Sites des Clusters) oder auch einen intrinsischen bzw.
extrinsischen Gyrationsradius. Beide Grössen definieren eine lineare Ausdehnung
eines Clusters. Das gleiche gilt für die Korrelationslänge ![]() , die den exponentiellen Abfall der
Clusterkorrelationsfunktion beschreibt.
, die den exponentiellen Abfall der
Clusterkorrelationsfunktion beschreibt.
bottom:.0001pt\'>Man bezeichnet einen
Cluster als perkolierend, wenn er gegenüberliegende Ränder des einbettenden
Raumes bzw. Gitters verbindet. Denkt man sich den Cluster als elektrisch
leitendes System, bei dem die Bonds Widerstände repräsentieren, und wird
zwischen den Rändern eine Spannung angelegt, so kann durch einen perkolierenden
Cluster ein Strom fliessen. Die Leitfähigkeit ![]() eines perkolierenden Clusters hängt nur von
seinem Rückgrat ab, d.h. dem Teil des Clusters, durch den tatsächlich ein Strom
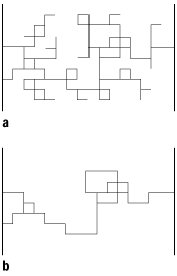
fliesst (siehe [1]Abb. 1). Das Komplement des Rückgrats
bezeichnet man auch als lose Enden (dangling ends). Innerhalb des Rückgrats
kommt den einfach-zusammenhängenden Bonds eine besondere Bedeutung zu: Entfernt
man einen einfach-zusammenhängenden Bond aus dem Rückgrat des Clusters, so
zerfällt er in zwei Hälften, d.h. er ist kein perkolierender Cluster mehr. Für
die Zerlegung eines Clusters in einfach-zusammenhängende Bonds des Rückgrats,
mehrfach-zusammenhängende Bonds des Rückgrats und lose Enden hat H.E.Stanley
den Begriff der »Rot-Blau-Gelb-Zerlegung« geprägt.
eines perkolierenden Clusters hängt nur von
seinem Rückgrat ab, d.h. dem Teil des Clusters, durch den tatsächlich ein Strom
fliesst (siehe [1]Abb. 1). Das Komplement des Rückgrats
bezeichnet man auch als lose Enden (dangling ends). Innerhalb des Rückgrats
kommt den einfach-zusammenhängenden Bonds eine besondere Bedeutung zu: Entfernt
man einen einfach-zusammenhängenden Bond aus dem Rückgrat des Clusters, so
zerfällt er in zwei Hälften, d.h. er ist kein perkolierender Cluster mehr. Für
die Zerlegung eines Clusters in einfach-zusammenhängende Bonds des Rückgrats,
mehrfach-zusammenhängende Bonds des Rückgrats und lose Enden hat H.E.Stanley
den Begriff der »Rot-Blau-Gelb-Zerlegung« geprägt.
bottom:.0001pt\'>Viele
Clustereigenschaften lassen sich erst im Grenzfall unendlich grosser Cluster
definieren. Dazu zählen insbesondere verschiedene Dimensionsbegriffe, die sich
einem Cluster zuordnen lassen. Die Clusterdimension D
ist durch eine Skalenrelation der Form ![]() definiert, wobei s
die Anzahl aller Sites ist, die sich innerhalb eines Abstands l von einem Referenzpunkt (über den gemittelt wird)
befinden. Für grosse Werte von l erwartet man ein
Skalengesetz obiger Form, wobei die Dimension D
nicht unbedingt ganzzahlig sein muss. Je nach verwendetem Abstandsfunktional l ist D die intrinsische oder
extrinsische Clusterdimension. Ist D nicht
ganzzahlig, so handelt es sich bei dem Cluster um ein Fraktal.
definiert, wobei s
die Anzahl aller Sites ist, die sich innerhalb eines Abstands l von einem Referenzpunkt (über den gemittelt wird)
befinden. Für grosse Werte von l erwartet man ein
Skalengesetz obiger Form, wobei die Dimension D
nicht unbedingt ganzzahlig sein muss. Je nach verwendetem Abstandsfunktional l ist D die intrinsische oder
extrinsische Clusterdimension. Ist D nicht
ganzzahlig, so handelt es sich bei dem Cluster um ein Fraktal.
bottom:.0001pt\'>Ein weiterer nützlicher Dimensionsbegriff ist die spektrale Dimension eines Clusters, die über die Rückkehrwahrscheinlichkeit eines Diffusionsprozesses bzw. Random Walks (s.u.) auf dem Cluster definiert wird. Auch der anomale Diffusionsexponent (anomale Diffusion) ist eine wichtige Clustereigenschaft. Clusterdimension, spektrale Dimension und anomaler Diffusionskoeffizient lassen sich natürlich auch für wichtige Teilgraphen eines Clusters, beispielsweise das Rückgrat, bestimmen.
bottom:.0001pt\'>Für einen unendlichen Cluster ist seine Grösse bzw. Masse nicht mehr definiert. In diesem Fall hat sich die Clusterstärke P als sinnvolle Charakterisierung erwiesen. P ist definiert als die Wahrscheinlichkeit, dass ein beliebiger Gitterpunkt Teil des unendlichen Clusters ist. Die Clusterstärke ist somit eine extrinsische Clustereigenschaft.
bottom:.0001pt\'>Bisher haben wir nur
Clustereigenschaften eines einzelnen zusammenhängenden Clusters erwähnt.
Oftmals interessiert man sich in der Perkolationstheorie aber für ein Ensemble
von Clustern. So liefern die Perkolationsmodelle (s.u.) meist eine
Clusterkonfiguration, d.h. ein Ensemble von unzusammenhängenden Clustern. Für
ein solches Ensemble lassen sich Verteilungsfunktionen der Clustereigenschaften
angeben, die sog. Clusterzahlen. Eine wichtige Clusterzahl ist ![]() , die Anzahl der Cluster der Masse s pro Gitterpunkt. Daraus erhält man die
Wahrscheinlichkeit
, die Anzahl der Cluster der Masse s pro Gitterpunkt. Daraus erhält man die
Wahrscheinlichkeit ![]() ,
dass ein beliebig herausgegriffener Gitterpunkt Teil eines Clusters der Masse s ist. Die mittlere Clustergrösse ist dann durch den
Erwartungswert von s
,
dass ein beliebig herausgegriffener Gitterpunkt Teil eines Clusters der Masse s ist. Die mittlere Clustergrösse ist dann durch den
Erwartungswert von s
bottom:.0001pt\'>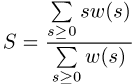
bottom:.0001pt\'>gegeben. Weiterhin ist
bottom:.0001pt\'>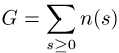
bottom:.0001pt\'>gleich der mittleren Anzahl von Clustern pro Site, unabhängig von ihrer Grösse.
bottom:.0001pt\'>
bottom:.0001pt\'>2. Perkolationsmodelle
bottom:.0001pt\'>Im Idealfall dienen komplexe physikalische Systeme als Vorlage, und die Perkolationstheorie sucht nach einfachen Modellen, Cluster mit den Eigenschaften dieser Systeme zu generieren. Oftmals ist der eingeschlagene Weg jedoch umgekehrt: Die Perkolationstheorie entwickelt bestimmte Verfahren zur Generierung von Clustern und untersucht - analytisch oder numerisch - welche Eigenschaften die so erzeugten Cluster haben.
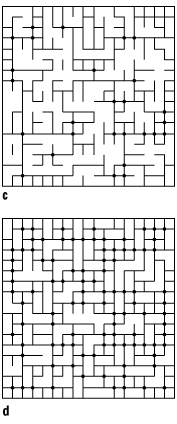
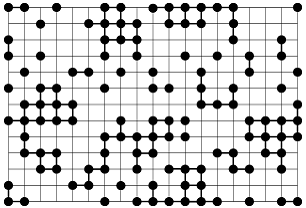
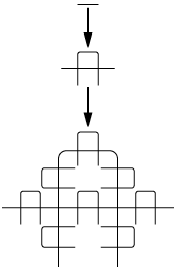
bottom:.0001pt\'>Die einfachsten Perkolationsmodelle zur Erzeugung von Clusterkonfigurationen sind die Site-Perkolation und die Bond-Perkolation. Bei der Bond-Perkolation werden die Linien eines regulären Gitters mit einer unkorrelierten Wahrscheinlichkeit p markiert bzw. besetzt und dadurch als Teil eines Clusters definiert (vgl. [2]Abb. 2). Bei der Site-Perkolation werden zunächst die Gitterpunkte mit einer Wahrscheinlichkeit p besetzt. Anschliessend wird durch eine zweite Vorschrift entschieden, welche der besetzten Gitterpunkte durch Linien verbunden werden. Für die "nächste-Nachbar"-Site-Perkolation werden alle Gitterlinien besetzt, für die beide Endpunkte besetzt sind ([3]Abb. 3). Eine einfache Verallgemeinerungen dieser Verfahren ist die Site-Bond-Perkolation.
bottom:.0001pt\'>Kompliziertere Modelle berücksichtigen Korrelationen zwischen besetzten Sites oder Bonds. So kann man beispielsweise eine typische Konfiguration des Ising-Modells bei gegebener Temperatur vorgeben, und alle Gitterlinien, an deren Endpunkten die Werte der Spinvariablen positiv sind, als Teil eines Clusters auffassen. Für Ising-Konfigurationen bei unendlicher Temperatur gelangt man zur unkorrelierten Site-Perkolation zurück, wobei das Magnetfeld im Ising-Modell die Besetzungswahrscheinlichkeit steuert.
bottom:.0001pt\'>Die angegebenen Methoden der Site-Perkolation und Bond-Perkolation sind rein statistischer Natur und sagen oft wenig über die Kinematik der Entstehung von Clustern aus. Es gibt jedoch auch Modelle, die das Wachstum eines Clusters beschreiben. Das folgende iterative Verfahren, das eine diskrete Zeitentwicklung simuliert, ist beispielsweise äquivalent zur Site-Perkolation: Ausgehend von einem Ursprungspunkt werden dessen Nachbarpunkte mit einer Wahrscheinlichkeit p besetzt und die besetzten Sites mit dem Ausgangspunkt verbunden. In einem zweiten Schritt werden alle noch nicht behandelten Nachbarsites von bereits besetzten Sites mit einer Wahrscheinlichkeit p besetzt und wiederum benachbarte markierten Sites verbunden. Dieses Verfahren lässt sich iterativ fortsetzen, bis bei einem Schritt keine neuen Sites hinzugekommen sind. Man simuliert so die schrittweise Entstehung eines einzelnen Clusters aus der Site-Perkolation. Für eine gute Statistik muss dieser Prozess genügend oft wiederholt werden.
bottom:.0001pt\'>
bottom:.0001pt\'>3. Die Perkolationsschwelle
bottom:.0001pt\'>Von besonderem
Interesse für die Perkolationstheorie sind die gemittelten Eigenschaften
typischer Cluster als Funktion der Modellparameter, beispielsweise der
Besetzungswahrscheinlichkeiten p. In allen oben
genannten Fällen gibt es eine sog. Perkolationsschwelle ![]() , oberhalb derer im thermodynamischen
Grenzfall mit Wahrscheinlichkeit 1 ein Cluster unendlicher Grösse existiert,
wohingegen unterhalb der Schwelle die Wahrscheinlichkeit für einen unendlichen
Cluster gleich Null ist. Bei endlichen Gittern betrachtet man meist die
Wahrscheinlichkeit für das Auftreten eines perkolierenden Clusters. Diese
Wahrscheinlichkeit nähert sich im thermodynamischen Grenzfall der scharfen
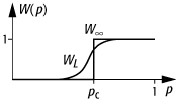
Stufenfunktion (siehe [4]Abb. 4).
, oberhalb derer im thermodynamischen
Grenzfall mit Wahrscheinlichkeit 1 ein Cluster unendlicher Grösse existiert,
wohingegen unterhalb der Schwelle die Wahrscheinlichkeit für einen unendlichen
Cluster gleich Null ist. Bei endlichen Gittern betrachtet man meist die
Wahrscheinlichkeit für das Auftreten eines perkolierenden Clusters. Diese
Wahrscheinlichkeit nähert sich im thermodynamischen Grenzfall der scharfen
Stufenfunktion (siehe [4]Abb. 4).
bottom:.0001pt\'>Im Sinne der
statistischen Mechanik handelt es sich bei diesem Phänomen um einen
Phasenübergang, bei dem sich qualitative Eigenschaften des Systems verändern.
Viele Clustereigenschaften verschwinden bzw. divergieren an der
Perkolationsschwelle, so dass man wie in der statistischen Mechanik kritische Exponenten
(Phasenübergänge und kritische Phänomene) definieren kann. Nähert man sich der
Perkolationsschwelle von unten, so divergieren z.B. die mittlere Clusterzahl ![]() , die mittlere Clustergrösse
, die mittlere Clustergrösse ![]() und die
Clusterkorrelationslänge
und die
Clusterkorrelationslänge ![]() und
definieren die kritischen Exponenten
und
definieren die kritischen Exponenten ![]() ,
, ![]() und
und ![]() :
:
bottom:.0001pt\'>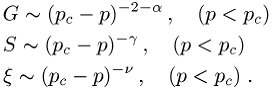
bottom:.0001pt\'>Nähert man sich der
Perkolationsschwelle von oben, so verschwinden die Clusterstärke ![]() und die Leitfähigkeit
und die Leitfähigkeit ![]() und definieren die kritischen
Exponenten
und definieren die kritischen
Exponenten ![]() und
und ![]() :
:
bottom:.0001pt\'>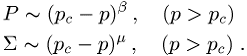
bottom:.0001pt\'>Die kritischen Exponenten sind oft von den Details der Modelle wie dem Gittertyp unabhängig, was wie in der statistischen Mechanik auf die Existenz von Universalitätsklassen zurückgeführt wird.
bottom:.0001pt\'>Während viele Clustereigenschaften, insbesondere die Clusterdimension, oberhalb bzw. unterhalb der Perkolationsschwelle eher auf reguläre Cluster hindeuten, handelt es sich bei den perkolierenden Clustern genau an der Perkolationsschwelle um Fraktale. Daher sind die ersten auftretenden perkolierenden Cluster, wenn man sich von unten der Perkolationsschwelle nähert, auch von besonderem Interesse.
bottom:.0001pt\'>
bottom:.0001pt\'>4. Dynamische Prozesse auf Clustern
bottom:.0001pt\'>Bereits 1976 hat Pierre-Gilles de Gennes Diffusionsprozesse bzw. Random Walks auf Clustern untersucht und dafür den Begriff der Ameise im Labyrinth geprägt. Von besonderem Interesse sind in diesem Zusammenhang natürlich die fraktalen perkolierenden Cluster unmittelbar an der Perkolationsschwelle. Hier erwartet man anomale Diffusion und nicht-ganzzahlige spektrale Dimensionen.
bottom:.0001pt\'>Unterschiedliche Random-Walk-Vorschriften auf einem Cluster wurden gelegentlich durch die Angabe von Tiernamen bezeichnet. Eine »blinde Ameise« beispielsweise versucht in alle Richtungen zu gehen, die durch das Gitter möglich sind, muss aber stehen bleiben, wenn die gewählte Richtung keinem Bond des Clusters entspricht. Eine »kurzsichtige Ameise« wählt immer Schritte auf dem Cluster, allerdings nur zu benachbarten Sites. Ein »Schmetterling« kann in einem Schritt auch grössere Distanzen überwinden und »Parasiten« diffundieren auf Gittertieren (s.u.). Für die kritischen Exponenten sind die Details der Random-Walk-Vorschrift oft nicht relevant.
bottom:.0001pt\'>Ein interessanter dynamischer Prozess auf perkolierenden Clustern ist die sog. Invasionsperkolation. Hierbei repräsentiert der Cluster das Röhrensystem eines porösen Mediums. Von einer Seite des Clusters diffundiert eine Flüssigkeit in den Cluster und verdrängt eine andere Flüssigkeit zum gegenüberliegenden Rand hin. Da durch die eindringende Flüssigkeit oftmals Poren besetzt werden, so dass die andere Flüssigkeit nicht mehr abfliessen kann, bleiben grosse Bereiche im Cluster mit der ursprünglichen Flüssigkeit besetzt. Die Invasionsperkolation lässt sich ebenfalls durch Random-Walk-Prozesse auf einem Cluster simulieren.
bottom:.0001pt\'>
bottom:.0001pt\'>5. Methoden
bottom:.0001pt\'>In den vergangenen zwanzig Jahren wurde der Computer zum wichtigsten technischen Hilfsmittel der Perkolationstheorie. Nicht nur die verschiedenen Perkolationsmodelle zur Erzeugung von Clustern oder dynamische Prozesse auf Clustern lassen sich auf dem Computer simulieren, sondern auch die Analyse der Daten beispielsweise zur Bestimmung der Clustereigenschaften wäre ohne die Hilfe von Computern kaum noch möglich. Ein Zweig der Perkolationstheorie beschäftigt sich nahezu ausschliesslich mit der Entwicklung von Computer-Algorithmen zur Analyse von Clustern in einem Clusterensemble.
bottom:.0001pt\'>Für viele Perkolationsmodelle lassen sich Näherungen in Form von Reihenentwicklungen angeben. So kann man bei der Site- und Bond-Perkolation eine Entwicklung nach kleinen Werten der Besetzungswahrscheinlichkeiten p vornehmen. Es tragen in diesem Fall nur kleine Cluster bei - sog. Gittertiere - , deren Formen und Kombinatorik noch analytisch angegeben werden können. Mit Hilfe von Padé-Methoden (Padé-Approximation) findet man meist gute Abschätzungen der Konvergenzradien dieser Reihen und damit auch der kritischen Punkte bzw. der Perkolationsschwellen.
bottom:.0001pt\'>In seltenen Fällen sind exakte Lösungen der Modelle in der Perkolationstheorie bekannt. Eine Ausnahme bilden Modelle auf eindimensionalen Gittern oder auf dem (unendlichdimensionalen) Bethe-Gitter. Für diese beiden Grenzfälle lassen sich viele Modelle geschlossen lösen, und man erhält so Hinweise auf das qualitative Verhalten mancher Clustereigenschaften als Funktion der Dimension.
bottom:.0001pt\'>Für einige
zweidimensionale Modelle sind die exakten Werte der Perkolationsschwelle
bekannt, beispielsweise für die Bond-Perkolation auf dem Dreiecksgitter (![]() ), auf dem Quadratgitter (
), auf dem Quadratgitter (![]() ) und auf dem Sechsecksgitter
(
) und auf dem Sechsecksgitter
(![]() ), oder die
Site-Perkolation auf dem Dreiecksgitter (
), oder die
Site-Perkolation auf dem Dreiecksgitter (![]() ).
).
bottom:.0001pt\'>Als sehr fruchtbar zur Beschreibung der Phänomene in der Nähe der Perkolationsschwelle haben sich Methoden der Renormierungsgruppentheorie (Renormierung) sowie Skalenansätze erwiesen.
bottom:.0001pt\'>Ein Skalenansatz für
die Clusterzahl ![]() der
Form
der
Form
bottom:.0001pt\'>![]()
bottom:.0001pt\'>mit einer geeigneten
Funktion ![]() erlaubt es,
die kritischen Exponenten der Momente von
erlaubt es,
die kritischen Exponenten der Momente von ![]() (dazu zählen z.B. die mittlere Clusterzahl, die
Clusterstärke und die mittlere Clustergrösse) durch die Exponenten
(dazu zählen z.B. die mittlere Clusterzahl, die
Clusterstärke und die mittlere Clustergrösse) durch die Exponenten ![]() und
und ![]() auszudrücken. Dadurch ergeben sich Relationen
zwischen den kritischen Exponenten, die als Test der Skalenhypothese
herangezogen werden können.
auszudrücken. Dadurch ergeben sich Relationen
zwischen den kritischen Exponenten, die als Test der Skalenhypothese
herangezogen werden können.
bottom:.0001pt\'>Aus obigem Skalenansatz lässt sich beispielsweise das Rushbrookesche Skalengesetz leicht herleiten:
bottom:.0001pt\'>![]()
bottom:.0001pt\'>Auch Verfahren des Finite-Size-Scalings (d.h. Skalenansätze, bei denen die Gittergrösse einer der Parameter ist, bezüglich derer die physikalischen Grössen wie z.B. die Clusterzahlen oder die Leitfähigkeit einem Skalengesetz genügen) werden mit Erfolg angewandt (Skalenverhalten).
bottom:.0001pt\'>Renormierungsgruppentransformationen können sowohl im Impuls- als auch im Ortsraum durchgeführt werden. Für die Beschreibung der Systeme in der Nähe der Perkolationsschwelle liefern oft einfache Ortsraumrenormierungsgruppentransformationen für kleine Gitterzellen überraschend gute Resultate. In diesen Fällen lassen sich die Renormierungsgruppengleichungen meist noch analytisch aufstellen. Renormierungsgruppentransformationen grösserer Zellen können im allgemeinen nur numerisch behandelt werden.
bottom:.0001pt\'>Zur Untersuchung der fraktalen Eigenschaften von Clustern an der Perkolationsschwelle werden oft »regelmässige« Fraktale mit bekannten Eigenschaften wie der Sierpinski-Teppich oder die Mandelbrot-Given-Kurve (siehe [5]Abb. 5) und entsprechende Verallgemeinerungen herangezogen. Wegen der Selbstähnlichkeit dieser Fraktale lassen sich hier Renormierungsgruppentransformationen exakt formulieren und somit die relevanten kritischen Exponenten bzw. Dimensionen berechnen.
6. Anwendungen
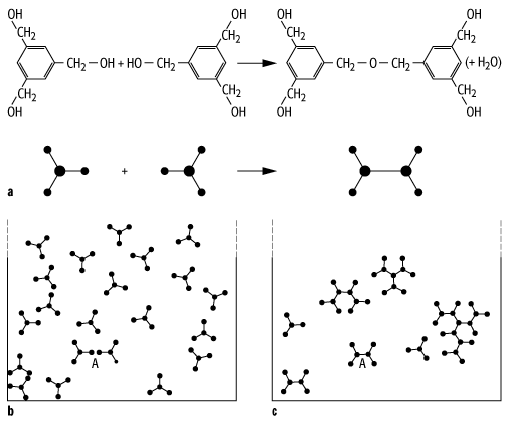
Das Modell der Bond-Perkolation wurde Anfang der 40er Jahre von P.J. Flory und W.H. Stockmeyer formuliert und untersucht. Man erhofft sich von diesem Modell ein besseres Verständnis der Mechanismen bei der Gelierung (Gele). In Abhängigkeit gewisser äusserer Parameter wie Temperatur, Dichte oder Druck verbinden sich in diesem Fall Moleküle mit mehreren chemisch aktiven Enden zu makroskopischen Clustern, die zu einer Verfestigung der ursprünglichen Lösung führen (siehe [6]Abb.6). Das Hartwerden eines Eies beim Kochen ist ein Alltagsbeispiel eines solchen Prozesses. Ob diese Mechanismen durch das einfache Modell der Bond-Perkolation jedoch genau beschrieben werden, ist nach wie vor umstritten.
Viele Anwendungen der Perkolationstheorie entstammen natürlich dem Bereich der Physik, insbesondere der Festkörperphysik. Die Site-Perkolation ist beispielsweise ein Modell für die Entstehung spontaner globaler Magnetisierung in Legierungen. Stellen wir uns eine Legierung aus zwei Bestandteilen A und B vor. Die A-Atome haben ein magnetisches Moment, die B-Atome nicht. Sind zwei A-Atome benachbart, so kommt es bei tiefen Temperaturen zu einer parallelen Ausrichtung der Momente. Es erhebt sich nun die Frage, bei welcher Konzentration der A-Atome in der Legierung es zur Ausbildung von makroskopischen Clustern mit spontaner Magnetisierung kommt. Ist die Wechselwirkung zwischen A-A-Atompaaren dieselbe wie zwischen A-B-Atompaaren, so haben wir hier ein Beispiel für eine unkorrelierte Site-Perkolation. Andernfalls gibt es noch Korrelationen zwischen der Anordnung der A-Atome und B-Atome, und wir finden die oben erwähnte Erweiterung der Site-Perkolation zur Clusterentstehung in einem Ising-Modell. Mit solchen und ähnlichen Modellen hat die Perkolationstheorie ganz allgemein zu einem besseren Verständnis von Phasenübergängen und der Bildung geordneter Strukturen beigetragen.
Die Perkolationstheorie findet auch Anwendung bei der Konstruktion schnellerer Computeralgorithmen zur Simulation von Gittermodellen (Monte-Carlo-Simulation). 1987 haben R.H. Swendsen und J.S. Wang erstmals sog. Clusteralgorithmen entwickelt, bei denen die Veränderungen an einer Konfiguration für einen Update nicht lokal an einzelnen Punkten oder Linien vorgenommen werden, sondern innerhalb globaler Bereiche, den Clustern. Solche Verfahren zeichnen sich durch sehr kurze »zeitliche« Korrelationen zwischen den Konfigurationen aus und sind daher besonders in der Nähe von kritischen Punkten sehr effizient. Andererseits benötigen sie aber auch einen grossen Rechenaufwand zur Berechnung der Cluster.
Die Dynamik der Clusterentstehung bzw. Clusterausbreitung kann als Modell für die Ausbreitung von Waldbränden oder Epidemien dienen. Das Überspringen des Feuers von einem Baum auf einen nächsten Baum oder die Übertragung einer Krankheit von einem Organismus auf einen nächsten Organismus entspricht den Bonds eines Clusters. Je nach den Werten der Parameter (beispielsweise der Dichte der Bäume bzw. Organismen) kommt es zur Ausbildung eines grossen Clusters, d.h. zu einem flächendeckenden Waldbrand bzw. einer ausgedehnten Epidemie. In der Astrophysik werden Modelle der Perkolationstheorie zur Erklärung der Propagation der Sternentstehung in Galaxien verwandt, andere Perkolationsmodelle dienen der Beschreibung der Ausbreitung von Bruchstellen in der Bruchmechanik.
Typische Problemstellungen der Perkolationstheorie ergeben sich auch bei der Auswertung von Probebohrungen bei der Ölgewinnung. Hier geht es z.B. um die Frage, inwieweit sich aus einer Materialprobe die Ausdehnung und Beschaffenheit eines Ölfeldes bestimmten lässt. Deutet die Beschaffenheit einer Probe eher auf ein grosses, zusammenhängendes Ölfeld, oder eher auf kleine, unzusammenhängende Cluster hin? Wie gross ist die Wahrscheinlichkeit, dass eine zweite Bohrung in einem bestimmten Abstand von der ersten Bohrung auf dasselbe Ölfeld trifft? Wie müssen die Bohrungen angeordnet werden, so dass ein möglichst grosser Anteil des Öls tatsächlich abgepumpt werden kann? Solche und ähnliche Fragen lassen sich mit Hilfe der Perkolationstheorie angehen.
Dynamische Aspekte der Perkolationstheorie treten beim Problem der Kontamination von Erde nach einem Unfall mit giftigen Chemikalien auf. Hier geht es um die Frage, wieweit und wie schnell sich die Chemikalie auf Grund von Diffusionsprozessen in einem porösen Material wie dem Erdreich ausbreiten kann.
Die Perkolationstheorie findet heute in vielen Bereichen auch ausserhalb der Naturwissenschaften Anwendung, beispielsweise bei der Beschreibung der Expansion und Verknüpfung bestimmter Industriezweige in den Wirtschaftswissenschaften oder bei der Optimierung des Fliessverhaltens des Verkehrs in einer Grossstadt. Die hier angegebene Liste von Anwendungsbeispielen kann daher nur einen kleinen Einblick in die Möglichkeiten der Perkolationstheorie geben und ist bei weitem nicht vollständig.
Literatur:
Weiterführende Literatur und Übersichtsartikel:
D. Stauffer und A. Aharony: Perkolationstheorie - Eine Einführung; VCH-Verlag, Weinheim, 1995.
M. Sahimi: Flow and Transport in Porous Media and Fractured Rock; VCH-Verlag, Weinheim, 1995.
J.W. Essam: Percolation Theory; Rep. Prog. Phys. Vol.43 (1980) 833-912.
H. Kesten: Percolation Theory for Mathematicians, Birkhäuser, Boston, 1982.
Perkolationstheorie 1: Perkolierender Cluster (a) und sein Rückgrat in der Bond-Perkolation.
Perkolationstheorie 2: Bond-Perkolation für vier verschiedene Besetzungswahrscheinlichkeiten: a) p = 0,2, b) p = 0,4, c) p = 0,6 und d) p = 0,8.
Perkolationstheorie 3: Site-Perkolation auf dem Quadratgitter bei einer Besetzungswahrscheinlichkeit p = 0,5. (aus: Sahimi, VCH 1995)
Perkolationstheorie
4: Wahrscheinlichkeit für das Vorhandensein eines unendlichen Clusters (![]() ) bzw. perkolierenden Clusters
auf einem endlichen Gitter der linearen Ausdehnung L
(WL) als Funktion der
Besetzungswahrscheinlichkeit.
) bzw. perkolierenden Clusters
auf einem endlichen Gitter der linearen Ausdehnung L
(WL) als Funktion der
Besetzungswahrscheinlichkeit.
Perkolationstheorie 5: Die ersten Schritte zur Konstruktion der Mandelbrot-Given-Kurve. Bei jeder Iteration wird das Einheitssegment durch 8 Segmente ersetzt.
bottom:.0001pt;border:none; padding:0cm\'>Perkolationstheorie 6: Polymergelierung von Trimethylbenzol. Im unteren Teil sind zwei verschiedene Stadien der Clusterbildung skizziert.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.