Algebraische Quantenfeldtheorie

Irene Kramer-Schwenk
bottom:.0001pt\'>Die Algebraische Quantenfeldtheorie (AQFT) ist eine Beschreibung der Physik von relativistischen Quantensystemen, insbesondere von Elementarteilchen. Sie wurde in den sechziger Jahren von R. Haag, D. Kastler, H.-J. Borchers und H. Araki begründet. Wie die axiomatische Quantenfeldtheorie untersucht die AQFT den allgemeinen Rahmen von quantenfeldtheoretischen Modellen, um konzeptionelle Schwierigkeiten mit störungstheoretischen und euklidischen Zugängen aufzulösen. Sie basiert auf der (als gegeben angenommenen und mit weiteren Strukturen ausgestatteten, s.u.) Algebra der lokalen Observablen anstelle der eigentlichen Quantenfelder, von denen diese möglicherweise erzeugt wird.
bottom:.0001pt\'>Die AQFT analysiert das komplexe Zusammenspiel von fundamentalen physikalischen Prinzipien, insbesondere der Lokalität in Raum und Zeit und der Spektrumsbedingung in Energie und Impuls. Sie entwickelt analytische Strategien, um aus der Algebra und ihren Darstellungen strukturelle Aussagen über die betrachteten Systeme herzuleiten und beispielsweise den Teilcheninhalt der Theorie zu bestimmen; damit ist dieser nicht an die apriorischen Felder einer phänomenologischen Lagrangefunktion geknüpft, sondern ist vielmehr ein dynamischer Aspekt.
bottom:.0001pt\'>Das Ziel der AQFT ist es, den allgemeinen Rahmen einer relativistischen Quantentheorie abzustecken und zu verstehen, welche physikalischen Grundzüge sich modellübergreifend herausbilden müssen. Charakteristisch für ihre Methode ist die Übersetzung von phänomenologischen Eigenschaften der behandelten Systeme in klar definierte mathematische Begriffe; dadurch werden mathematische Lehrsätze anwendbar, um physikalische Zusammenhänge herzustellen. Die Algebra erweist sich als die geeignete universelle Sprache, um die universellen Prinzipien der Physik zu erfassen.
bottom:.0001pt\'>Daneben ermöglicht die AQFT auch die exakte Konstruktion von einfachen relativistischen Modellen (P(f)2- und Yukawa2-Modelle sowie konform-invariante Modelle in zwei Dimensionen). Ihre Methoden werden auch zum Studium von nichtrelativistischen Modellen der statistischen Mechanik (Spin-Systeme) angewandt.
bottom:.0001pt\'>Die Betonung der Algebra anstelle der Felder ist in der Tatsache begründet, dass (in der Sprache des Wightmanschen Zugangs zur Quantenfeldtheorie) grosse Klassen (Borchers-Klassen) von Feldern dieselben Streuprozesse beschreiben; so gehören etwa alle ungeraden Wick-Polynome eines freien massiven Feldes derselben Klasse an. Da alle Felder einer Borchers-Klasse auch dieselben lokalen Algebren erzeugen, und umgekehrt (z.B. in der Haag-Ruelle-Streutheorie) die Streuzustände allein aus den lokalen Algebren gewonnen werden können, müssen letztere als die relevanten Objekte betrachtet werden. Aus dieser Sicht bleiben Wightmansche Quantenfelder trotz ihrer Uneindeutigkeit ein nützliches Hilfsmittel, um die Lokalität und Poincaré-Kovarianz (s.u.) zu implementieren. Der Übergang zwischen der Wightmanschen und der algebraischen Formulierung ist noch nicht vollständig aufgeklärt; es ist jedoch bekannt, dass die AQFT auch Quantensysteme einschliesst, die nicht durch Felder beschreibbar sind.
bottom:.0001pt\'>Eine weitere
Motivation für die algebraische Sichtweise ergibt sich aus dem Umstand, dass
Quantensysteme mit unendlich vielen Freiheitsgraden (im Unterschied zur
Quantenmechanik) in der Regel sehr viele inäquivalente physikalische
Darstellungen besitzen. Diese beschreiben Klassen von Zuständen, zwischen denen
keine Interferenz möglich ist (Superauswahlregeln oder -Sektoren). Die
konzeptionelle Trennung zwischen der Algebra (dem physikalischen System) und
ihren Darstellungen (den möglichen Zuständen des Systems) ist in der AQFT von
vornherein verankert.
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Die Axiome der AQFT: Interpretation und Konsequenzen
bottom:.0001pt\'>Die AQFT formuliert ein System von Axiomen, in dem wir hier drei Klassen unterscheiden wollen:
bottom:.0001pt\'>- strukturelle Axiome, die der Quantennatur und dem Feldcharakter der zu beschreibenden Objekte Rechnung tragen (Hilbertraum, Lokalisierbarkeit, s.u.),
bottom:.0001pt\'>- relativistische Axiome, um den Anforderungen der Speziellen Relativitätstheorie zu genügen (Lokalität, Kausalität, Kovarianz, Spektrumsbedingung, s.u.) und
bottom:.0001pt\'>- eine Reihe von spezifischen Annahmen, die zur Kennzeichnung verschiedener Typen von Theorien oder Zuständen variiert werden können (Massenlücke, Haag-Dualität, Kompaktheit, innere Symmetrien, s.u.).
bottom:.0001pt\'>Diese Axiome sind hierbei nicht als feste Vorgaben zu verstehen, sondern sind selbst Gegenstand der Forschung und Diskussion in einem sich entwickelnden Gebiet; sie müssen stets physikalisch begründet und letztlich empirisch überprüft werden.
bottom:.0001pt\'>Observable und
Felder
bottom:.0001pt\'>In der Quantentheorie werden physikalische Messungen und Operationen durch "Observable" beschrieben. Diese sind als selbstadjungierte Operatoren auf einem Hilbertraum darstellbar, dessen Vektoren und Dichtematrizen reine und gemischte Zustände repräsentieren. Dadurch wird die Wahrscheinlichkeitsinterpretation sichergestellt, nach der Matrixelemente der Operatoren Übergangsamplituden oder Erwartungswerte sind. Die beschränkten Observablen bilden in jeder Darstellung eine konkrete C*-Algebra. Die Gesamtheit aller ihrer Darstellungen kann durch eine abstrakte C*-Algebra charakterisiert werden, für deren Studium die hochentwickelte mathematische Theorie der Operatoralgebren zur Verfügung steht.
bottom:.0001pt\'>Die moderne Physik geht davon aus, dass alle Elementarteilchen und ihre Wechselwirkungen durch orts- und zeitabhängige Quantenfelder beschrieben werden können, die den klassischen Feldbegriff von M. Faraday (Ortsabhängigkeit) mit einem dynamischen Gesetz (Zeitabhängigkeit) relativistisch - im Sinne der Speziellen Relativitätstheorie von A. Einstein - vereinigen und in die Quantentheorie übertragen. Zwar entsprechen nicht alle Quantenfelder physikalisch realisierbaren Operationen (nicht-observable Felder), doch lassen sich aus ihnen observable Grössen aufbauen. Die AQFT trägt dem Feldkonzept dadurch Rechnung, dass ein physikalisches System allein durch die Angabe der lokalen Observablen beschrieben wird: zu diesem Zweck ordnet man jedem Raum-Zeit-Gebiet die Algebra derjenigen Observablen zu, die in diesem Gebiet gemessen werden können; alle Observablen sind Grenzwerte von lokalen Observablen. Hierbei wird es vermieden, nicht-observable Felder zu betrachten, da diese selbst keiner Messung zugänglich sind.
bottom:.0001pt\'>Die lokalen Algebren können nicht unabhängig voneinander vorgegeben werden: zunächst muss natürlich die Algebra eines Gebietes die Algebren aller Teilgebiete enthalten (Isotonie). Darüberhinaus verlangt das Axiom der primitiven Kausalität, dass die Algebra eines Raum-Zeit-Gebietes von beliebig kleiner zeitlicher Ausdehnung alle zukünftigen Observablen enthält, deren kausale Vergangenheit von diesem Gebiet abgedeckt wird. Dadurch wird berücksichtigt, dass die Ausbreitungsgeschwindigkeit von dynamischen Prozessen durch die Lichtgeschwindigkeit begrenzt ist.
bottom:.0001pt\'>Die gegenseitige Beeinflussung von zwei physikalischen Operationen an einem System drückt sich in algebraischen Vertauschungsrelationen zwischen den zugehörigen Operatoren aus. Insbesondere müssen Observable, die in kausal unabhängigen Punkten der Raumzeit lokalisiert sind, durch kommutierende Operatoren beschrieben werden (Lokalität). Die über die Kodierung der Lokalität hinausgehende algebraische Struktur spezifiziert das physikalische System.
bottom:.0001pt\'>Anders als quantenmechanische Punktteilchen haben Quantenfelder unendlich viele Freiheitsgrade. Solche Systeme besitzen inäquivalente Darstellungen, d.h. verschiedene Realisierungen durch Hilbertraumoperatoren; deren Äquivalenzklassen werden als (Superauswahl-)Sektoren bezeichnet. Superauswahl-Sektoren sind ein globales Konzept: sie sind etwa durch eine "Gesamtladung des Universums" gekennzeichnet, die mit endlichem experimentellem Aufwand nicht gemessen werden kann. Daher ist es sinnvoll, das abstrakte System als algebraische Struktur zu betrachten; die (idealisiert angenommene) konkrete Präparation eines globalen Zustandes des Systems wird durch die Wahl einer Darstellung beschrieben, wobei nur wenige Darstellungen von physikalischem Interesse sind; diese gilt es durch geeignete Auswahl-Kriterien zu charakterisieren (s.u.).
bottom:.0001pt\'>Symmetrien
bottom:.0001pt\'>Wie überall in der Quantentheorie spielen Symmetrien eine wichtige Rolle. Äussere Symmetrien sind die Symmetrien der Raum-Zeit gemäss der Speziellen Relativitätstheorie; dagegen verbinden innere Symmetrien etwa Teilchen gleicher Masse, aber unterschiedlicher Ladung. Innere Symmetrien sind vor allem von phänomenologischer Relevanz.
bottom:.0001pt\'>Man muss zwischen der Symmetrie eines Systems (d.h. einem algebraischen Automorphismus) und ihrer Realisierung in einzelnen Zuständen unterscheiden. Es ist möglich, dass ein System eine Symmetrie besitzt, die in einer bestimmten Darstellung nicht durch einen implementierenden unitären Operator realisiert ("spontan gebrochen") ist. In der Regel setzt man die volle Invarianzgruppe der Speziellen Relativitätstheorie mit Ausnahme der Spiegelungen und Zeitumkehr als Raum-Zeit-Symmetrien der Algebra voraus, d.h. sowohl Translationen als auch die eigentlichen orthochronen Lorentz-Transformationen (Drehungen und Beschleunigungen). In teilchenartigen Zuständen, die zur Beschreibung von Streuprozessen studiert werden, ist die volle Symmetrie realisiert (mit Ausnahme von "Infrateilchen"), wodurch die verschwindende mittlere Energiedichte und endliche Gesamtladung charakterisiert wird; dagegen ist in thermischen Gleichgewichtszuständen (s.u.) die Lorentz-Symmetrie gebrochen.
bottom:.0001pt\'>Die AQFT beweist das Goldstone-Theorem, nach dem eine kontinuierliche Symmetrie nur dann spontan gebrochen sein kann, wenn die Darstellungen masselose Anregungen besitzen; im Gegensatz zu der ursprünglichen feldtheoretischen Herleitung ist der Gültigkeitsbereich dieses Gesetzes erweitert und gleichzeitig sehr genau abgegrenzt worden.
bottom:.0001pt\'>In einer translationskovarianten Darstellung kann man das Spektrum der Energie- und Impuls-Operatoren studieren. In physikalisch sinnvollen "teilchenartigen" Zuständen sollte das Spektrum nach unten beschränkt sein (Spektrumsbedingung), weil es nicht möglich ist, einem System von endlich vielen Teilchen beliebig viel Energie zu entziehen; interessanterweise reicht dann die Lorentz-Kovarianz der Algebra aus, um die Lorentz-Invarianz des "unteren Randes" des Spektrums zu beweisen, selbst wenn diese Symmetrie in der Darstellung gebrochen ist. Ist dieser untere Rand ein Punkt, so liegt ein Vakuumzustand vor; ein isoliertes Massenhyperboloid entspricht einem massiven Teilchen. Andere Möglichkeiten charakterisieren z.B. masselose Teilchen oder Infrateilchen. Von einer Massenlücke im Spektrum spricht man, wenn ausser dem Vakuum alle Anregungen eine Mindestmasse besitzen.
bottom:.0001pt\'>Im Gegensatz zu den teilchenartigen Zuständen kann einem unendlich ausgedehnten thermodynamischen System beliebig viel Energie entzogen werden; die Spektrumsbedingung ist für thermodynamische Darstellungen daher nicht angebracht. Die in der Quantenstatistik übliche Gibbssche Formulierung des kanonischen Ensembles mit Dichtematrizen ist wegen des kontinuierlichen Energiespektrums in unendlich ausgedehnten Systemen nicht möglich. An ihre Stelle tritt die sogenannte Kubo-Martin-Schwinger-(KMS)-Bedingung, die thermische Gleichgewichtszustände durch eine Analytizitätseigenschaft der dynamischen Korrelationsfunktionen auszeichnet.
bottom:.0001pt\'>Wie sich herausstellt, sind die lokalen Algebren einer relativistischen Quantenfeldtheorie vom Typ III (im von-Neumannschen Klassifikationsschema). Dies bedeutet, dass - im Gegensatz zu nichtrelativistischen Systemen - jeder Zustand lokal wie ein Mischungszustand aussieht; durch lokale Operationen kann ein globaler Zustand zwar mit beliebiger Genauigkeit approximiert werden, er bleibt jedoch (aufgrund der Quantenfluktuationen im Aussengebiet) stets von unendlich vielen anderen Zuständen ununterscheidbar.
bottom:.0001pt\'>Die globalen Raum-Zeit-Symmetrien sind (unter bestimmten Voraussetzungen) bereits durch die lokalen Algebren und den Vakuumzustand fixiert. Dieser Sachverhalt beruht auf einer Anwendung der "modularen Theorie" der abstrakten von-Neumann-Algebren vom Typ III, die zu jedem Zustand eine angepasste Dynamik konstruiert, bezüglich der er ein KMS-Zustand (s.o.) ist. Für bestimmte lokale Algebren im Vakuumzustand lässt sich diese Dynamik mit einer Untergruppe von Lorentz-Transformationen identifizieren. Dadurch wird es grundsätzlich möglich, die Spektrumsbedingung durch eine modulare Eigenschaft der Inklusion von lokalen Algebren zu geeigneten Gebieten zu charakterisieren. Darüberhinaus ergeben sich ein algebraischer Beweis des CPT-Theorems (Invarianz unter simultaner Raumspiegelung, Zeitumkehr und Ladungsumkehr) sowie neue Interpretationen des Unruh-Effekts und der Hawking-Strahlung schwarzer Löcher.
bottom:.0001pt\'>Eine Reihe von
spezifischen Annahmen betrifft die "Grösse" der lokalen
Observablenalgebren. So kann die Annahme, dass die Observablen in sich
berührenden kleinen Raum-Zeit-Gebieten die Algebra des Vereinigungsgebietes
erzeugen (Additivität), verwendet werden, um Theorien mit "fundamentalen
Längen" auszuschliessen. Thermodynamische Eigenschaften werden durch
Annahmen über die Grösse des Phasenraumes (Kompaktheit, Nuklearität) formuliert;
in engem Zusammenhang steht die Frage nach der unabhängigen Präparierbarkeit
von verschiedenen Zuständen auf kausal getrennten Gebieten
(Trennungs-Eigenschaft). Die AQFT beweist eine Vielzahl von logischen
Relationen zwischen diesen Annahmen und beispielsweise, der Form von
Massenspektren oder der quantitativen Verletzung der Bellschen Ungleichungen.
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Superauswahl-Sektoren
bottom:.0001pt\'>Von besonderer Bedeutung für die Theorie der Superauswahl-Sektoren ist die Eigenschaft der Haag-Dualität. Sie besagt, dass die lokalen Observablenalgebren durch Ad-hoc-Hinzunahme von weiteren Operatoren nicht vergrössert werden können, ohne das Kausalitätsaxiom zu verletzen. Je nachdem, für welche Gebiete Haag-Dualität verlangt wird, gibt es einfache und verschärfte Varianten. Die Gültigkeit der einfachen Varianten kann in vielen Modellen bewiesen werden. Ihre Verletzung ist ein Signal für spontan gebrochene Symmetrien.
bottom:.0001pt\'>Eine verschärfte Form dagegen kann in Modellen mit globalen, aber nicht lokalen Eichsymmetrien widerlegt werden. Die Möglichkeit, dass das Gausssche Gesetz in lokalen Eichtheorien sogar die verschärfte Haag-Dualität sicherstellt, und im Umkehrschluss diese Eigenschaft lokale Eichtheorien charakterisiert, ist von grossem Interesse.
bottom:.0001pt\'>Auf der Basis der einfachen Form der Haag-Dualität ist die Theorie der Superauswahl-Sektoren entwickelt worden. Diese führt zu einem allgemeinen Ladungsbegriff und erklärt die Gesetzmässigkeiten der Komposition von Ladungen. Dabei ergibt sich eine intrinsische Beschreibung der (Teilchen-) Statistik sowie ein feldunabhängiger Beweis des Spin-Statistik-Theorems, das die Bose-Einstein- bzw. Fermi-Dirac-Statistik mit der Ganz- bzw. Halbzahligkeit des Lorentz-Spins verknüpft. Das wichtigste Ergebnis dieser Theorie ist jedoch der Beweis eines Eichprinzips: alle "teilchenartigen" Superauswahl-Sektoren können durch nicht-observable lokalisierte Quantenoperatoren mit einer globalen (inneren) Eichsymmetrie aus dem Vakuumsektor erzeugt werden; die Eichinvarianten sind mit den ursprünglichen Observablen, und die Eichladungen mit den Superauswahl-Ladungen identisch. Die Algebra der "geladenen" Operatoren besitzt alle abstrakten Strukturen von Observablen mit der Ausnahme der Kausalität, die bei Anwesenheit von fermionischen Sektoren durch kausale Anti-Kommutativität zu ersetzen ist. Sie kann also selbst - als eine Erweiterung der gegebenen Observablentheorie - mit den Methoden der AQFT behandelt werden.
bottom:.0001pt\'>Die Klasse der teilchenartigen Sektoren, die in der Grundform dieser Theorie behandelt wird, wird durch ein scheinbar sehr einschränkendes Auswahlkriterium charakterisiert, das die Möglichkeit der Verschiebung von Ladungen in beliebig weit entfernte beschränkte Raum-Zeit-Gebiete ausdrückt. Es wurde jedoch gezeigt, dass alle massiven Zustände, die sich asymptotisch wie ein Vakuumzustand verhalten, zumindest die Konzentration von Ladungen in beliebig verschiebbaren und beliebig engen raumartigen Schläuchen zulassen. Diese Schläuche werden als Manifestation von "Gluonen-Strings" in nicht-abelschen Eichtheorien interpretiert.
bottom:.0001pt\'>Verschiedene Verallgemeinerungen
der Theorie der Superauswahl-Sektoren sind entwickelt worden. In integrablen
Modellen in einer räumlichen Dimension treten Soliton-Sektoren auf, die zwei
unterschiedliche Vakuumzustände asymptotisch verbinden. Niederdimensionale
Modelle sind nicht mehr durch die Fermi-Bose-Alternative eingeschränkt; das
Studium der möglichen Statistiken und deren Realisierung in konform-invarianten
Quantenfeldtheorien hat unerwartete Querverbindungen mit Gebieten der reinen
Mathematik (Knotentheorie und Theorie der Subfaktoren) aufgedeckt.
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Ausblick
bottom:.0001pt\'>Die AQFT befasst sich auch mit der Problematisierung des Teilchen-Begriffs. Dieser ist beispielsweise in der Quantenelektrodynamik nicht in der üblichen Form aufrechtzuerhalten, da etwa ein Elektron grundsätzlich nicht von der es umgebenden "Photonenwolke" zu trennen ist; die Quarks in der Quantenchromodynamik treten überhaupt nicht als isolierte Ladungsträger auf, da sie durch das Confinement stets aneinander gebunden bleiben. Die AQFT hat Konzepte entwickelt, um auch solche Teilchen zu erfassen.
bottom:.0001pt\'>Man nimmt an, dass die Teilchen-Problematik charakteristisch für lokale Eichtheorien ist. Diese Problematik ist damit auch nicht von der Schwierigkeit zu trennen, dass solche Theorien in allen ihren modernen Formulierungen notwendigerweise auf nicht-observable Felder zurückgreifen müssen, die keine Wahrscheinlichkeitsinterpretation im Sinne der Quantentheorie erlauben, und die damit den Rahmen der Anwendbarkeit der meisten mathematischen Lehrsätze der AQFT verlassen. Eine Charakterisierung von Eichtheorien anhand von algebraischen Eigenschaften allein ihrer Observablen sowie die anschliessende Analyse solcher Theorien mit den Methoden der AQFT ist noch nicht gelungen.
bottom:.0001pt\'>Das Begriffssystem der AQFT ist ohne weiteres auf Quantenfeldtheorien auf gekrümmten Raum-Zeiten, d.h. auf die semiklassische Allgemeine Relativitätstheorie, übertragbar. Allerdings können die meisten Resultate, die auf der Lorentz-Invarianz und der Spektrumsbedingung beruhen, nicht aufrechterhalten werden, da eine gekrümmte Raum-Zeit im allgemeinen keine globalen Symmetrien besitzt. Alternative Formulierungen, in denen lokale Eigenschaften an die Stelle der globalen Raum-Zeit-Symmetrien treten, sind ein aktueller Gegenstand der Forschung.
bottom:.0001pt\'>Eine echte
Quantengravitation im Rahmen der AQFT wird dagegen die absolute kausale
Struktur der Raum-Zeit aufgeben müssen, da diese in der Quantengravitation
selbst einer Heisenbergschen Unschärfe unterliegt.
character:
line-break\'>
character:line-break\'>
bottom:.0001pt\'>Literatur:
bottom:.0001pt\'>R. Haag, Local
Quantum Physics, Springer, New-York, Heidelberg, 2. Aufl. 1996.
H. Baumgärtel, M. Wollenberg, Causal Nets of Operator Algebras, Akademie
Verlag, Berlin, 1992.
N.N. Bogolubov, A.A. Logunov, I.T. Todorov, Axiomatic Quantum Field Theory,
Part VI, W.A. Benjamin, Reading, Mass., 1975.
D. Kastler (Hrsg.), The
Algebraic Theory of Superselection Sectors. Introduction and Recent Results,
World Scientific, Singapore, 1990.
N.P. Landsman: Local Quantum Physics, in: Stud. Hist. Phil. Mod.
Phys., Bd. 27, S. 511-524 (1996).
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>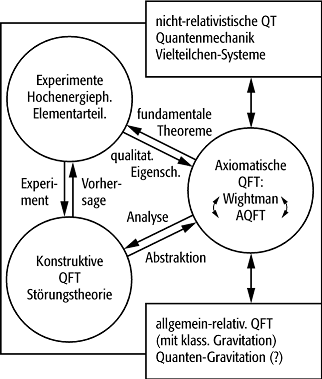
bottom:.0001pt;border:none; mso-border-left-alt:solid purple 1.5pt;mso-border-bottom-alt:solid purple 1.5pt; mso-border-right-alt:solid purple 1.5pt;padding:0cm;mso-padding-alt:0cm 13.0pt 13.0pt 13.0pt\'>Algebraische Quantenfeldtheorie: Die Stellung der AQFT in der Theorie (speziell-)relativistischer Quantenfelder.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.