Analytische Mechanik
Petra Nordinghaus-Martin
bottom:.0001pt\'>Die Mechanik ist eine zentrale Disziplin der Physik. Sie zeichnet sich wie kaum ein anderer Zweig durch einen grossen Reichtum an Formulierungen und Prinzipien aus und hat zahlreiche Verbindungen zu anderen Gebieten der Physik und der Technik. Für den Physiker teilt sich die nichtrelativistische Mechanik in die "Mechanik der Massenpunkte und starren Körper" und in die "Mechanik der Kontinua". Für den Maschinenbauer ist Mechanik "Technische Mechanik", die sich mit Elastostatik, Dynamik und vor allem mit der Statik beschäftigt.
bottom:.0001pt\'>Die analytische Mechanik ist eine theoretische Disziplin und behandelt die nichtrelativistische Mechanik der Massenpunkte und starren Körper in mathematischer Sprache. Als ihre Schöpfer dürfen in einer ersten Phase Galilei, Huygens und insbesondere Newton gelten. Die Weiterentwicklung des Formalismus im Sinne der eigentlichen Formulierung der analytischen Mechanik wurde hauptsächlich von D. Bernoulli, Euler, de Maupertius, d\'Alembert, Lagrange, Gauss, Hamilton und Jacobi betrieben.
bottom:.0001pt\'>Die drei Teilgebiete Newtonsche, Lagrangesche und Hamiltonsche Mechanik basieren auf denselben wenigen Axiomen und behandeln dieselbe Physik, arbeiten aber mit mathematisch völlig verschiedenen Formulierungen und haben daher verschiedene Stärken und Schwächen, in denen sich auch die historische Fortschreitung von der Newtonschen Mechanik über die Lagrangesche bis zur Hamiltonschen Formulierung und dem Konzept der kanonischen Transformationen widerspiegelt. Ferner unterscheiden sie sich in ihrer Zielsetzung und in ihrer Bedeutung für die Physik. Historisch betrachtet findet die lineare analytische Mechanik einen gewissen Endpunkt mit dem Noether-Theorem von 1918, das einen sehr allgemeinen Zusammenhang zwischen Symmetrien und Erhaltungsgrössen herstellt.
bottom:.0001pt\'>Die nichtlineare Dynamik erweitert das Gebäude der Mechanik um die Untersuchung chaotischer Bewegungsformen. Dieser Zweig der Mechanik hat in kurzer Zeit eine solche Bedeutung entwickelt, dass er allgemein als eigenständiges Teilgebiet der Physik betrachtet wird. Die Entwicklung der linearen analytischen Mechanik kann demgegenüber heute als abgschlossen gelten.
bottom:.0001pt\'>Einen Überblick über die analytische Mechanik - und damit auch über den Inhalt dieses Beitrages - soll die Abbildung geben.
bottom:.0001pt\'>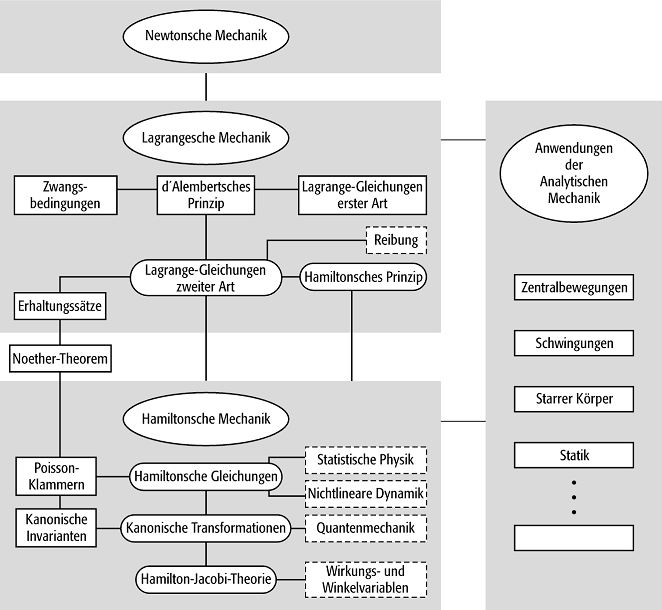
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Analytische Mechanik: Gliederungsschema.
bottom:.0001pt\'>Die Newtonsche Mechanik
bottom:.0001pt\'>Die Newtonsche Mechanik
beruht im wesentlichen auf den drei Newtonschen Axiomen, die Newton im Jahre
1687 in seinen "Philosophiae naturalis principia mathematica"
veröffentlichte. Die zentrale Bewegungsgleichung der Newtonschen Mechanik ist
das zweite Newtonsche Axiom 
, eine Differentialgleichung,
die den Zusammenhang zwischen der Kraft F auf einen Massenpunkt m
und der Beschleunigung 
des Massenpunktes beschreibt. Es gilt in
Inertialsystemen, deren Existenz durch das erste Newtonsche Axiom postuliert
wird, und nur für konstante Massen m (wie überall in diesem Beitrag).
Die Lösung r(t) der Bewegungsgleichung beschreibt die Bahn
des Massenpunktes. Die konsequente Anwendung seiner Axiome erlaubte Newton, die
Keplerschen Gesetze aus dem Newtonschen Gravitationsgesetz abzuleiten sowie den
freien Fall mathematisch zu beschreiben. Die überragende Bedeutung von Newtons
Werk liegt darin, dass seine Axiome zum ersten Mal in der Geschichte der
Naturwissenschaft ein mathematisches Fundament lieferten, mit dessen Hilfe
Beobachtungen und Experimente rechnerisch nachzuvollziehen waren.
bottom:.0001pt\'>Ein wesentlicher Vorteil der Newtonschen Mechanik aus heutiger Sicht ist ihre Anschaulichkeit, die sich beispielsweise in der elementaren Verwendung der Begriffe Kraft und Drehmoment ausdrückt, die für Maschinenbauer von zentraler Bedeutung sind; die Lagrangesche und die Hamiltonsche Mechanik sind, daran gemessen, wesentlich abstrakter formuliert. Dem stehen zwei gravierende Nachteile der Newtonschen Mechanik gegenüber:
bottom:.0001pt\'>-Zur Beschreibung der Bewegung von Systemen mit Zwangsbedingungen müssen die Zwangskräfte mühsam berechnet werden, obwohl sie selbst meist nicht von Interesse sind. Die Aufstellung der Bewegungsgleichungen ist daher oft schwierig.
bottom:.0001pt\'>-Beim Übergang von
kartesischen Koordinaten auf krummlinige Koordinaten und von inertialen auf
beschleunigte Bezugssysteme - diese Übergänge werden durch
Punkttransformationen der Koordinaten 
beschrieben - sind die Bewegungsgleichungen 
nicht forminvariant; vielmehr müssen die
Beschleunigungen auf die neuen Koordinaten Xi umgerechnet werden,
so dass die Gleichungen eine andere Gestalt annehmen
bottom:.0001pt\'>
Die Lagrangesche Mechanik
bottom:.0001pt\'>Die Epoche nach Newton, die den Grundlagen der Mechanik nichts grundsätzlich Neues hinzufügte, war durch das Bemühen charakterisiert, einerseits die mathematische Seite der Theorie zu durchdringen, um die Schwierigkeiten der Newtonschen Mechanik umgehen zu können, und andererseits Prinzipien aufzufinden, die als der Mechanik übergeordnet angesehen werden konnten, um so einen geschlossenen, auf wenigen allgemeinen Axiomen beruhenden Formalismus entwickeln zu können.
bottom:.0001pt\'>In der gegenüber der Newtonschen Formulierung stärker abstrahierten Lagrangeschen Mechanik, deren Prinzipien J.-L. Lagrange in seiner "Mécanique analytique" von 1788 darlegte, entfallen die zwei gravierenden Nachteile der Newtonschen Mechanik. Kernstück der Lagrangeschen Mechanik sind die Lagrange-Gleichungen zweiter Art:
bottom:.0001pt\'>
bottom:.0001pt\'>Hierin ist 
(T = kinetische, V = potentielle
Energie) die Lagrange-Funktion, die für ein System von N Massenpunkten
mit k holonomen, also durch Bedingungsgleichungen der Koordinaten und
der Zeit 
formulierbaren Zwangsbedingungen, von 3N - k
verallgemeinerten Koordinaten qi abhängt. Die Wahl der verallgemeinerten
Koordinaten, deren Anzahl der Zahl der Freiheitsgrade des Systems entspricht,
ist dabei nicht eindeutig; eine geeignete Wahl zu treffen, ist wichtig, um eine
möglichst einfache Gestalt der Bewegungsgleichung zu erhalten.
bottom:.0001pt\'>Es handelt sich bei den Lagrange-Gleichungen zweiter Art, die oft auch einfach als Lagrange-Gleichungen bezeichnet werden, um einen Satz von 3N - k Differentialgleichungen zweiter Ordnung. Die Wichtigkeit dieser Gleichungen kann kaum überschätzt werden. Sie bilden den Ausgangspunkt der formalen Weiterentwicklung der Mechanik, und aufgrund ihrer Einfachheit und Forminvarianz unter Punkttransformationen sowie der geradezu idealen Anpassung an holonome Nebenbedingungen eignen sie sich von allen Prinzipien und Formalismen in der Regel am besten zur Aufstellung von Bewegungsgleichungen.
bottom:.0001pt\'>Von viel geringerer Bedeutung sind die Lagrange-Gleichungen erster Art, obwohl sie auch für Systeme mit differentiellen Zwangsbedingungen gelten und Zwangskräfte relativ einfach berechnen.
bottom:.0001pt\'>Die Ableitung der
Lagrange-Gleichungen beruht neben dem zweiten Newtonschen Axiom auf dem
d\'Alembertschen Prinzip der virtuellen Verrückung, dem zufolge die
Zwangskräfte, die Kräfte also, die ein System zur Einhaltung der
Nebenbedingungen zwingen, keine Arbeit verrichten. Dieses Prinzip kann nicht
aus der Newtonschen Mechanik abgeleitet werden, muss also als ein neues, auf der
Erfahrung beruhendes Prinzip in die Physik eingeführt werden. Die Erfahrung, die
hinter diesem Prinzip steckt, ist die, dass beispielsweise das Gestänge einer
Dampfmaschine selbst keine Arbeit leistet, sondern lediglich Kräfte überträgt.
Durch die Anwendung des d\'Alembertschen Prinzips verschwinden die Zwangskräfte
aus den Gleichungen.
character:line-break\'>
character:line-break\'>
bottom:.0001pt;background:silver;
mso-shading:windowtext;mso-pattern:solid silver\'>Ein Beispiel, das die
Schwierigkeiten der Newtonschen Mechanik illustrieren kann, ist das
Fadenpendel, also eine in festem Abstand von einem Drehpunkt aufgehängte
Punktmasse. Das erste Problem bei der Aufstellung der Bewegungsgleichung tritt
auf, wenn man von den üblichen kartesischen Koordinaten zu Polarkoordinaten
übergehen will. Polarkoordinaten sind dem Problem des Fadenpendels besser
angepasst, jedoch hat das zweite Newtonsche Axiom in ebenen Polarkoordinaten
nicht die oben angegebene Gestalt; es lautet jetzt: 
. Die zweite,
weitaus problematischere Schwierigkeit ist die Berechnung der resultierenden
Kraft, die auf die Masse wirkt, denn diese Kraft umfasst neben der Schwerkraft
auch die Zwangskraft, die der Faden auf die Masse ausübt; letztere ist etwas mühsam
zu bestimmen, da sie neben der Schwerkraft auch die Zentrifugalkraft der
Pendelschwingung kompensieren muss. Der Weg zur Bewegungsgleichung ist also
recht umständlich, wenn man nicht die Energieerhaltung ausnutzt.
bottom:.0001pt\'>
bottom:.0001pt\'>Erhaltungsgrössen und das Noether-Theorem
bottom:.0001pt\'>Das grösste Problem bei der Untersuchung mechanischer Systeme ist oft nicht die Aufstellung der Bewegungsgleichungen, die in Form der Lagrange-Gleichungen des betrachteten Systems in vielen Fällen sehr einfach niedergeschrieben werden können, sondern ihre Lösung. Leider ist eine analytische Lösung der Bewegungsgleichungen nur in seltenen Fällen möglich. Erhaltungsgrössen helfen hier einen entscheidenden Schritt weiter bei dem Versuch, auch ohne Integration Kenntnisse über das Verhalten der untersuchten Systeme zu gewinnen: Sie liefern wesentliche Informationen ohne Lösung der Bewegungsgleichungen. Zudem erniedrigt jede Erhaltungsgrösse die Zahl der Integrationen, die zur Lösung der Bewegungsgleichungen erforderlich sind, um Eins; die Lösung wird also in vielen Fällen einfacher.
bottom:.0001pt\'>Jedes abgeschlossene mechanische System weist sieben fundamentale Erhaltungsgrössen, die sogenannten Bewegungsintegrale, auf, nämlich die Energie sowie die je drei Komponenten des Impulses und des Drehimpulses. Diese Erhaltungssätze haben ihre tiefere Ursache in einer räumlich-zeitlichen Symmetrie des Systems, nämlich in der Invarianz gegenüber einer beliebigen zeitlichen und räumlichen Translation und einer beliebigen räumlichen Drehung.
bottom:.0001pt\'>Der Zusammenhang zwischen Symmetrien des Systems und Erhaltungssätzen lässt sich zu der Erkenntnis erweitern, dass jede kontinuierliche Koordinatentransformation, die die Lagrange-Funktion invariant lässt, auf eine Erhaltungsgrösse hinweist und deren einfache Berechnung ermöglicht. Dies findet seine Formulierung im 1918 von A.E. Noether und D. Hilbert abgeleiteten Noether-Theorem, dem zufolge die Funktion
bottom:.0001pt\'>
bottom:.0001pt\'>erhalten ist, wenn die
Lagrange-Funktion Invarianz unter einer kontinuierlichen
Koordinatentransformation zeigt; die Transformation wird dabei durch den stetig
differenzierbaren Parameter a gemäss 
definiert. Zu jeder solchen
Symmetrietransformation gehört also eine Erhaltungsgrösse.
bottom:.0001pt;background:silver;
mso-shading:windowtext;mso-pattern:solid silver\'>Anhand des Fadenpendels, das
bereits oben als Beispiel diente, lässt sich die perfekte Anpassung des
Lagrange-Formalismus an holonome Zwangsbedingungen zeigen. In einem ersten
Schritt wählt man geeignete unabhängige Koordinaten, das ist bei einem ebenen
Pendel der Fadenlänge l nur der Winkel j, und berechnet unter
Verwendung der Erdbeschleunigung g die Lagrange-Funktion zu
.
Daraus ergibt sich dann die Lagrange-Gleichung 
, die mit der
für kleine Auslenkungen zulässigen Näherung 
unmittelbar gelöst werden kann. Das Problem
der Zwangskräfte stellt sich nicht, da diese in den Lagrange-Gleichungen
prinzipiell nicht auftreten.
bottom:.0001pt\'>
bottom:.0001pt\'>Wichtige Anwendungen der analytischen Mechanik
bottom:.0001pt\'>Die meisten elementaren Anwendungen der Mechanik werden wegen der oben beschriebenen Vorteile bevorzugt auf der Basis des Lagrangeschen Formalismus behandelt.
bottom:.0001pt\'>Eine historisch in der Enwicklung der Mechanik zentrale Anwendung ist die Zentralkraftbewegung, die Bewegung eines Körpers in einem Zentralfeld. Es war einer der grossen Erfolge der Newtonschen Mechanik, Keplers empirisch gefundene Gesetze der Planetenbewegung auf das Gravitationsgesetz und das zweite Newtonsche Axiom zurückführen zu können. Die Zentralkraftbewegungen sind auch aus heutiger Sicht von herausragender Bedeutung für die Mechanik, da sie zu den wenigen Aufgaben gehören, die analytisch exakt gelöst werden können. Die Behandlung im Rahmen des Lagrangeschen Formalismus bringt hier gegenüber der Newtonschen Betrachtung den Vorteil, dass die Bewegungsgleichungen durch leichteres Auffinden der Erhaltungsgrössen einfacher zu integrieren sind.
bottom:.0001pt\'>Der starre Körper zählt zu den faszinierendesten Objekten der Mechanik; besonders die Theorie des Kreisels, die vielfach als die "Hohe Schule der Mechanik" angesehen wird, zeigt immer wieder verblüffende Effekte. Die Berechnung von Trägheitsmomenten starrer Körper und die Untersuchung von Drehbewegungen, rotierenden Maschinenteilen und Unwuchten sind auch für Ingenieure wichtig.
bottom:.0001pt\'>Schwingungen sind ein
zentrales Thema auf vielen Gebieten der Physik. Die Schwingungslehre ist für
Naturwissenschaftler und Ingenieure unentbehrlich und gehört zu den Grundlagen
der technischen Mechanik und der Elektrotechnik. Der harmonische Oszillator ist
schlechthin das wichtigste Modellsystem der Physik überhaupt, dies einerseits,
weil der harmonische Oszillator gleich der Zentralkraftbewegung zu den ganz
wenigen analytisch exakt lösbaren Aufgaben gehört, und andererseits, weil viele
in der Natur vorkommende Systeme näherungsweise als harmonische Oszillatoren
betrachtet und so ihre Bewegungsgleichungen gelöst werden können.
character:line-break\'>
character:line-break\'>
bottom:.0001pt;background:silver;
mso-shading:windowtext;mso-pattern:solid silver\'>Beim Beispiel des ebenen
Pendels ist der zentrale Erhaltungssatz derjenige der Energie, dem zufolge die
Summe aus kinetischer und potentieller Energie konstant ist. Legt man
insbesondere den Nullpunkt der potentiellen Energie des Schwerefeldes in den
tiefsten Punkt der Pendelschwingung, so muss die kinetische Energie in diesem
Punkt der potentiellen Energie in den Wendepunkten der Bewegung entsprechen, in
denen die kinetische Energie verschwindet: 
. Man erhält so
direkt Informationen über die maximale Auslenkung und die Geschwindigkeit im
tiefsten Punkt der Schwingung. Es ist nun auch möglich, mittels der allgemeinen
Form der Energieerhaltung 
die Ableitung des Winkels 
durch die Energie E und den Winkel j
auszudrücken und dies in die Lagrange-Gleichung einzusetzen, die dadurch von
einer Gleichung zweiter zu einer Gleichung erster Ordnung in der Zeitableitung
wird. Die Zahl der Integrationen zur Lösung der Gleichung verringert sich dann
von Zwei auf Eins. Auf solchen Informationen beruht zu einem grossen Teil die
Bedeutung der Erhaltungsgrössen für die Mechanik.
bottom:.0001pt\'>
bottom:.0001pt\'>Das Prinzip der kleinsten Wirkung
bottom:.0001pt\'>Statt aus der Newtonschen Mechanik unter Verwendung des D\'Alembert-Prinzips kann die Lagrangesche Mechanik auch aus einem einzigen grundlegenden Axiom, dem Hamiltonschen Prinzip der kleinsten Wirkung entwickelt werden. Dieses 1823 von W.R. Hamilton aufgestellte Variationsprinzip geht nicht wie das D\'Alembert-Prinzip von virtuellen Verrückungen des momentanen Zustandes aus, sondern stellt eine Extremalforderung an die gesamte Bewegung zwischen den Zeiten t1 und t2, die derart verlaufen soll, dass die Wirkung S extremal, in der Regel minimal wird; anders ausgedrückt, dass die erste Variation der Wirkung
bottom:.0001pt\'>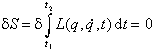
bottom:.0001pt\'>oder, ausgeschrieben
bottom:.0001pt\'>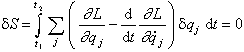
bottom:.0001pt\'>verschwindet. Dabei sind dqj Variationen der Koordinate qj zur Zeit t. Das Hamiltonsche Prinzip gilt für alle Systeme, die holonomen oder differentiellen Zwangsbedingungen unterworfen sind, und für Kräfte, die aus einem geschwindigkeitsabhängigen Potential abgeleitet werden können. Es ist äquivalent zu den Lagrange-Gleichungen zweiter Art.
bottom:.0001pt\'>Für die Lösung konkreter mechanischer Aufgaben bietet sich das Hamiltonsche Prinzip nicht an. Seine Bedeutung beruht vielmehr auf folgenden Punkten:
bottom:.0001pt\'>-Es enthält über die Lagrange-Funktion L = T - V nur die kinetische und potentielle Energie und hat daher eine von der Wahl der Koordinaten unabhängige Bedeutung. Daher wird es gerne bei der Untersuchung von Transformationen der Variablen verwendet.
bottom:.0001pt\'>-Das Prinzip der kleinsten Wirkung gehört zu den allgemeinen Prinzipien der Physik; es tritt auch in anderen Gebieten auf und führt z.B. auf die Wellengleichung. Damit ist es gelungen, die gesamte Mechanik auf ein einziges sehr allgemeines Prinzip zurückzuführen.
bottom:.0001pt\'>Ein axiomatisch
aufgebautes Bild der analytischen Mechanik kann daher das Hamiltonsche Prinzip
als grundlegendes Axiom betrachten, um von dort aus die Lagrangesche Mechanik
zu entwickeln; von diesem strengen theoretischen Blickwinkel aus ist die
Newtonsche Formulierung der Prinzipien der Mechanik heute hauptsächlich von
historischem Interesse.
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Die Hamiltonsche Mechanik
bottom:.0001pt\'>Die Bewegungsgleichungen der Newtonschen und der Lagrangeschen Mechanik sind von zweiter Ordnung in der Zeit; eine alternative Formulierung der Mechanik, deren Bewegungsgleichungen von erster Ordnung in der Zeit sind, liefert die Hamiltonsche Mechanik.
bottom:.0001pt\'>Während die beiden
älteren Darstellungen im n-dimensionalen Raum der unabhängigen
Koordinaten qj,
dem Konfigurationsraum, formuliert sind, ist der Raum der Hamiltonschen
Mechanik der 2n-dimensionale Phasenraum, der durch die unabhängigen
Koordinaten qj
und zusätzlich durch die von den Koordinaten unabhängigen kanonischen Impulse 
aufgespannt wird.
bottom:.0001pt\'>Die Hamilton-Funktion H wird gemäss
bottom:.0001pt\'>
bottom:.0001pt\'>über die
Lagrange-Funktion eingeführt. (Mathematisch handelt es sich bei dieser
Koordinatentransformation von den Geschwindigkeiten 
zu den Impulsen pi um eine
Legendre-Transformation.) In der Regel - präziser: im Falle skleronomer,
holonomer Zwangsbedingungen, ruhender Koordinaten und konservativer Kräfte -
kann H mit der Energie E des Systems idendifiziert werden. Die
Berechnung des totalen Differentials dH liefert die Bewegungsgleichungen
der Hamiltonschen Mechanik, die Hamiltonschen Gleichungen:
bottom:.0001pt\'>
bottom:.0001pt\'>sowie die Gleichung
bottom:.0001pt\'>
bottom:.0001pt\'>Die Hamiltonschen Gleichungen sind 2n explizite Differentialgleichungen erster Ordnung in den Koordinaten und kanonischen Impulsen. Wegen ihrer formalen Einfachheit und Symmetrie heissen sie auch kanonische Gleichungen. Die Hamiltonschen Gleichungen sind, gleich den Lagrange-Gleichungen, äquivalent zum Hamiltonschen Variationsprinzip, beschreiben also die gleiche Physik.
bottom:.0001pt\'>Da die 2n Hamiltonschen Gleichungen eines mechanischen Systems im allgemeinen nicht einfacher aufzustellen und zu lösen sind als die n Lagrange-Gleichungen zweiter Art - der Lösungsweg ist, zumindet bei einfachen Problemen, sogar eher umständlicher -, haben sie im Vergleich zu letzteren für die Lösung mechanischer Aufgaben nur geringe Bedeutung. Ihre äusserst grosse Wichtigkeit für die Physik beruht auf folgenden Punkten:
bottom:.0001pt\'>-Die Hamiltonsche Mechanik ist der Ausgangspunkt für die Formulierung der Quantenmechanik. Der Übergang wird vollzogen, indem die Koordinaten und die kanonischen Impulse durch entsprechende Operatoren ersetzt werden, die auf die Wellenfunktion wirken; die Hamilton-Funktion der Mechanik wird so zum Hamilton-Operator der Quantentheorie.
bottom:.0001pt\'>-Die Hamiltonschen
Gleichungen sind Differentialgleichungen im Phasenraum. Sie bilden daher die
Grundlage der statistischen Mechanik, die als Mechanik bei sehr grossen
Teilchenzahlen im Phasenraum entwickelt wird. Die Hamiltonschen Gleichnungen
werden auch gerne für qualitative, geometrische Beschreibungen der Bewegung in
chaotischen Systemen verwendet.
character:line-break\'>
character:line-break\'>
bottom:.0001pt\'>Die Poisson-Klammern
bottom:.0001pt\'>Das Konzept der Poisson-Klammern stellt eine Weiterentwicklung auf der Basis des Hamilton-Formalismus dar, die besonders für den oben erwähnten Übergang von der Mechanik zur Quantenmechanik von grosser Bedeutung ist.
bottom:.0001pt\'>Wenn f(q,p,t) und g(q,p,t) zwei beliebige differenzierbare Funktionen der Koordinaten, der Impulse und der Zeit sind - solche Grössen heissen Observablen, da sie gewöhnlich einer Messgrösse entsprechen -, werden die Poisson-Klammern dieser Observablen in der Form
bottom:.0001pt\'>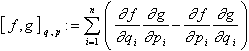
bottom:.0001pt\'>definiert. Es lässt sich leicht zeigen, dass man mit Hilfe dieser Klammern die totale Zeitableitung einer Observablen f gemäss
bottom:.0001pt\'>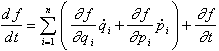
bottom:.0001pt\'>
bottom:.0001pt\'>in einfacher Form schreiben kann, und die kanonischen Gleichungen lauten dann gleichfalls sehr einfach
bottom:.0001pt\'>
und 
.
bottom:.0001pt\'>In diesem Zusammenhang, auch im Hinblick auf die kanonischen Transformationen, werden die unabhängigen Koordinaten und die kanonischen Impulse als kanonisch konjugierte Variablen bezeichnet.
bottom:.0001pt\'>Die Poisson-Klammern
haben die gleiche algebraische Struktur wie die Operatoren der Quantenmechanik
bzw. deren Kommutatoren und eröffnen daher die Möglichkeit, die Quantenmechanik
- genauer: die Heisenbergsche Matrizenmechanik - analog der analytischen
Mechanik aufzubauen: In oben angegeben Form entsprechen die kanonischen
Gleichungen denjenigen der Matrizenmechanik, wobei der Kommutator zweier
Operatoren die Stelle der Poisson-Klammer der klassischen Mechanik einnimmt.
character:line-break\'>
character:line-break\'>
bottom:.0001pt;background:silver;
mso-shading:windowtext;mso-pattern:solid silver\'>Es sei an dieser Stelle
nochmals das Beispiel des ebenen Pendels aufgegriffen: Der zum Winkel j
gehörige kanonische Impuls ist 
. Damit
berechnet sich die Hamilton-Funktion zu 
;
H entspricht damit genau der Summe aus kinetischer und potentieller
Energie. Die kanonischen Gleichungen lauten 
und 
; dieses
Gleichungssystem kann, wiederum unter Verwendung der Näherung 
, integriert
werden. Man erhält also im Hamilton-Formalismus zwei Gleichungen erster Ordnung
statt einer einzigen von zweiter Ordnung im Lagrange-Formalismus.
bottom:.0001pt\'>
bottom:.0001pt\'>Die Hamilton-Jacobi-Theorie der kanonischen Transformationen
bottom:.0001pt\'>Im Rahmen der Hamilton-Jacobi-Theorie, gleichfalls eine Weiterentwicklung der Hamiltonschen Mechanik, wird die Lösung einer speziellen Klasse von Problemen, der separierbaren Aufgaben, auf die Berechnung eindimensionaler Integrale zurückgeführt, die im allgemeinen einfacher auszuführen sind als die Lösung der gekoppelten Gleichungssysteme des Lagrange- oder des Hamilton-Formalismus. Am Anfang der Hamilton-Jacobi-Theorie steht die Betrachtung der sogenannten kanonischen Koordinatentransformationen:
bottom:.0001pt\'>Die Hamiltonsche Mechanik hat 2n unabhängige und völlig gleichberechtigte Variablen qi, pi. Daher können erweiterte Transformationen der Koordinaten und Impulse
bottom:.0001pt\'>
bottom:.0001pt\'>untersucht werden. Unter diesen unzähligen erdenklichen Transformationen sind nicht alle von Interesse, sondern nur diejenigen, die die kanonischen Gleichungen unverändert lassen. Es muss also auch in den neuen Variablen eine Hamilton-Funktion K(Q,P,t) existieren, mit der die kanonischen Gleichungen die bekannte Form annehmen:
bottom:.0001pt\'>
bottom:.0001pt\'>Die kanonischen Transformationen bilden die massgebliche Teilmenge dieser brauchbaren Transformationen. Sie werden durch Funktionen, sogenannte Erzeugende, gekennzeichnet, die von den alten (qi, pi) und den neuen Variablen (Qi, Pi) sowie von der Zeit abhängen. Eine Transformation, bei der z.B. die 2n Variablen pi, Pi unabhängig voneinander sind, ist genau dann kanonisch, wenn eine Erzeugende F(q,P,t) existiert mit den Transformationsgleichungen
bottom:.0001pt\'>
bottom:.0001pt\'>Die kanonischen Transformationen liefern neue Einsichten und Formulierungen der Mechanik und führen unter anderem zur Hamilton-Jacobi-Theorie, zu den Winkel- und Wirkungsvariablen, zur statistischen Mechanik und zur Schrödingerschen Wellenmechanik.
bottom:.0001pt\'>Die
Hamilton-Jacobi-Theorie sucht kanonische Transformationen auf Variablen, die
Erhaltungsgrössen sind: 
. Eine solche
Transformation ist gefunden, wenn die neue Hamilton-Funktion K - und mit
ihr auch die Poisson-Klammern 
und 
- verschwinden. Es ergibt sich also die
Bedingungsgleichung
bottom:.0001pt\'>
bottom:.0001pt\'>Von den 3n
Variablen qi,
pi,
Pi
- von der Zeit wird abgesehen - sind aufgrund der Transformationsgleichungen
nur 2n unabhängig voneinander. Ersetzt man die Impulse pi durch 
, so erhält man
die Hamilton-Jacobi-Gleichung
bottom:.0001pt\'>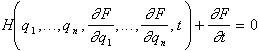
bottom:.0001pt\'>Die
Hamilton-Jacobi-Gleichung ist eine nichtlineare, partielle
Differentialgleichung erster Ordnung in den Variablen 
für die Erzeugende F(q,P,t)
einer kanonischen Transformation auf konstante Variable Qi, Pi . Nach der
Berechnung der Erzeugenden ergeben sich die neuen Variablen aus den
Transformationsgleichungen.
bottom:.0001pt\'>Im allgemeinen ist die Hamilton-Jacobi-Gleichung nur dann lösbar, wenn die Variablen separiert werden können. Dann aber ist das System integrabel, d.h. die Lösung ist auf eindimensionale Integrale rückführbar und wird so verhältnismässig leicht durchführbar.
bottom:.0001pt\'>Wie das Beispiel zeigt, ist die Hamilton-Jacobi-Theorie bei einfachen Aufgaben recht schwerfällig (siehe Randspalte); ihre Vorzüge kommen erst in schwierigeren Problemen, so zum Beispiel bei der Überlagerung eines Zentralkraftfeldes mit einem homogenen Feld oder beim Zweizentrenproblem voll zur Geltung. Es gibt auch Probleme, die nur mit der Hamilton-Jacobi-Theorie exakt gelöst werden können.
bottom:.0001pt\'>Die Ähnlichkeit
zwischen der Hamilton-Jacobi-Gleichung und der Eikonalgleichung der
geometrischen Optik führte E. Schrödinger im Jahre 1926 zur Aufstellung der zeitunabhängigen
Schrödinger-Gleichung.
character:line-break\'>
character:line-break\'>
bottom:.0001pt;background:silver;
mso-shading:windowtext;mso-pattern:solid silver\'>Beim Beispiel des ebenen
Pendels kann die Hamilton-Funktion näherungsweise als 
geschrieben werden. Die
Hamilton-Jacobi-Gleichung des Systems ist daher 
Mittels des Ansatzes 
mit dem freien Parameter a wird die Zeit
separiert, man erhält die Gleichung 
,
die die Zeit nicht mehr enthält. Der Parameter a entspricht
offensichtlich der Energie E. Damit ist die Lösung leicht zu 
zu finden.
bottom:.0001pt\'>
bottom:.0001pt\'>Ausblick auf die nichtlineare Dynamik
bottom:.0001pt\'>Es ist ein Irrtum anzunehmen, dass die überwiegende Anzahl der Systeme der klassischen Mechanik analytisch gelöst werden kann, und dass die Lösung dann reguläres Verhalten zeigt. Bereits 1892 hat Poincaré erkannt, dass das nicht integrierbare Dreikörperproblem unter Umständen chaotisches Verhalten zeigen kann. Kolmogorow (1954), Arnold (1963) und Moser (1967) bewiesen in ihrem berühmten KAM-Theorem, dass es in empfindlicher Weise von den Anfangsbedingungen eines klassischen Systems abhängt, ob seine Bewegung regulär oder chaotisch verläuft; es zeigte sich, dass die klassische stabile, reguläre Bewegung eine Ausnahme darstellt, die in der Natur nur selten in reiner Form realisiert ist. Die Untersuchung solcher zu irregulärem Verhalten tendierender Systeme ist Gegenstand der nichtlinearen Dynamik (Chaos), die im Prinzip als eine Erweiterung der klassischen Mechanik verstanden werden kann; tatsächlich jedoch haben sich in diesem bedeutenden Bereich, der in einer stürmischen Entwicklung begriffen ist, in solchem Masse eigene Methoden ausgebildet, dass er meist als ein eigenständiger Zweig der Physik gilt.
bottom:.0001pt;border:none;mso-border-left-alt: solid purple 1.5pt;mso-border-bottom-alt:solid purple 1.5pt;mso-border-right-alt: solid purple 1.5pt;padding:0cm;mso-padding-alt:0cm 13.0pt 13.0pt 13.0pt\'>Die Entwicklung der klassischen, nichtrelativistischen, linearen analytischen Mechanik hingegen kann heute als weitgehend abgeschlossen betrachtet werden; ihre Prinzipien haben sich jedoch auf fast allen Gebieten der Physik bewährt. Neben der nichtlinearen Dynamik dürfen besonders die Quantenmechanik und die statistische Physik in diesem Sinne als moderne Weiterentwicklungen der klassischen Mechanik angesehen werden.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.